Coursera-吴恩达-机器学习-第六周-编程作业: Regularized Linear Regression and Bias/Variance
本次文章内容: Coursera吴恩达机器学习课程,第六周编程作业。编程语言是Matlab。
学习算法分两部分进行理解,第一部分是根据code对算法进行综述,第二部分是代码。
0 Introduction
在这个练习中,应用regularized linear regression,并观察其bias-variance properties性质。
1 Regularized Linear Regression and Bias v.s. Variance
Part 0 Initialization
clear ; close all; clc。常规操作。
Part 1: Loading and Visualizing Data
可视化test data。
Part 2: Regularized Linear Regression Cost && Linear Regression Gradient
计算cost function 和 gradient ,注意, 正则化不包含第0项,所以从0开始。
Part 4: Train Linear Regression
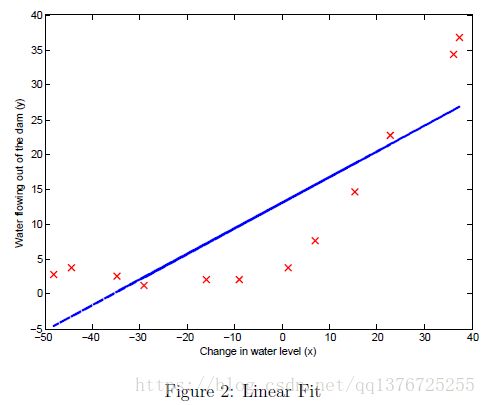
run the code in trainLinearReg(),计算the optimal values θ。并画出Linear Regression图像,从图中可以观察是high bias 的情况。
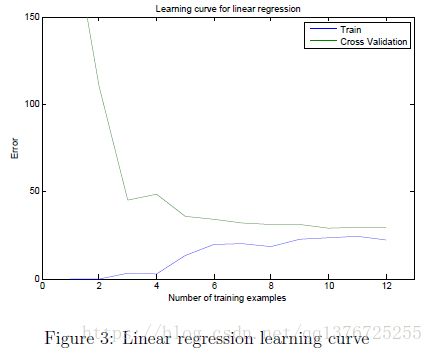
Part 5: Learning Curve for Linear Regression
先计算得到的theta值,用theta值计算test误差和cross validation误差,注意 计算the training error 时不包含the regularization term,单纯计算误差就好。
画出Learning curves图像。
Part 6: Feature Mapping for Polynomial Regression
使用Polynomial Regression的hypothesis,另外注意需要做 feature normalization,因为坐标会被缩放至k度。从图中可以观察是high variance的情况。
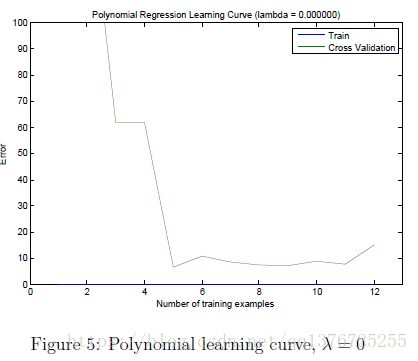
Part 7: Learning Curve for Polynomial Regression
画出 Polynomial Regression的Learning curves图像。
Part 8: Validation for Selecting Lambda
当 λ =1时,Polynomial Regression和Learning curves图像:
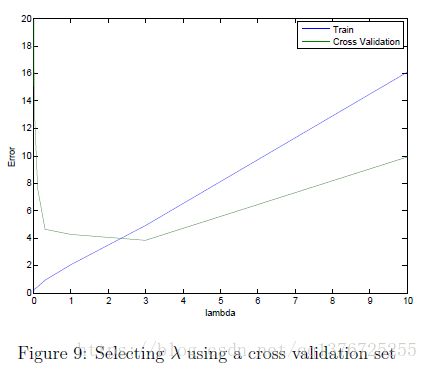
Selecting λ using a cross validation set,画出随λ 变化的图像,选择最佳的方案。如图可以知道最佳在value 3 附近。
2. code
function [J, grad] = linearRegCostFunction(X, y, theta, lambda),函数部分中添加:
J = 1/2/m* sum((X*theta - y) .^ 2) + lambda/2/m * sum(theta(2:end) .^ 2);
grad = 1/m* (X'*(X*theta - y));
grad(2:end) = grad(2:end) + lambda/m*theta(2:end);function [error_train, error_val] = learningCurve(X, y, Xval, yval, lambda) ,函数部分中添加:
for i=1:m
theta = trainLinearReg(X(1:i, :), y(1:i), lambda);
error_train(i) = linearRegCostFunction(X(1:i, :), y(1:i), theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
endfunction [X_poly] = polyFeatures(X, p) ,函数部分中添加:
for i = 1:p
X_poly(:,i) = X.^i;
end
function [lambda_vec, error_train, error_val] = validationCurve(X, y, Xval, yval) , 函数部分中添加:
for i=1:size(lambda_vec, 1)
theta = trainLinearReg(X, y, lambda_vec(i));
error_train(i) = linearRegCostFunction(X, y, theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end