凸集的定义:
设集合 D⊂Rn D ⊂ R n ,若对于任意点 x,y∈D x , y ∈ D 及实数 α∈[0,1] α ∈ [ 0 , 1 ] ,都有 αx+(1−α)y∈D α x + ( 1 − α ) y ∈ D
则称集合 D D 为凸集。
由凸集的定义可以看出凸集的几何意义,对于非空集合 D D ,连接 D D 中任意两点 x,y x , y 的线段仍属于该集合,则该集合 D D 是凸集。
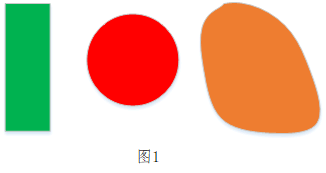
图1所示的图形是凸集,图2显示的图形是非凸集。

凸函数定义:
设函数 f(x) f ( x ) 定义在凸集 D⊂Rn D ⊂ R n 上,若对于任意的 x,y∈D x , y ∈ D 及任意实数 α∈[0,1] α ∈ [ 0 , 1 ] ,都有 f[αx+(1−α)y]≤αf(x)+(1−α)f(y) f [ α x + ( 1 − α ) y ] ≤ α f ( x ) + ( 1 − α ) f ( y ) ,则称 f(x) f ( x ) 为凸集 D D 上的凸函数。
凸函数的充分必要条件:
(一阶条件)
设在凸集 D⊂Rn D ⊂ R n 上 f(x) f ( x ) 可微,则 f(x) f ( x ) 在 D D 上为凸函数的充分必要条件是对任意的 x,y∈D x , y ∈ D 都有 f(y)≥f(x)+∇f(x)T(y−x) f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x )
证明:
必要性。 设 f(x) f ( x ) 是 D D 上的凸函数。任取 x,y∈D x , y ∈ D 及 α∈[0,1] α ∈ [ 0 , 1 ] ,有
f[αy+(1−α)x]≤αf(y)+(1−α)f(x) f [ α y + ( 1 − α ) x ] ≤ α f ( y ) + ( 1 − α ) f ( x )
即
f[x+α(y−x)]≤f(x)+α[f(y)−f(x)] f [ x + α ( y − x ) ] ≤ f ( x ) + α [ f ( y ) − f ( x ) ]
由泰勒公式有
f[x+α(y−x)]=f(x)+α∇f(x)T(y−x)+o(∥α(y−x)∥) f [ x + α ( y − x ) ] = f ( x ) + α ∇ f ( x ) T ( y − x ) + o ( ‖ α ( y − x ) ‖ )
代入上式得
f(y)−f(x)≥∇f(x)T(y−x)+o(∥α(y−x)∥)α f ( y ) − f ( x ) ≥ ∇ f ( x ) T ( y − x ) + o ( ‖ α ( y − x ) ‖ ) α
上式两端取极限,令 α→0 α → 0 有
f(y)≥f(x)+∇f(x)T(y−x) f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x )
充分性。因为 D D 为凸集,所以设任意的 x,y∈D x , y ∈ D , α∈[0,1] α ∈ [ 0 , 1 ] ,则 αx+(1−α)y∈D α x + ( 1 − α ) y ∈ D
令 αx+(1−α)y=z α x + ( 1 − α ) y = z ,有
f(x)−f(z)≥∇f(z)T(x−z)f(y)−f(z)≥∇f(z)T(y−z) f ( x ) − f ( z ) ≥ ∇ f ( z ) T ( x − z ) f ( y ) − f ( z ) ≥ ∇ f ( z ) T ( y − z )
用 α,1−α α , 1 − α 分别乘上面两式得
α[f(x)−f(z)]≥α∇f(z)T(x−z)(1−α)[f(y)−f(z)]≥(1−α)∇f(z)T(y−z) α [ f ( x ) − f ( z ) ] ≥ α ∇ f ( z ) T ( x − z ) ( 1 − α ) [ f ( y ) − f ( z ) ] ≥ ( 1 − α ) ∇ f ( z ) T ( y − z )
相加并整理得
α[f(x)−f(z)]+(1−α)[f(y)−f(z)]≥α∇f(z)T(x−z)+(1−α)∇f(z)T(y−z)αf(x)−αf(z)+f(y)−f(z)−αf(y)+αf(z)≥∇f(z)T[αx−αz+y−z−αy+αz]αf(x)+(1−α)f(y)−f(z)≥∇f(z)T[αx+(1−α)y−z]=0αf(x)+(1−α)f(y)≥f(z) α [ f ( x ) − f ( z ) ] + ( 1 − α ) [ f ( y ) − f ( z ) ] ≥ α ∇ f ( z ) T ( x − z ) + ( 1 − α ) ∇ f ( z ) T ( y − z ) α f ( x ) − α f ( z ) + f ( y ) − f ( z ) − α f ( y ) + α f ( z ) ≥ ∇ f ( z ) T [ α x − α z + y − z − α y + α z ] α f ( x ) + ( 1 − α ) f ( y ) − f ( z ) ≥ ∇ f ( z ) T [ α x + ( 1 − α ) y − z ] = 0 α f ( x ) + ( 1 − α ) f ( y ) ≥ f ( z )
即
αf(x)+(1−α)f(y)≥f[αx+(1−α)y] α f ( x ) + ( 1 − α ) f ( y ) ≥ f [ α x + ( 1 − α ) y ]
故
f(x) f ( x ) 在
D D 上是凸函数。
(二阶条件)
设在开凸集 D⊂Rn D ⊂ R n 内 f(x) f ( x ) 二阶可微,则 f(x) f ( x ) 是 D D 内的凸函数的充分必要条件为在 D D 内任意一点 x x 处, f(x) f ( x ) 的海色(Hesse)矩阵 G(x) G ( x ) 半正定,其中
G(x)=∇2f(x)=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x12∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22⋯∂2f∂x2∂xn⋮⋮⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂xn2⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥ G ( x ) = ∇ 2 f ( x ) = [ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋮ ⋮ ⋮ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ]
证明:
必要性。任取 x∈D x ∈ D 及 y∈Rn(y≠0) y ∈ R n ( y ≠ 0 ) ,因为 D D 为开集,所以存在 ε>0 ε > 0 ,当 α∈[−ε,ε] α ∈ [ − ε , ε ] 时, x+αy∈D x + α y ∈ D ,由一阶条件可得
f(x+αy)≥f(x)+α∇f(x)Ty f ( x + α y ) ≥ f ( x ) + α ∇ f ( x ) T y
由泰勒公式有
f(x+αy)=f(x)+α∇f(x)Ty+12α2yTG(x)y+o(α2) f ( x + α y ) = f ( x ) + α ∇ f ( x ) T y + 1 2 α 2 y T G ( x ) y + o ( α 2 )
由此可得
12α2yTG(x)y+o(α2)≥0 1 2 α 2 y T G ( x ) y + o ( α 2 ) ≥ 0
所以
yTG(x)y+o(α2)α2≥0 y T G ( x ) y + o ( α 2 ) α 2 ≥ 0
令 α→0 α → 0 ,取极限得
yTG(x)y≥0 y T G ( x ) y ≥ 0
即 G(x) G ( x ) 半正定。
充分性。任取 x,y∈D x , y ∈ D ,因为 G(x) G ( x ) 半正定,由泰勒公式可得
f(y)=f(x)+∇f(x)T(y−x)+12(y−x)TG(ξ)(y−x)≥f(x)+∇f(x)T(y−x) f ( y ) = f ( x ) + ∇ f ( x ) T ( y − x ) + 1 2 ( y − x ) T G ( ξ ) ( y − x ) ≥ f ( x ) + ∇ f ( x ) T ( y − x )
其中 ξ=x+α(y−x),α∈(0,1) ξ = x + α ( y − x ) , α ∈ ( 0 , 1 )
由一阶条件可得 f(x) f ( x ) 为凸函数。

