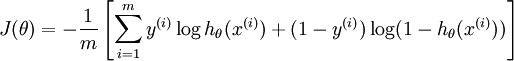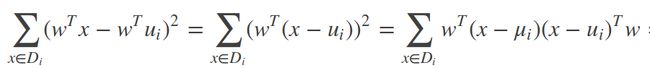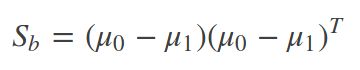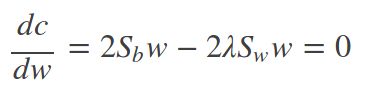分类算法（一）：广义线性模型之线性回归、逻辑回归
线性回归——正态分布来分析误差； 逻辑回归——伯努利分布来分析误差
线性回归用来做预测,LR用来做分类。线性回归是来拟合函数,LR是来预测函数。线性回归用最小二乘法来计算参数,LR用最大似然估计来计算参数。线性回归更容易受到异常值的影响,而LR对异常值有较好的稳定性。
线性回归（回归）
线性回归通常是解决连续数值预测问题, 利用数理统计的回归分析, 来确定变量之间的相互依赖关系。线性回归中的因变量是连续的。其公式通常表示如下:
均方误差损失函数（假设正态分布，又名高斯分布）：
，
均方误差通过最小二乘法（对
求导）求解得到
：
逻辑回归 （分类）
逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层逻辑函数g(z)。逻辑回归中的因变量是离散的。
逻辑回归通常用来解决二分类问题(也可以解决多分类问题), 用于估计某种事物的可能性。需要一个单调可微分的函数将输出值归一化到 (0, 1) 之间, Sigmoid 函数形式如下:
Sigmoid函数的求导公式：
函数经过变化可以得到如下，表示为真实标记的对数几率：
损失函数（假设伯努利分布）：
假设因变量y服从伯努利分布，取值为0和1，那么可以得到下列两个式子（分子分母同时乘以e）：
通过极大似然函数对模型最大化“对数似然”：![\ln L(w,b)= \sum _{i=1}^{m}\ln p(y_{i}|x;w,b)= \sum _{i=1}^{m}\ln [p_{i}^{y_{i}}\cdot (1-p_{i})^{1-y_{i}}]](http://img.e-com-net.com/image/info8/fea23b0a69ef4e18bb1fda4734ae5712.gif)
代入Sigmoid 函数，转化求解可得：
![ln L(w,b)= \sum _{i=1}^{m}[y_{i}\ln p_{i} + (1-y_{i})\ln(1-p_{i})] =- \sum _{i=1}^{m}[-y_{i}\cdot wx_{i} + \ln (1+e^{wx_{i}})]](http://img.e-com-net.com/image/info8/252ac4df687f487d95aa5fd3535ba11d.gif)
最大化最大似然，等价于最小化如下公式，即损失函数可以通过最小化负的似然函数得到：
![ln L(w,b)= \sum _{i=1}^{m}[-y_{i}\cdot w^{T}x_{i} + \ln (1+e^{w^{T}x_{i}})]](http://img.e-com-net.com/image/info8/31ad9fd4f9d24fa2bcd7694ac566e054.gif)
求解方式通过梯度下降（对ｗ求导）
，如果只用一个训练样例（x，y），采用随机梯度上升规则，那么随机梯度上升更新规则为：
对数损失函数，取整个数据集上的平均对数似然损失：
优点：
线性回归在整个实数域内敏感度一致，而分类范围，需要在[0,1]之内。而逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型。逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为(0,1)。
逻辑回归怎么实现多分类
１）所有类别之间有明显的互斥则使用softmax分类器：
修改逻辑回归的损失函数,使用softmax函数构造模型解决多分类问题,softmax分类模型会有相同于类别数的输出,输出的值为对于样本属于各个类别的概率,最后对于样本进行预测的类型为概率值最高的那个类别。
２）所有类别不互斥有交叉：
根据每个类别都建立一个二分类器,本类别的样本标签定义为0,其它分类样本标签定义为1,则有多少个类别就构造多少个逻辑回归分类器。
线性判定分析
LDA:
最大化目标：分子－类间散度矩阵
；分母－类内散度矩阵
，如下分别是类内协方差和目标函数：
其中，μi：表示第i类训练样本的均值 ，μ：是所有样本的均值向量 ，直线w
定义过类内散度矩阵和类间散度矩阵后，我们可以将上述的优化目标重新写为：
注意到上式的分子和分母都是关于w的二次项，因此上式的解与w的长度无关,只与其方向有关。不失一般性，令分母=1,则上式等价于最大化分子：
使用拉格朗日乘子法可以得到：
因为
的方向恒为
，令
，可得：
对进行奇异值分解，
可以得到
多分类学习类别不平衡问题
１．欠采样
２．过采样
３．直接基于原始训练集学习，进行阈值移动，将下式嵌入决策过程中：
LR和线性回归的区别
1.应用：线性回归用来做预测,LR用来做分类。
2.函数：线性回归是来拟合函数,LR是来预测函数。
3.参数计算：线性回归用最小二乘法来计算参数,LR用最大似然估计来计算参数。
4.鲁棒性：线性回归更容易受到异常值的影响,而LR对异常值有较好的稳定性。