通俗理解集成学习boosting和bagging和随机森林

转载自csdn各种资料

First，What is Ensemble Learning

1.将多个分类方法聚集在一起，以提高分类的准确率（可以是相同or不同算法）

2.集成学习法由训练数据构建一组基分类器，然后通过对每个基分类器的预测进行投票来进行分类

3.严格来说，集成学习并不算是一种分类器，而是一种分类器结合的方法。

4.如果把单个分类器比作一个决策者的话，集成学习的方法就相当于多个决策者共同进行一项决策。

那就产生了两个问题。

1.怎么训练每个基分类器？

2.怎么融合每个基分类器

Then，we have bagging and boosting

集成学习大致分为两类，一类串行生成，如Boosting。一类为并行化，如Bagging。

1.Bagging

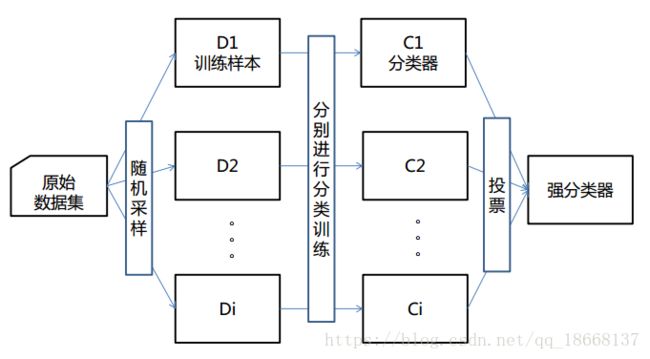
1.Bagging又叫自助聚集，是一种根据均匀概率分布从数据中重复抽样（有放回）的技术。

2. 每个抽样生成的自助样本集上，训练一个基分类器；对训练过的分类器进行投票，将测试样本指派到得票最高的类中。

3.每个自助样本集都和原数据一样大

4.有放回抽样，一些样本可能在同一训练集中出现多次，一些可能被忽略。

如下图

举个例子吧。

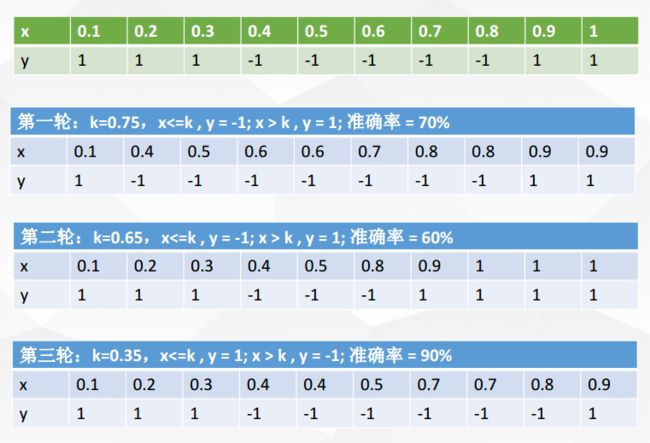
X 表示一维属性，Y 表示类标号（1或-1）测试条件：当x<=k时，y=？；当x>k时，y=？；k为最佳分裂点

下表为属性x对应的唯一正确的y类别

现在进行5轮随机抽样，结果如下

每一轮随机抽样后，都生成一个分类器

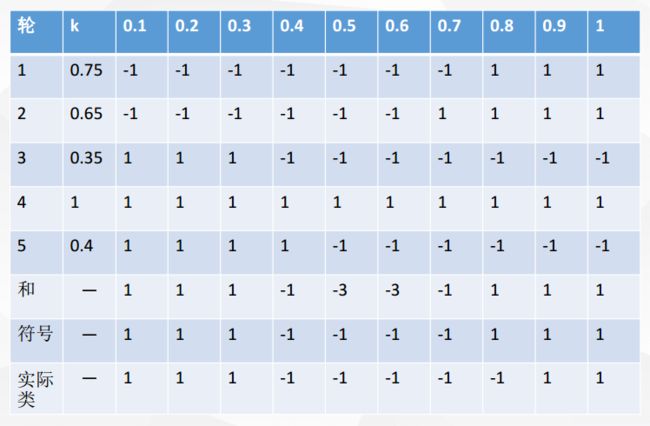
然后再将五轮分类融合

对比符号和实际类，我们可以发现：在该例子中，Bagging使得准确率可达90%

总结一下：

1.由于每个样本被选中的概率相同，因此bagging并不侧重于训练数据集中的任何特定实例

2.从偏差-方差的角度，Bagging主要关注降低方差，因此它在容易受到样本扰动的学习器（如不剪枝的决策树、神经网络）中效果更明显。意思就是说不容易受极端样本影响，因为最后是投票的，所以降低了方差

 

2.boosting

1.boosting是一个迭代的过程，用于自适应地改变训练样本的分布，使得基分类器聚焦在那些很难分的样本上

2.boosting会给每个训练样本赋予一个权值，而且可以再每轮提升过程结束时自动地调整权值。开始时，所有的样本都赋予相同的权值1/N，从而使得它们被选作训练的可能性都一样。根据训练样本的抽样分布来抽取样本，得到新的样本集。然后，由该训练集归纳一个分类器，并用它对原数据集中的所有样本进行分类。每轮提升结束时，更新训练集样本的权值。增加被错误分类的样本的权值，减小被正确分类的样本的权值，这使得分类器在随后的迭代中关注那些很难分类的样本。

算法如下：

first，训练一个基学习机，对训练样本进行学习

对于识别错的样本进行额外关注，从而对训练样本分布进行调整

then，用新样本分布训练下一个学习机

repeat.........................

last，将这若干个基学习机进行加权结合。

说好的通俗呢。。。。。。。。。。。。。。。。。。。。。。。。。。。。

例子来咯，公司开会，要解决很多问题，

第一个人先来解决，这时候，有的问题被他很好的解决了，而有的问题（如市场推广问题）并没有很好的被解决。此刻，我们会将他并不能解决的问题给予更多的关注。怎么做，就是加大权重咯，也就是让第二个人更加关注这个问题吖，而对这个人已经解决了的问题则减少它的权重。

第二个人，知道上一个人市场推广这个问题没解决好，就重点讲一下自己对这个问题的想法，

当然也会根据每个人解决问题的能力赋予每个人不一样的权重，能力越高权重越大，比如市场部的，对市场的话语权较多，或者老板，权重更大。

直到有一天，遇到一个问题我们大家都不知道答案，然后大家分别去发表自己的观点，最后的结果是综合大家的看法给出的。也就是每个人的观点会结合这个人的权重之后综合得出。这里，每个人就是一个个的弱分类器。大家一起这样的组合就是强分类器。

3.随机森林

以决策树为基学习器构建Bagging集成，进一步在决策树的训练过程中引入随机属性选择。传统决策树在选择划分属性的时候是在当前节点所有的属性集合中选出一个左右属性进行划分；而在RF中，对基决策树的每个节点，先从该节点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分。这里的参数k控制了随机性的引入程度。如果k=d（全部属性集），则基决策树的构建=传统决策树构建。如果k=1，基决策树每个节点随机选择一个属性进行划分。一般推荐k=log2d。

4.对比Bagging和Boosting

1）样本选择上：

Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的，子集的数量等于样本的数量。

Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。

2）样例权重：

Bagging：使用均匀取样，每个样例的权重相等

Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大.

3）预测函数：

Bagging：所有预测函数的权重相等.

Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重.

4）并行计算：

Bagging：各个预测函数可以并行生成

Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果.

5.对比Bagging和随机森林

1）样本选择上：

都是有放回的随机选取子集

2）个体决策树的属性：

Bagging每颗个体决策树的结点要对所有属性进行考察；

随机森林的个体决策树的结点对一部分属性进行考察；

3）泛化性能：

随着个体决策树的数量增加，Bagging和随机森林泛化性能都有所增加。

在个体决策树数量很少时，随机森林性能较差，因为只包含若干属性，但随着学习器的增加，性能很快就会变好，且强于Bagging。

结束语

从偏差-方差分解的角度来看，Boosting主要关注降低偏差，因为他更加关注分类错误的样本，而bagging更加关注降低方差，因为他不容易受极值点影响，多说一句，偏差相当于预测准确性，而方差相当于预测稳定性，下图就能明显的说明偏差和方差。