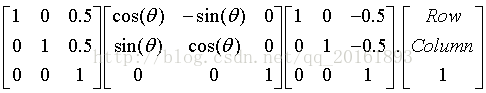Halcon学习（四）图像处理中的两个坐标系

写在前面：

从“矩阵都是对基的变换”这个角度去理解仿射变换，这样更为直观。

        矩阵的学习应从矩阵的几何意义入手

 

一   参考MATLAB文档

1.  Pixel  Indices （matlab文档）
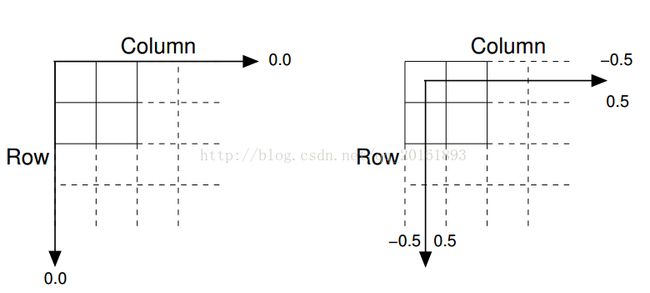
origin in upper left corner of the image  （pixel 和 image 都是这个坐标系），左上角的像素坐标为（1,1），右边的像素为（1,2），像素坐标表示为（Row，Column），元素之间是离散的，如下图所示。

2. Spatial Coordinates

（1） Intrinsic Coordinate System（matlab文档）
origin  in the middle of the upper left pixel  （area_center等是在这个坐标系下进行计算），The coordinates(x,y) of the center point of any pixel areidentical to the column and row indices for that pixel。一定要注意的是，图片左上角的坐标为（0.5,0.5）（此处有疑问，Halcon文档中图片左上角的坐标为（-0.5，-0.5），还是以Halcon中为准），而不是（0,0），图片右下角的坐标为（ColsNum+0.5,RowsNum+0.5）。 From this Cartesian（笛卡尔） perspective, an (x,y) location such as (3.2,5.3) is meaningful, and is distinct from pixel (5,3).

 

二   参考Halcon文档

The different tasks in HALCON need different image coordinate systems,the positions for pixel-precise regions differ from those used for subpixel-precise XLD contours by 0.5 pixels,the estimated position returned by the matching can not be used directly but is optimized for the creation of the transformation matrices that are used to apply the applications described above.

The difference between affine_trans_pixel and affine_trans_point_2d lies in the used coordinate system: affine_trans_pixel uses a coordinate system with origin in the upper left corner of the image, The coordinate system runs from (0,0) (upper left corner) to (Width-1,Height-1).  while affine_trans_point_2d uses the standard image coordinate system, whose origin lies in the middle of the upper left pixel and which is also used by operators like area_center.
In contrast to affine_trans_point_2d,affine_trans_pixel first converts the input coordinates from HALCON's standard coordinate system(with the origin in the center of the upper left pixel) to a coordinate system with the origin in the upper left corner of the upper left pixel. After the transformation with HomMat2D  the result is converted back to the standard coordinate system.

 

*测试程序1：
gen_rectangle1(Rect,0,0,0,0)area_center(Rect,Area, Row, Column) 以上代码绘制一个像素大小的矩形，Row=0，Column=0
*测试程序2：
gen_rectangle1 (Rect, 0, 0, 1,1)area_center(Rect,Area, Row, Column)绘制四个像素大小的矩形，Row=0.5，Column=0.5
HALCON中的两个图像坐标示意图如下所示：

                                                                                  

          

affine_trans_point_2d use the right coordinate system,the standard image coordinate system for which a position corresponds to the center of a pixel 
.In contrast ,the operators  affine_trans_pixel, affine_trans_contour_xld,affine_trans_region, andaffine_trans_image use the coordinate system depicted in
figure left. 

halcon算子affine_trans_image reference 中有如下说明：
 for example, if you use this operator to calculate the center of gravity of a rotationally symmetric image and then rotate the image around this
 point using hom_mat2d_rotate, the resulting image will not lie on the original one.In such a case（特指绕中心点旋转的情况），you can compensate       this effect
by applying the following translations to HomMat2D before using it in affine_trans_image:

  area_center(Image,Area,Row,Column)
  vector_angle_to_rigid(Row,Column,0,Row,Column,rad(90),HomMat2D)
  hom_mat2d_translate(HomMat2D, 0.5, 0.5, HomMat2DTmp)
  hom_mat2d_translate_local(HomMat2DTmp, -0.5, -0.5, HomMat2DAdapted)
  affine_trans_image(Image, ImageAffinTrans, HomMat2DAdapted, 'constant', 'false')  

**
如果将Row和Column的求法换为如下方法，就不需要translate和translate-local这两步get_image_size(Image,Width,Height)
Row := Height/2 
Column := Width/2

 

这个地方之所以要对旋转矩阵进行变换，是因为旋转中心点的坐标是基于标准图像坐标系,图片左上角的坐标是（0.5,0.5）。
hom_mat2d_translate 是矩阵左乘
hom_mat2d_translate_local 是矩阵右乘，基于本地坐标系
Row和Column指的的是图片像素坐标

  经过以上矩阵变换后再对图片旋转90度，如右图所示，可以发现旋转前后的图片位于同一位置（此时旋转发生在标准图像坐标系，而非像素坐标系）。左图中未对旋转进行进行调整，显然可知旋转前后的图片并不在同一位置。
需要注意的是，假如程序修改为
hom_mat2d_translate(HomMat2D,-0.5,-0.5,HomMat2DTmp)
hom_mat2d_translate_local(HomMat2DTmp,0.5,0.5,HomMat2DAdapted)
旋转后图片位置也会偏移。

                                                                           

如下操作，旋转后的图片也是重合的。（旋转发生在像素坐标系下，而非标准图像坐标系）

area_center(Circle,Area, Row,Column)
vector_angle_to_rigid(Row+0.5,Column+0.5,0,Row+0.5,Column+0.5,rad(90),HomMat2D)
affine_trans_image(ImageResult,ImageAffinTrans2,HomMat2D,'constant', 'false')



 

 

相关资料：

 

（1）origin pixel in the image coordinate system in opencv

（2）Question about coordinate system in matlab

（3）Image Coordinate SystemsMATLAB文档中也讲到了 Image Coordinate System 

（4）affine transformation matrix 仿射变换矩阵 与 OpenGL

 

 

（5）http://www.itwendao.com/article/detail/139651.html

 

 

参考资料（5）中有如下描述：

affine_trans_pixel 和 affine_trans_point_2d的不同在于所使用的坐标系原点不同，affine_trans_pixel 使用的是像素坐标系， 即原点位于图像的左上角第一个像素，使用row和column来确定像素位置，而affine_trans_point_2d的原点位于左上角第一个像素的中心，使用x和 y来标识坐标位置（实际原点相差（0.5，0.5））。并且在使用affine_trans_point_2d时如果使用标准图像坐标系，则row坐标必须传递Px，列坐标必须传递Py以保证旋转方向的正确性。（这句话如何理解？既然如此，那为什么还用Px，Py，而不是Row ，Column）
HALCON文档中 Description：

1)  affine_trans_point_2d（：：HomMat2D,Px,Py：Qx,Qy）
If the points to transform are specified in standard image coordinate,their row coordinate must be passed  in Px and their column coordinate in Py. This is necessary to obtain a right-handed coordinate system for the image. In particular,this assure that rotations are performed in the correct direction. Note that the (x,y) order of the matircs quite naturally correspond to the usual (Row,Column) order for coordinate in the image.

2) hom_mat2d_translate（：：HomMat2D,Tx,Ty：HomMat2DTranslate）
It should be noted that homogeneous transformation matircs refer to a general right-handed mathematical coordinate system. If a homogeneous transformation matrix is used to transform images,regions,XLD contours,or any other data that has been extracted from images,the row coordinates of the transformation must be passed in the x coordinates,whilethe column must be passed in the y coordinates. Consequently,the order of passing row and column coordinates follows the usual order(Row,Column).This convention is essential to obtain aright-handed coordinate system for the transformation of iconic data,and consequently to ensure in particular that rotations are performed in the correct mathematical direction.