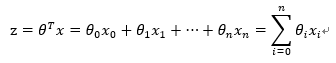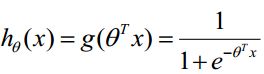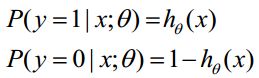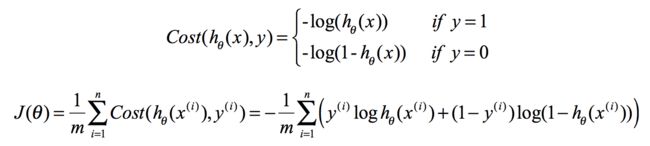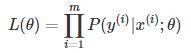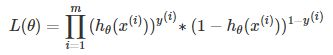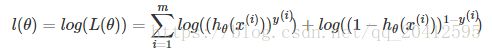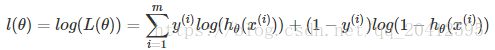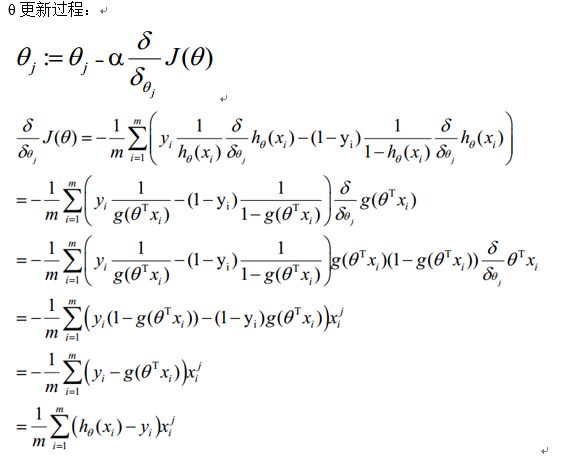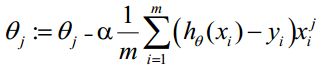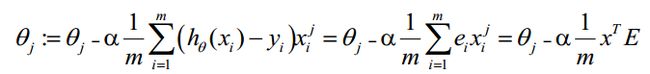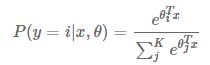机器学习算法（1）之逻辑回归算法

Logistic Regression（逻辑回归）是机器学习中一个非常常见且非常重要的模型，在实际中也常常被使用，是一种经典的分类模型（不是回归模型）。本文主要介绍了Logistic Regression（逻辑回归）模型的原理以及参数估计、公式推导。

---

一、逻辑回归基本概念

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）。

Logistic回归的主要用途：

• 寻找危险因素：寻找某一疾病的危险因素等；
• 预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；
• 判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。

这里也记录一下逻辑回归的应用。

一个是在美团上的应用，主要作用是： 

1、预测一个用户是否点击特定的商品 
2、判断用户的性别 
3、预测用户是否会购买给定的品类 
4、判断一条评论是正面的还是负面的

第二个应用是腾讯APP的推荐，据说也是使用逻辑回归预测应用宝里用户是否会下载某个APP。

常规步骤

Regression问题的常规步骤为：

1. 寻找h函数（即hypothesis）；
2. 构造J函数（损失函数）；
3. 想办法使得J函数最小并求得回归参数（θ）

 

二、模型

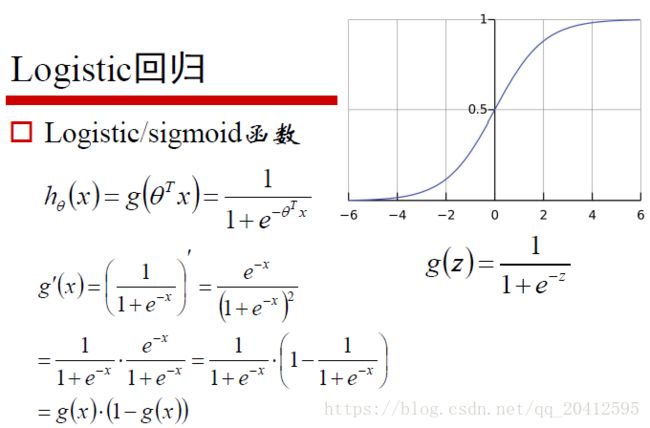
1）sigmoid 函数

在介绍逻辑回归模型之前，我们先引入sigmoid函数，其数学形式是：

从上图可以看到sigmoid函数是一个s形的曲线，它的取值在[0, 1]之间，在远离0的地方函数的值会很快接近0/1。这个性质使我们能够以概率的方式来解释（后边延伸部分会简单讨论为什么用该函数做概率建模是合理的)。

我们知道，线性回归的公式如下： 

而对于Logistic Regression来说，其思想也是基于线性回归（Logistic Regression属于广义线性回归模型）。其公式如下： 

2）构造预测函数为：

函数h(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

3）构造损失函数J（m个样本，每个样本具有n个特征）

Cost函数和J函数如下，它们是基于最大似然估计推导得到的。

4）损失函数详细推导过程

根据上式，接下来我们可以使用概率论中极大似然估计的方法去求解损失函数，首先得到概率函数为： 

因为样本数据(m个)独立，所以它们的联合分布可以表示为各边际分布的乘积,取似然函数为： 

取对数似然函数： 

最大似然估计就是求使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。

最大似然估计就是要求得使 l(θ)取最大值时的 θ，这里我们稍微变换一下： 

因为乘了一个负的系数−1m−1m，然后就可以使用梯度下降算法进行参数求解了。

5）梯度下降法求解最小值

θ更新过程可以写成：

6）向量化Vectorization

Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。

如上式，Σ(...)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。 
θ更新过程可以改为：

综上所述，Vectorization后θ更新的步骤如下：

1. 求 A=x*θ
2. 求 E=g(A)-y
3. 接下来，便求

 

三、 正则化

正则化方法 （减轻过拟合的问题，见前面的文章，有讲过拟合的原因及对策）
       正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化项就越大。

一般情况下，取p=1或p=2，分别对应L1，L2正则化，两者的区别可以从下图中看出来，L1正则化（左图）倾向于使参数变为0，因此能产生稀疏解。

实际应用时，由于我们数据的维度可能非常高，L1正则化因为能产生稀疏解，使用的更为广泛一些。

是正则项系数： 
• 如果它的值很大，说明对模型的复杂度惩罚大，对拟合数据的损失惩罚小，这样它就不会过分拟合数据，在训练数据上的偏差较大，在未知数据上的方差较小，但是可能出现欠拟合的现象； 
• 如果它的值很小，说明比较注重对训练数据的拟合，在训练数据上的偏差会小，但是可能会导致过拟合。 
 

四、延伸--多元逻辑回归

多分类（softmax)

       如果y不是在[0,1]中取值，而是在K个类别中取值，这时问题就变为一个多分类问题。有两种方式可以出处理该类问题：一种是我们对每个类别训练一个二元分类器（One-vs-all），当K个类别不是互斥的时候，比如用户会购买哪种品类，这种方法是合适的。如果K个类别是互斥的，即 y=i的时候意味着 y不能取其他的值，比如用户的年龄段，这种情况下 Softmax 回归更合适一些。Softmax 回归是直接对逻辑回归在多分类的推广，相应的模型也可以叫做多元逻辑回归（Multinomial Logistic Regression）。

模型通过 softmax 函数来对概率建模，具体形式如下：

而决策函数为：

五、LogisticRegression中模型参数

来自官网

class sklearn.linear_model.LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True, 

intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', 

verbose=0, warm_start=False, n_jobs=1)

一些重要的参数：

penalty : str, ‘l1’ or ‘l2’, default: ‘l2’，惩罚项，分别是L1与L2正则化；

C : float, default: 1.0，特别注意，这里C是正则化项的系数，而且是正则化强度的 倒数，越小意味着更强的正则化。

Inverse of regularization strength; must be a positive float. Like in support vector machines, smaller values specify stronger regularization.（正则化强度的倒数；必须是正浮点。像支持向量机一样，较小的值指定更强的正则化。）

fit_intercept : bool, default: True 是否拟合截距

class_weight : dict or ‘balanced’, default: None 是否要对样本加权

multi_class : str, {‘ovr’, ‘multinomial’}, default: ‘ovr’  多分类的处理方法

 

六、逻辑回归总结

优点：

• 算法简单，训练速度快，在超大数据量情况下有很大的优势
• 模型的可解释性好（比如能直接输出系数和截距）
• 是深度神经网络算法的基础

不足：

• 模型的预测精度一般，容易欠拟合

经典应用场景：互联网领域最常用的算法

• CTR预估，推荐排序
• 信用评分（比如蚂蚁花瓣）
• 大规模在线学习

 

参考资料：

https://blog.csdn.net/pakko/article/details/37878837

https://blog.csdn.net/chibangyuxun/article/details/53148005

https://blog.csdn.net/programmer_wei/article/details/52072939

https://tech.meituan.com/intro_to_logistic_regression.html

https://blog.csdn.net/wjj5881005/article/details/52510521