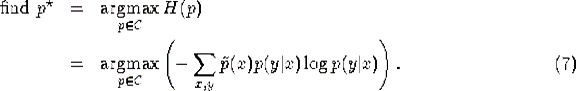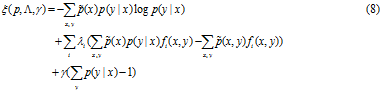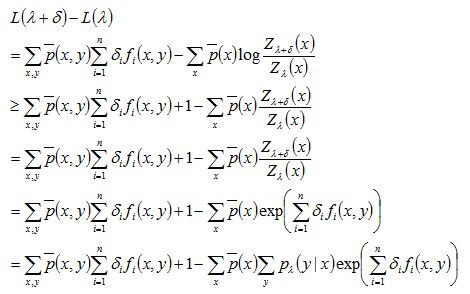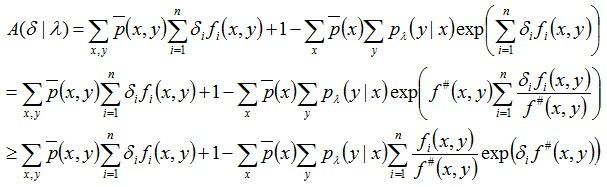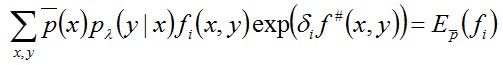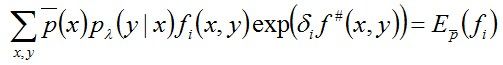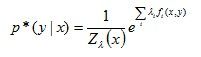逻辑斯蒂回归模型与最大熵模型
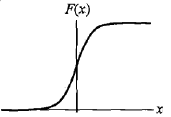
分布函数：
F(X)= p( X <= x ) = 1 / (1 + exp(-(x-u)/γ))
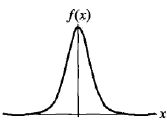
密度函数：
f(x)= F`(x) = exp(-(x-u)/γ) / γ(1 + exp(-(x-u)/γ))2
式中：u为位置参数，γ >0为形状参数（γ越小，曲线在中心增长越快）
二项逻辑斯蒂回归模型
P(Y=1 l x)=exp(w*x+b) / [1+exp(w*x+b)]
P(Y=0 l x)= 1 / [1+exp(w*x+b)]
有时为了方便，将b并入w向量中
最后写成：
P(Y=1 l x)=exp(w.*x) / [1+exp(w*x)]
P(Y=0 l x)= 1 / [1+exp(w.*x)]
给定实例，可以分别求得P（Y=1）和P（Y=0）的值，将实例分配到概率较大的一方
事件发生几率（odds）
如果事件发生概率为p，那么该事件的几率是 p / (1-p)
对数几率或logit函数：
logit(p)=log [p /(1-p) ]
对于逻辑斯蒂回归而言
log [ P(Y-1) / [1-P(y=1)] ]=w.*x
模型参数估计
即令L'(w)=0
我们的约束优化问题是：
我们将这个称为原始问题（primal）。简单的讲，我们目标是在满足以下约束的情况下，最大化H(p)。
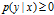
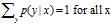显然概率和为1
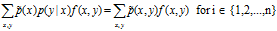假设训练数据与模型的P（X）的期望相同，f（x）是特征函数
为了解决这个优化问题，引入Lagrangian 乘子。
实值参数
和
对应施加在解上的n+1个约束。
IIS的推导过程
IIS是一种最大熵学习模型的最优化算法，其推导过程如下：
目标是通过极大似然估计学习模型参数求对数似然函数的极大值 
。
IIS的想法是：假设最大熵模型当前的参数向量是λ = (λ1, λ2, …, λn)T，我们希望找到一个新的参数向量λ + δ= (λ1+δ1, λ2+δ2, …, λn+δn)T，使得模型的对数似然函数值增大。如果能有这样一种参数向量更新的方法F：λ ->λ+δ，那么就可以重复使用这一方法，直至找到对数似然函数的最大值。
对于给定的经验分布
，模型参数从λ到λ+δ，对数似然函数的该变量是
PS：上面 >= 的推导是根据不定时：-loga >= 1 - a， a > 0
将上述求得的结果(最后一行)记为A(δ| λ)，于是有：
L( λ+ δ ) – L( λ ) >= A(δ | λ)
为了进一步降低这个下界，即缩小A(δ | λ)，引入一个变量：
因为fi是二值函数，故f#(x,y)表示的是所有特征(x, y)出现的次数，然后利用Jason不等式，可得：
我们把上述式子求得的A(δ | λ)的下界记为B(δ | λ)，即：
相当于B(δ | λ)是对数似然函数增加量的一个新的下界，可记作：L(λ+δ)-L(λ) >= B(δ | λ)。
接下来，对B(δ| λ)求偏导，得：
此时得到的偏导结果只含δ，除δ之外不再含其它变量，令其为0，可得：
从而求得δ，问题得解。
IIS算法描述
输入：
特征函数f1, f2, …,fn；经验分布
，模型Pλ(y|x)
输出：
最优参数值λi*；最优模型Pλ。
解：
1，对所有i∈{1, 2, …, n}，取初值λi = 0
2，对每一i∈{1, 2, …, n}：
a)令δi是如下方程(这里将其称作方程一)
的解，这里：
b)更新λi的值：λi <- λi + δi
3，如果不是所有λi都收敛，则重复步骤2。
这一算法的关键步骤是a)，即求解a)中方程的δi。
如果f#(x, y) 是常数，即对任何x, y，有f#(x,y) = M，那么δi可以显示的表示成：
如果f#(x, y) 不是常数，那么必须通过数值计算求δi，而简单有效的方法是牛顿法。以g(δi) = 0，表示上面的方程一，牛顿法通过迭代求的δi，使得g(δi*)= 0。迭代公式是：
求得了δ，便相当于求得权值λ，最终将λ 回代到下式中：
即得到最大熵模型的最优估计。
摘自：http://blog.csdn.net/xueyingxue001/article/details/50773917