概率图学习——Particle-Based Approximate Inference

Inference的定义：给定部分观察值E=e，求目标变量Y的概率$P(Y|E=e)$或者 $\underset{y}{\mathrm{argmax}}P(Y=y|E=e)$ (最大后验概率MAP)
Particle-Based Approximate Inference （PBAI）最基本的想法是从目标分布中采样x[1], …, x[m]，然后用采样数据去估计函数$E_p(f)\approx \frac{1}{M}{\sum }_{m=1}^{M}f(x[m])$
PBAI的关键是如何从后验分布$P(x|E=e)$中采样

前向采样 Forward Sampling （FS）

从分布P(X)中利用Bayesian Network产生随机样本，使用$$P(X=e)\approx \frac{1}{M}\sum _{m=1}^{M}I(x[m]=e)$$
估计概率， 其中I(·)是指示函数
采样过程：

1. 确定X₁, … , X_n的拓扑排序
2. 按照拓扑顺序，对每个X_i进行采样，采样概率$P(X_i|p{a}_i)$，pa_i的值都已经赋过值了
3. 估计概率$P(X=e)\approx \frac{1}{M}{\sum }_{m=1}^{M}I(x[m]=e)$

从而可以估计任何期望$E_p(f)\approx \frac{1}{M}{\sum }_{m=1}^{M}f(x[m])$
如果只需要估计变量X的子集Y，使用$P(y)\approx \frac{1}{M}{\sum }_{m=1}^{M}I\{x[m](Y=y)\}$
采样开销

• 每个变量X_i的开销：O(log(Val|X_i))， 其中Val|X_i是指变量X_i的取值范围
• 每个sample的开销：$O(nlog(\underset{i}{\max }Val|X_i))$
• M个sample的开销：$O(Mnlog(\underset{i}{\max }Val|X_i))$

需要sample的数量

为了以概率$1-\delta$, 达到相对误差$<ϵ$，至少需要采样$$M\ge 3\frac{ln(2/\delta )}{P(y){ϵ}^2}$$
如果P(y) ↓，则M↑，才能更精确地观测。

Forward Sampling with Rejection

因为是要在观测到一部分变量值e得情况下求目标变量Y的概率$P(Y|E=e)$。用带拒绝的方式做采样，用前向采样采出的数据，如果E≠e，就把这个样本扔掉。从被接受的样本中去估计。
缺点/问题 如果p(e)=0.001,概率非常小，那么扔掉的样本会非常多，浪费很多样本资源。

似然采样 Likelihood Weighting （LW）

通过FS with rejection的问题，是否可以让所有的样本都满足E=e。
那么可以把在sample到观测变量X∈E时，直接设置为X=e。原来我们是从后验P(X|e)做sample，现在我们是直接从先验P(X)得到采样。
所以想从P’(X, e)中得到sample再归一化。
总结来说就是从先验分布P(X)得到样本，再用likelihood加权样本。
P(Y, e) = P(Y|e)P(e), 所以P(Y|e)是P(Y, e)的一部分
根据BN分解定理，$P(X)={\prod }_{i}P(X_i|Pa(X_i))$
观察值给了定值$E_j=e_j$, 所以每个采样值应该加上权值${\prod }_{j}P(E_j=e_j|Pa(E_j))$
和FS with rejection联系：采样可以看成有${\prod }_{j}P(E_j=e_j|Pa(E_j))$的概率被接受
采样过程

1. 确定X₁, … , X_n的拓扑排序
2. 对于每个变量X_i(采M个样本)
   如果X_i∉E，直接从$P(X_i|P{a}_i)$采样
   如果X_i∈E，设X_i=E[x_i]，$w_i=w_i\cdot P(E[x_i]|P{a}_i)$
3. 得到w_i，x[1], …, x[M]
4. 估计概率$$P(y|e)\approx \frac{{\sum }_{m=1}^{M}w[m]I\{x[m](Y=y)\}}{{\sum }_{m=1}^{M}w[m]}$$
   其中$w[m]={\prod }_{x_i\in E}P(x_i=e_i|P{a}_i)$

重要性采样 Importance Sampling （IS）

估计一个和P相关的函数Q，从Q中采样。P是目标分布，Q是采样分布。
要求Q：P(x) > 0 → Q(x) > 0
Q不会漏掉P的任何一个非零概率的事件。
在实际中，如果Q和P越想似，采样的效果自然是更好。当Q=P时，得到最低的方差估计
最简单的Q是把P的BN上的边都去掉了，即每个变量都是完全独立的。

Unnormalized Importance Sampling

左半边是从Q做sampling，右半边是对P做sampling
所以从Q中Sample的数据可以用来近似P的采样

Normalized Importance Sampling

归一化P’，P=P’/α，$\alpha ={\sum }_x{P}^{\prime }(x)$
已知α：

因此可以推导出归一化的P和Q的采样估计

所以从Q中Sample的数据可以用来近似P的采样

和刚才未归一化的做对比

Importance Sampling for Bayesian Networks

定义mutilated network（残支网络）G_E=e：

• 节点X∈E没有parents
• 在节点X∈E的CPD中只有X=E[X]那一项概率为1，其余为0
• 其余节点不变

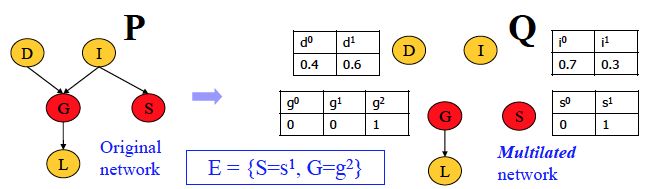
如果Q定义为mutilated network, 那么LW和IS是相同的采样公式
Likelihood Weighting:
$$P(y|e)\approx \frac{{\sum }_{m=1}^{M}w[m]I\{x[m](Y=y)\}}{{\sum }_{m=1}^{M}w[m]}$$
其中$w[m]={\prod }_{x_i\in E}P(x_i=e_i|P{a}_i)$
Importance Sampling
$$P(y|e)\approx \frac{{\sum }_{m=1}^M{P}^{\prime }(x[m])/Q(x[m])I\{x[m](Y=y)\}}{{\sum }_{m=1}^M{P}^{\prime }(x[m])/Q(x[m])}$$
其中
需要sample的数量
取决于P和Q的相似度
总结——LW和IS的不足
LW在Markov Network（MN）很低效，因为需要将MN转化为BN
IS在选择一个合适的Q上很难，如果Q和P太不像，收敛会很慢

蒙特卡洛方法 Markov Chain Monte Carlo Method（MCMC）

MCMC的基本想法是设计一个马氏链，其稳态分布是P(X|e)，即我们要求的目标分布。所以从这个马氏链上的采样就会服从我们的目标分布。
通过马氏链的稳态分布来做inference。

Markov Chain & Stationary Distribution

一个Markov Chain是regular需要满足链上所有的状态都是在有限k步内可达。
定理：一个有限状态的马氏链T有一个唯一的稳态分布 当且仅当 T是regular的。

Gibbs Sampling

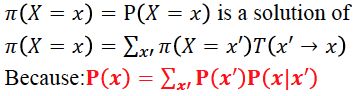
怎么判断Gibbs-sampling MC是regular的呢？

• BN：所有的CPD严格为正
• MN：所有的clique potential严格为正

采样过程（一个样本）

1. 设x[m]=x[m-1]且更换变量更新顺序(增加随机性)
2. 对每个变量X_i∈X-E：
   • 设u_i为Xi的Markov Blanket
   • 从P(X_i|u_i)采样X_i的新值
   • 更新X_i为采样值
3. 得到x[m]

Gibbs Sampling for BNs

采样过程

Gibbs Sampling for MNs

采样过程

Metropolis-Hastings Algorithm

Gibbs Sampling 给定一个当前状态 S，转移到下一个状态的转移概率是确定的，整个状态转移概率矩阵其实是确定的。
现在 MH algorithm 追求的是可以从任意一个转移分布中采到下一个样本。和 Importance sampling 有点像，可以从任意的函数 Q 中去拟合 P。
所以设计了一个新的因子：acceptance probability 接受概率。是指是否接受一个状态转移 A(x→x’)
现在的转移变成：
状态 x 转移到状态 x’：T(x→x’) = T^Q(x→x’)A(x→x’)
状态 x 停留在原状态：T(x→x) = T^Q(x→x) + ${\sum }_{x^{\prime }̸=x}$T^Q(x→x’)(1-A(x→x’))
上式第一项是原来的转移就是停留在原状态，第二项是指本来要转到其他状态，但是被拒绝了，只能留在原状态。
因为 MC 是稳态的，所以互相转移的概率是相等的。
$\pi (x)T^Q(x\to x^{\prime })A(x\to x^{\prime })=\pi (x^{\prime })T^Q(x^{\prime }\to x)A(x^{\prime }\to x)$
从上式推出：重要！！！在结构学习的时候会使用到这个结论$$A(x^{\prime }\to x)=min[1,\frac{\pi (x^{\prime })T^Q(x^{\prime }\to x)}{\pi (x)T^Q(x\to x^{\prime })}]$$
在连续概率分布结论也是成立的。经常用到的是把转移概率分布设为多元高斯分布（可以看成是以当前状态为中心的随机游走）。那么此时的转移概率是对称的（随机游走过程），即T(x’→x)=T(x→x’)。
此时的 acceptance rate 只与稳态分布或者目标分布有关，即$A(x^{\prime }\to x)=min[1,\frac{\pi (x^{\prime })}{\pi (x)}]=min[1,\frac{p(x^{\prime })}{p(x)}]$
MH algorithm 有个缺陷就是不同状态之间的转移太低效了，可能会产生很多 rejection。

(Hybrid) Hamiltonian Monte Carlo (HMC)