Markov Chain Monte Carlo
转载至https://zhuanlan.zhihu.com/p/25610149
[数据分析] Markov Chain Monte Carlo
在基础概率课我们有学过,已知一个概率分布函数F(X),那么用电脑产生服从Uniform分布的随机数U,代入,那么就是服从F(X)的随机变量。这个方法在金融领域使用很广,即Monte Carlo Simulation:通过模拟股票价格来计算期权价格。当然,这个方法很重要的一个假设是,已知概率分布函数。但很多情况下我们并没有方法得到概率分布和其反函数,因此需要其他手段。
本文翻译学习自 CHRISTOPHE ANDRIEU等人所写的An Introduction to MCMC for Machine Learning。
文章主要介绍了MCMC的重要理念,实现MCMC的流行算法,以及前沿研究。
动因
MCMC通常用于解决高维度的积分和最优化问题,这两种问题也是机器学习、物理、统计、计量等领域的基础。比如:
- 贝叶斯推论和学习,给定未知变量x和y,贝叶斯统计主要需计算以下积分:
- 标准化(normalization),即贝叶斯估计的分母
- 边缘分布(marginalisation),给定联合后验分布f(x,z),计算
- 期望(Expectation),,方差也是期望的一种
- 统计力学,用概率理论来总结一个力学系统的平均行为。。。在计算中有运用类似统计推论里计算标准化常数的方法。
- 最优化,最小化或最大化目标函数
- 带有惩罚函数的似然模型选择(Penalized likelihood model selection),分为两个步骤,一,对每一个模型计算极大似然估计参数。然后用惩罚项(如AIC,BIC)来选择复杂度和拟合度都较好的模型。
Monte Carlo原理
依据给定的目标概率分布(高维度的),产生独立同分布的样本,利用产生的样本可以对该分布进行离散式近似,其中是xi的狄拉克δ函數。然后就可以用这个近似的分布函数计算各种积分。但是,很多分布是难以直接取样的,需要借助一些方法,就是用可以直接抽样的较为简单的分布作为依据(proposal distribution)。如rejection sampling, importance sampling 和 MCMC.
狄拉克δ函數 delta-Dirac,它在除x以外的点上都等于零,且其在整个定义域上的 积分 等于1。是一种连续函数的表达式,若用离散函数来表达的话,就是
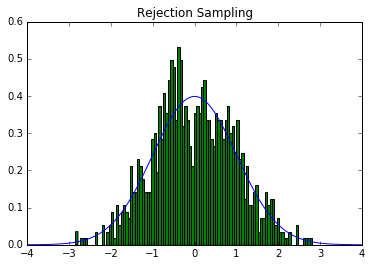
接受-拒绝抽样 (Rejection sampling)
也叫Accept-Reject Method,如一个未知分布p(x),不过能够知道他的上限。那么选取一个很好抽样的分布函数q(x)满足。然后,执行如下算法:
for i = 1 to N:
产生一个服从均匀分布的随机量u,和服从q(x)的随机量x
if u可以证明,如此这般,accepted x服从p(x)。
因为
所以
但是这个算法的限制在于:不一定经常能有这样的关系存在,以及如果M太大的话,抽样的速度会很慢,因为
用python对p(x)为标准正态分布作了个实验(code在文末)
重要性抽样 (Importance Sampling)
目标分布p(x),参考分布q(x),且p(x)=w(x)q(x),w(x)称为重要性权重。比如要计算,可以通过产生N个独立且服从q(x)的随机量,再根据w(x),就可以得到I(f)的估计。(这里不需要乘以q(x)!,因为是sample的汇总,已经把概率分布融在里面了)。离散式近似。选取q(x)令f(x)w(x)的方差最小,即最小化,可以得到最优参考分布,说明选取q(x)的时候若多考虑值很大的部分(重要区域important region)就可以得到很高的效率。这意味着,根据重要区域选取q(x)来抽样得到的结果甚至比直接使用p(x)还好!
咋看之下很奇怪,但是其实是用于应对极端情况问题的抽样,因此很适合用在金融领域。比如我们已知某风险因子(risk factor)服从p(X),然后根据风险因子计算的风险值f(X)只在X很大的时候才有值,其他时候均为0,即 ,且 很小。那么,如果单纯使用p(X)来抽样可能每抽样上千次才有一个使得f(x)>0。但是用q(x)=c|f(x)|p(x),就可以只关注重要的部分。
就是关注的问题不一样,一般是希望找到p(x)的估计,但这里我们关注的是基于p(x)的积分的估计。
下面是两个拓展:
- 随着问题的维数增大,参考分布也很难找,所以需要采用参数化参考分布,并在实际模拟中调整参数。如此就引出一种称为Adaptive importance sampling的方法。一种很潮的方法是对前述方差对求导。然后用Newton method更新,。
- 若p(x)的标准化常数无法计算,还是可以计算I(f)。,然后w(x)这时候就是真实权重的常数倍。I(f)的Monte Carlo估计,就是标准化后的重要性权重。
标准化常数(Normalizing constant):就是使概率函数变为概率密度函数的常数,比如 ,那么令 , 。
- 如果,不仅是想算积分,还想得到服从p(x)的样本,那就需要再抽样。因为前面我们只需要权重w(x)来计算积分,而得到的样本还是服从参考分布的。为了得到真正服从目标分布的样本,需要借助一个技术称为Sampling Importance Resampling(SIR)。比如想要获得M个样本,就需要重复M次对抽样,产生M个服从的样本,然后预测的目标分布就是。
根据前述 ,其实就是N个sample xi每一个被选中的概率约为w(xi),然后依此来抽样。用p(x)等于标准正态,q(x)等于均匀分布,在python中实验结果如下(code在文末)。不过即使有上述几个拓展,有的时候还是很难得到目标分布的良好估计。因此,我们需要更加英霸的技术,基于马尔科夫链。
马尔科夫链蒙地卡罗(MCMC)
是我觉得目前来看缩写最好记的方法,值得一学。
简而言之,就是用马尔科夫链方法来抽样。本文一贯的假设是目标分布p(x)难以直接抽样,但是我们对他的常数倍了如指掌(原文是“can evaluate p(x) up to a normalising constant”)
马尔科夫链
首先,xi是离散的随机序列(stochastic process),而且在每个时刻只有s个可能的值(state)。那么,这个随机序列若满足以下条件就可以称为马尔科夫链:。即每一时刻的条件概率分布只由上一期和一个转换函数/矩阵决定。
在随机微积分里对马尔科夫序列的定义是:对于任意时刻i,和任意函数f,都存在函数g,使得 ,也即未来的序列的期望值完全由现在的实现值的某种函数决定,与过去的实现值无关。
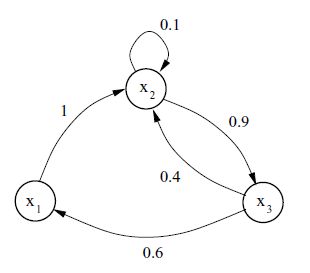
令T表示转换概率矩阵,即第i行第j列表示x的值在当期等于i的条件下在下一期转换到j的概率。若在1时刻,x的概率分布为,那么在2时刻,x的概率分布就是。马尔科夫链神奇的地方就是,只要T满足一定的条件,那么会收敛,而且不论一开始的x的概率分布是咋样,最后收敛的值都一样,为x的非条件概率分布(unconditional distribution)。
比如说下图的关系就可以用,来表示
T需要满足的条件是:
- 不可化简,即对于x任何可能的取值,都有机会(概率大于0)到达其他的取值(不一定要下一期,只要是在有限的时刻内),即上面的图是闭环的。
- 不能有死循环
另外,还有一个p(x)是可收敛分布的充分条件(非必要)是
用互联网来具象化上述两个条件的重要意义:第一个条件说明我们从任意一个网页出发都可以访问其他任何网页,而且在任何一个网页都必须可以到其他网页,而不是死循环。例如谷歌的PageRank算法就是定义T=L+E,其中L矩阵的各元素表示从一个网页到另一个网页的链接数,E是一个均匀随机数矩阵,用于满足不可化简性和排除死循环(再次的网站也要有正的概率可以摆在搜索排行前面,虽然概率很低)。
MCMC的目的就是用Markov Chain收敛于p(x)这一性质来抽样,即不管一开始抽取的样本服从什么分布,只要用了恰当的转换矩阵,经过多次转换后之后抽取的眼本就会服从目标分布。概念说起来很简单,但是转换矩阵的不同选择就形成了不同的算法。
在X是连续变量的情况下,转换矩阵T变为核函数积分形式:,
Metropolis Hasting Algorithm
最出名的算法叫做Metropolis Hasting Algorithm (MH):很多其他实用的MCMC算法究其根本都是MH算法的延伸。
算法介绍:对于目标分布p(x),首先给定参考条件概率分布q(x*|x),然后基于当前x的值模拟出一个新样本x*,然后马尔科夫链将依据一定的概率移动到x*(否则还留在x),这个概率是。具体算法伪代码如下:
1. 随便整一个x0,比如都为0
2. for i = 0 to N-1:
产生一个服从均匀分布的变量u
产生一个服从q(x*|x)的变量x*
如果u对伪代码的解释就是,如果 (粗看就是需要p(x*)>p(x)),那么链一定会移动到x*,但如果<1,那么有一定的概率会移动到x*,意思就是,如果下一个建议的值计算得出的概率密度函数值更大,那么这个值被保留在样本里的可能性更高。基本就是直方图的构建过程。
个人在 stackexchange 上看到一个很形象的比喻:假设你目前在一片高低不平的山地上,你此行的目的是在海拔越高的地方停留越久(p(x)大的时候,样本里x就多)。你的方法是随便指一个新的地方,如果这个地方的海拔更高,那么就移动过去;但如果这个地方的海拔比当前低,你就抛一个不均匀的硬币决定是否过去,而硬币的不均匀程度相当于新海拔和当前海拔的比例。也即新海拔若是当前海拔的一半,你就只有1/2的概率会过去。MH算法中q(x*|x)就是按照一定的规律指出一个新方向,A(x,x*)就是计算相对高度。
用python实现结果如下:
MH算法很简单,但是对q(x*|x)的选择非常关键。而且其他不同的算法也主要是对q的不同选择。
MH算法的转换核(transition kernel)是,其中。这个转换核满足平衡条件。
转换核就是前面的T在连续情况下可以证明,通过MH算法得到的样本就是近似服从目标分布p(x)的样本:
证明:
首先,一个转换核只要满足不可简化性和无死循环,那么这个链就一定会收敛于一个概率分布。而这样的转换核对应唯一的收敛概率,即 。(即满足这个式子的分布就是收敛分布)
如果转换核满足平衡条件 ,p(x)是这个马尔科夫链的收敛概率分布,即长远来看,xi将会逐渐服从p(x)。因为 。因此,MH的转换核满足平衡条件,所以抽样得到的样本将会趋向于p(x)。
因为算法内部有拒绝的设定,所以不存在死循环(即每一次产生一个新的proposal x*,都有机会移动到该值上)。为了证明MH算法不存在可简化性,需要证明在有限步内x的每一个取值都有正的概率。
MH算法有两个简易的特例:Independent Sampler和Metropolis Algorithm。
- Independent Sampler使用的q(x*|x)=q(x*),即独立于当前实现值。所以,w(x)就是前面重要性抽样里的重要性权重。这个方法类似重要性抽样,但是这个方法的样本是相关的。
- Metropolis Algorithm:使用对称的随机游走(random walk)参考分布q,q(x*|x)=q(x|x*),所以
另外,MH算法有几个重要性质:
- 目标分布p(x)的标准化常数不需要知道;
- 可以改进前面的伪代码实现同时制作多条链;
- 对q的选择决定了MH是否可以成功。
------------------接下去就是MCMC如何解决具体问题-----------------
- 寻找p(x)最大值(simulated annealing)
即通过MCMC寻找p(x)的众数。单纯地使用效率很低,因为在远离众数的区间浪费太多计算资源。这里介绍一种模拟退火(simulated annealing)方法,即对前述MCMC作出调整,使得其不在收敛于p(x)而是,其中Ti是一个冷却因子,随着i不断增大,其趋向于0。依据是的图像将会集中在p(x)最大值处。而方法的成败受到q和T的影响。伪代码如下:
1. 随便整一个x0,比如都为0,另T0=1
2. for i = 0 to N-1:
产生一个服从均匀分布的变量u
产生一个服从q(x*|x)的变量x*
如果u效果如图:
- 转换核的混搭和循环
MCMC还有一个优点就是可以结合多种抽样器于一个混合的(mixture)或循环的(cycle)抽样器。即若K1和K2是具有相同收敛分布p的核,那么循环核K1K2和混搭核vK1+(1-v)K2, ,都是具有收敛分布p的核。
混搭核可以通过一个总体参考分布先探索可能的取值范围,然后再针对不同的抽样器选用不同的参考函数来探索目标分布的性质。这对于有很多极值的目标分布很有效。
循环核可以很好地分离多元变量形成不同组分并分别在算法中更新。循环核应用中有一个很流行的叫做Gibbs抽样,通过使用全条件分布(xi表示第i维的input,即input矩阵的第i列)作为参考概率分布。
- Gibbs 抽样
- Monte Carlo EM
EM(期望-最大化)算法是极大似然点估计的一个标准算法。若X包含显性和隐性变量(不可直接观察值)那么似然率的一个局部最大值可以通过如下两个步骤循环得到:
- E步:基于隐变量计算似然函数的均值
- M步:选取最大化
其中,E步就可以用MCMC来抽取的样本。
- 辅助变量抽样(Auxiliary variable samplers)
有时联合分布比边缘分布好抽样,所以可以先通过联合分布得到样本,然后忽略掉作为辅助的变量。下面介绍两种。
- 混血蒙地卡罗(Hybrid Monte Carlo 无脑直译):通过包含目标分布的梯度信息来提高高维度抽样的效率。下面介绍“青蛙跳”HMC算法:首先假设目标分布p(x)可导。联合分布p(x,u)定义为,再定义梯度向量,以及一个固定的步长。在抽样过程中,每一步中我们都重复L次(自行决定)“青蛙跳”,就是u和x用对方的值进行更新。这般重复后得到的x和u就是提议的样本,进入下一个环节,即“接受-拒绝”考验。L和的选择决定了算法的速度。大的L可以得到与初始值差距很大的提议值,但是算的满。另外,对不同维度的x设置不同的也会提高效率。
- 切片抽样(slice sampler):是Gibbs抽样的一个概括。辅助变量和目标变量组成的联合分布是,所以。条件概率分布为。算法就是基于当前步得到的sample xi,先在0到p(xi)之间均匀抽样一个u,然后在p(x)>u的区域A内均匀抽样一个x。
- 可逆跳跃MCMC(Reversible jump MCMC)(最新补充)
涉及模型选择问题,如选择神经网络的神经元个数、多元自适应Spline回归的splines个数、或者时间序列自回归模型的延后期(lag)个数、以及最优的输入数据集。
给定一类模型集合M,我们将构建遍历马尔科夫链(ergodic markov china),使得其收敛分布为p(m,xm)。可以实现模拟以及对比不同维度的分布。
遍历马尔科夫链:若马尔科夫链上的每一个状态(state)都是可遍历的,那么这个MC就是一个EMC,其实就是具有不可化简性,可以从任何状态到达任何状态。根据Yanan Fan and Scott A. Sisson的Paper Reversible Jump Markov chain MonteCarlo ,MH算法是Reversible jump MCMC是的一个特殊形式,后者可以应用于更多状态空间。
给定一个模型集合M={M1,M2,...,Mk},k表示模型参数的一个代号,具体对应于一个模型M,代号k的参数是是一个多维参数向量。所以基于观测值x,(k,)的后验分布可以通过贝叶斯方法得到,分母就是观测值的非条件概率(基于所有可能的模型和所有可能的参数)。RJ-MCMC就是用这个联合后验分布作为MCMC的收敛分布,且该马尔科夫链的状态空间是,即每一个状态长(k,)这样。因此,通过单个马尔科夫链,可以得到基于观测值的完整后验概率,以及单个模型的后验分布。
具体的实现如下:
给定初始的k和theta_k,
for i = 1 to N:
模型内移动:在模型k内,用参考分布抽样一个新的参数向量theta_k
模型间跳动:根据预设的接受概率,在不同模型间移动,即同时更新k和theta_k
MCMC的前沿研究
- 收敛速度
希望找到一个界限,使得在该步以后MC基本收敛。
- 自适应MCMC
在抽样过程中根据抽取的样本调整参考分布,不过目前的研究都没有显著效果
- Sequential Monte Carlo and particle filters
适用于连续型数据分析,例如信号等。
- 机器学习领域
主要应用在高维度模型,大数据。
----------------------------------以下是附录----------------------------------
Code 1 Rejection Sampling
import numpy as np
import matplotlib.pyplot as plt
import math
def p(x):
#standard normal
mu=0
sigma=1
return 1/(math.pi*2)**0.5/sigma*np.exp(-(x-mu)**2/2/sigma**2)
#uniform proposal distribution on [-4,4]
def q(x): #uniform
return np.array([0.125 for i in range(len(x))])
x = np.linspace(-4,4,500)
M = 3.5
N=1000 #number of samples needed
i = 1
count = 0
X = np.array([])
while i < N:
u = np.random.rand(10) #evaluate 10 each loop
x = (np.random.rand(10)-0.5)*8
res = u < p(x)/q(x)/M
if any(res):
X = np.hstack((X,x[res]))
i+=len(x[res])
count+=10
count -= len(X) - 1000
X=X[:1000]
x = np.linspace(-4,4,500)
plt.plot(x,p(x))
plt.hist(X,bins=100,normed=True)
plt.title('Rejection Sampling')
print N/count #proportion of raw sample used
Code 2: Sampling Importance Resampling
import numpy as np
import matplotlib.pyplot as plt
def p(x):
#standard normal
mu=0
sigma=1
return 1/(math.pi*2)**0.5/sigma*np.exp(-(x-mu)**2/2/sigma**2)
#uniform proposal distribution on [-4,4]
def q(x): #uniform
return np.array([0.125 for i in range(len(x))])
#draw N samples that conform to q(x), and then draw M from then that approximately conform to p(x)
N=100000
M=1000
x = (np.random.rand(N)-0.5)*8
w_x = p(x)/q(x)
w_x = w_x/sum(w_x)
w_xc = np.cumsum(w_x) #used for uniform quantile inverse
# resample from x with replacement with probability of w_x
X=np.array([])
for i in range(M):
u = np.random.rand()
X = np.hstack((X,x[w_xc>u][0]))
x = np.linspace(-4,4,500)
plt.plot(x,p(x))
plt.hist(X,bins=100,normed=True)
plt.title('Sampling Importance Resampling')
Code 3: Metropolis_Hastings for MCMC
def q(x_star,x):
#normal distribution
mu=x
sigma=10
return 1/(math.pi*2)**0.5/sigma*np.exp(-(x_star-mu)**2/2/sigma**2)
def p(x): #target distribution
return 0.3*np.exp(-0.2*x**2)+0.7*np.exp(-0.2*(x-10)**2)
N = [100,500,1000,5000]
fig = plt.figure()
for i in range(4):
X = np.array([])
x = 0.1 #initialize x0 to be 0.1
for j in range(N[i]):
u = np.random.rand()
x_star = np.random.normal(x,10)
A = min(1,p(x_star)*q(x,x_star)/p(x)/q(x_star,x))
if u < A:
x = x_star
X=np.hstack((X,x))
ax = fig.add_subplot(2,2,i+1)
ax.hist(X,bins=100,normed=True)
x = np.linspace(-10,20,5000)
ax.plot(x,p(x)/2.7) #2.7 is just a number that approximates the normalizing constant
ax.set_ylim(0,0.35)
ax.text(-9,0.25,'I=%d'%N[i])
fig.suptitle('Metropolis_Hastings for MCMC')
Reference
- CHRISTOPHE, NANDO, ARNAUD, MICHAEL(2003) An Introduction to MCMC for Machine Learning
- Yanan Fan and Scott A. Sisson (2010) Reversible Jump Markov chain MonteCarlo