Learning to rank总结

一、Ranknet

在使用搜索引擎的过程中，对于某一Query(或关键字)，搜索引擎会找出许多与Query相关的URL，然后根据每个URL的特征向量对该URL与主题的相关性进行打分并决定最终URL的排序，其流程如下：

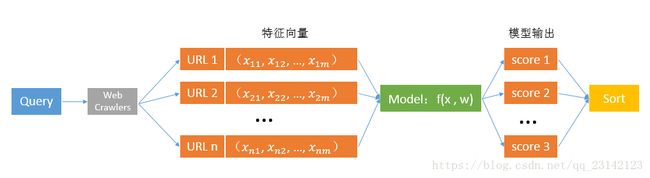
排序的好坏完全取决于模型的输出，而模型又由其参数决定，因而问题转换成了如何利用带label的训练数据去获得最优的模型参数w。Ranknet提供了一种基于Pairwise的训练方法。

1、Cost function

预测相关性概率

对于任意一个URL对(Ui,Uj)，模型输出的score分别为si和sj，那么根据模型的预测，Ui比Uj与Query更相关的概率为 Pij=P(Ui>Uj)=11+e−σ(si−sj) P i j = P ( U i > U j ) = 1 1 + e − σ ( s i − s j ) ，其中 σ σ 是个参数。

真实相关性概率

定义真实相关性概率为 Pij⎯⎯⎯⎯⎯⎯=12(1+Sij) P i j ¯ = 1 2 ( 1 + S i j ) ，对于训练数据中的Ui和Uj，它们都包含有一个与Query相关性的真实label，如果Ui比Uj更相关，那么Sij=1；如果Ui不如Uj相关，那么Sij=−1；如果Ui、Uj与Query的相关程度相同，那么Sij=0。

代价函数定义

C(Pij⎯⎯⎯⎯⎯⎯,Pij) C ( P i j ¯ , P i j )

=−∑Ui>Uj,Ui<Uj,Ui=UjPij⎯⎯⎯⎯⎯⎯logPij = − ∑ U i > U j , U i < U j , U i = U j P i j ¯ l o g P i j

=−Pij⎯⎯⎯⎯⎯⎯logPij−(1−Pij⎯⎯⎯⎯⎯⎯)log(1−Pij)−12log12 = − P i j ¯ l o g P i j − ( 1 − P i j ¯ ) l o g ( 1 − P i j ) − 1 2 l o g 1 2

=−Pij⎯⎯⎯⎯⎯⎯logPij−(1−Pij⎯⎯⎯⎯⎯⎯)log(1−Pij) = − P i j ¯ l o g P i j − ( 1 − P i j ¯ ) l o g ( 1 − P i j )
化简如下：

下图展示了 Cij C i j 随 Pij⎯⎯⎯⎯⎯⎯、Pij P i j ¯ 、 P i j 的变化情况：

图中t表示 si−sj s i − s j ，可以看到当 Sij=1 S i j = 1 时，模型预测的 si比sj s i 比 s j 越大，其代价越小； Sij=−1 S i j = − 1 时， si s i 比 sj s j 越小，代价越小； Sij=0 S i j = 0 时，代价的最小值在 si s i 与 sj s j 相等处取得。该代价函数有以下特点：
1)当两个相关性不同的文档算出来的模型分数相同时，损失函数的值大于0，仍会对这对pair做惩罚，使他们的排序位置区分开
2)损失函数是一个类线性函数，可以有效减少异常样本数据对模型的影响，因此具有鲁棒性

总代价

C=∑(i,j)∈ICij C = ∑ ( i , j ) ∈ I C i j ，I表示所有URL pair的集合，对于 (i,j)∈I ( i , j ) ∈ I 的pair，i>j，即 Sij=1 S i j = 1 。

2、梯度下降更新模型参数W

wk:=wk−αdCdwk w k := w k − α d C d w k

dCdwk=∑(i,j)∈I(dcijdsidsidwk+dcijdsjdsjdwk) d C d w k = ∑ ( i , j ) ∈ I ( d c i j d s i d s i d w k + d c i j d s j d s j d w k )

dCijdsi=σ(12(1−sij)−11+eσ(si−sj))=−dCijdsj=λij d C i j d s i = σ ( 1 2 ( 1 − s i j ) − 1 1 + e σ ( s i − s j ) ) = − d C i j d s j = λ i j

dCdwk=∑(i,j)∈I(λijdsidwk−λijdsjdwk)=∑(i,j)∈Iλij(dsidwk−dsjdwk) d C d w k = ∑ ( i , j ) ∈ I ( λ i j d s i d w k − λ i j d s j d w k ) = ∑ ( i , j ) ∈ I λ i j ( d s i d w k − d s j d w k )

令 λi=∑j:(i,j)∈Iλij−∑j:(j,i)∈Iλij λ i = ∑ j : ( i , j ) ∈ I λ i j − ∑ j : ( j , i ) ∈ I λ i j

dCdwk=∑iλidsjdwk d C d w k = ∑ i λ i d s j d w k

综上 wk:=wk−α∑iλidsjdwk w k := w k − α ∑ i λ i d s j d w k

二、LambdaRank

RankNet以错误pair最少为优化目标，然而NDCG或者ERR等评价指标就只关注top k个结果的排序，所以修改cost function如下。

1、Cost function

Cij=log(1+e−σ(si−sj))|ΔNDCG| C i j = l o g ( 1 + e − σ ( s i − s j ) ) | Δ N D C G |

λij=−σ1+eσ(si−sj)|ΔNDCG| λ i j = − σ 1 + e σ ( s i − s j ) | Δ N D C G |

优化方式与RankNet相似。

三、LambdaMART

以上两个方法都是通过cost function，采用随机梯度下降更新模型参数，使得计算URL的score值在所有URL排序中，属于最优位置。但是lambdamart是用梯度 λij=dCijdsi λ i j = d C i j d s i 建立gradient boosting CART回归树，最后得到回归树的加法模型作为最终模型。下面从简单的模型讲解，一步步推导至lambdaMART。

1、AdaBoost算法

AdaBoost思想就是提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值；加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差率大的弱分类器的权值，使其在表决中起较小作用。

计算第m次迭代训练数据更新的权值 Dm+1 D m + 1

1. 初始化训练数据的权值分布 D1 D 1 为均值：
   D1=(w11,...,w1i,...,w1N),w1i=1N,i=1,2,...,N D 1 = ( w 11 , . . . , w 1 i , . . . , w 1 N ) , w 1 i = 1 N , i = 1 , 2 , . . . , N
2. 第m次迭代的弱分类器 Gm(x) G m ( x ) 在训练数据集上的分类误差率：
   em=P(Gm(xi)≠yi)=∑Ni=1wmiI(Gm(xi)≠yi) e m = P ( G m ( x i ) ≠ y i ) = ∑ i = 1 N w m i I ( G m ( x i ) ≠ y i )
3. 更新训练数据集的权值分布
   Dm+1=(wm+1,1,...,wm+1,i,...,wm+1,N) D m + 1 = ( w m + 1 , 1 , . . . , w m + 1 , i , . . . , w m + 1 , N )
   wm+1,i=wmie−αmyiGm(xi)Zm w m + 1 , i = w m i e − α m y i G m ( x i ) Z m ，i=1,2,..,N， αm α m 为当前迭代的弱分类器的权重。
   Zm Z m 是规范化因子 Zm=∑Ni=1wmie−αmyiGm(xi) Z m = ∑ i = 1 N w m i e − α m y i G m ( x i ) ，规范后使得 Dm+1 D m + 1 成为一个概率分布。
   1）当 Gm(x)=yi G m ( x ) = y i 时， wm+1,i=wmie−αmZm w m + 1 , i = w m i e − α m Z m ，正确分类样本权值缩小
   2）当 Gm(x)≠yi G m ( x ) ≠ y i 时， wm+1,i=wmieαmZm w m + 1 , i = w m i e α m Z m ，错误分类样本权值增大

计算第m次迭代的弱分类器 Gm(x) G m ( x ) 权值 αm α m

Gm(x) G m ( x ) 的权值： αm=12log1−emem α m = 1 2 l o g 1 − e m e m ，对数为自然对数。
其中 1−emem=1em−1 1 − e m e m = 1 e m − 1
1）当 em e m 大， 1−emem 1 − e m e m 小， am a m 小，分类器权重变低
2）当 em e m 小， 1−emem 1 − e m e m 大， am a m 大，分类器权重变高。

算法

输入：训练数据集 T=(x1,y1),(x2,y2),...,(xN,yN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) ，其中 xi∈χ⊆Rn，yi∈y⊆{−1,+1} x i ∈ χ ⊆ R n ， y i ∈ y ⊆ { − 1 , + 1 } ; 弱学习算法；
输出：最终分类器G(x).

1.初始化训练数据的权值分布
D1=(w11,...,w1i,...,w1N),w1i=1N,i=1,2,...,N D 1 = ( w 11 , . . . , w 1 i , . . . , w 1 N ) , w 1 i = 1 N , i = 1 , 2 , . . . , N

2.对m=1,2,…,M
（a）使用具有权值分布 Dm D m 的训练数据集学习，得到基本分类器 Gm(x)，Gm(x):χ G m ( x ) ， G m ( x ) : χ ->{1,-1}

（b）计算 Gm(x) G m ( x ) 在训练数据集上的分类误差率 em=P(Gm(xi)≠yi)=∑Ni=1wmiI(Gm(xi)≠yi) e m = P ( G m ( x i ) ≠ y i ) = ∑ i = 1 N w m i I ( G m ( x i ) ≠ y i )

（c）计算 Gm(x) G m ( x ) 的系数 αm=12log1−emem α m = 1 2 l o g 1 − e m e m ，对数为自然对数

（d）更新训练数据集的权值分布
       Dm+1=(wm+1,1,...,wm+1,i,...,wm+1,N) D m + 1 = ( w m + 1 , 1 , . . . , w m + 1 , i , . . . , w m + 1 , N )
       wm+1,i=wmie−αmyiGm(xi)Zm w m + 1 , i = w m i e − α m y i G m ( x i ) Z m ，i=1,2,..,N
       Zm Z m 是规范化因子 Zm=∑Ni=1wmie−αmyiGm(xi) Z m = ∑ i = 1 N w m i e − α m y i G m ( x i ) ，规范后使得 Dm+1 D m + 1 成为一个概率分布

3.构建基本分类器的线性组合 f(x)=∑Mm=1αmGm(x) f ( x ) = ∑ m = 1 M α m G m ( x ) ，得到最终分类器 G(x)=sign(f(x))=sign(∑Mm=1αmGm(x) G ( x ) = s i g n ( f ( x ) ) = s i g n ( ∑ m = 1 M α m G m ( x ) )

等价算法-前向分步加法算法

当前向分步算法的损失函数是指数函数时，就是AdaBoost算法。也就是说，前项分步加法算法每次直接通过最小化指数损失函数 L(yi,fm−1(xi)+αG(xi))=exp[−yi∗(fm−1(xi)+αG(xi))] L ( y i , f m − 1 ( x i ) + α G ( x i ) ) = e x p [ − y i ∗ ( f m − 1 ( x i ) + α G ( x i ) ) ] ，得到弱分类器的参数和权值 α α ；AdaBoost算法是其具体做法，每次通过带权的训练数据学习弱分类器参数，根据分类误差率计算当前迭代弱分类器的权值 α α 以及训练数据的权值，而训练数据的权值也是为了下一次迭代求弱分类器的参数，目标为了最小化最终分类器的误分率，否则每次训练数据权重一样，每次学出来的分类器都是一样的，改变训练数据权重是为了让不同分类器侧重不同的特征。

1）加法模型

f(x)=∑Mm=1βmb(x;γm) f ( x ) = ∑ m = 1 M β m b ( x ; γ m ) ，其中 b(x;γm) b ( x ; γ m ) 为基函数， γm γ m 为基函数的参数， βm β m 为基函数的系数。

在给定训练数据及损失函数 L(y,f(x)) L ( y , f ( x ) ) ，通过最小化损失函数 minβ,γ∑Ni=1L(yi,βmb(xi;γm)) m i n β , γ ∑ i = 1 N L ( y i , β m b ( x i ; γ m ) ) 学习加法模型f(x)。

2）前向分步算法

输入：训练数据集 T=(x1,y1),(x2,y2),...,(xN,yN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) ；损失函数 L(y,f(x)) L ( y , f ( x ) ) ；基函数集 {b(x;γ)} { b ( x ; γ ) } ;
输出：加法模型f(x)

1. 初始化 f0(x)=0 f 0 ( x ) = 0

2. 对m=1,2,…,M

（a）极小化损失函数 (βm,γm)=argminβ,γ∑Ni=1L(yi,fm−1(xi)+βb(xi;γ)) ( β m , γ m ) = a r g m i n β , γ ∑ i = 1 N L ( y i , f m − 1 ( x i ) + β b ( x i ; γ ) ) ，得到参数 βm,γm β m , γ m

（b）更新 fm(x)=fm−1(x)+βmb(x;γm) f m ( x ) = f m − 1 ( x ) + β m b ( x ; γ m )

3. 得到加法模型 f(x)=fM(x)=∑Mm=1βmb(x;γm) f ( x ) = f M ( x ) = ∑ m = 1 M β m b ( x ; γ m )

3）由指数损失的前向分步算法推导至AadBoost

假设经过m-1轮迭代，前向分步算法已经得到 fm−1(x) f m − 1 ( x ) ，第m轮迭代目标是得到 αm、Gm(x) α m 、 G m ( x ) ，然后得到 fm(x)=fm−1(x)+αmGm(x) f m ( x ) = f m − 1 ( x ) + α m G m ( x ) ,使得 fm(x) f m ( x ) 在训练数据集上的指数损失最小，损失函数为： L(yi,fm(x))=∑Ni=1exp[−yi(fm−1(xi)+αG(xi))] L ( y i , f m ( x ) ) = ∑ i = 1 N e x p [ − y i ( f m − 1 ( x i ) + α G ( x i ) ) ] 。

即 (αm,Gm(x))=argminα,G∑Ni=1exp[−yi(fm−1(xi)+αG(xi))] ( α m , G m ( x ) ) = a r g m i n α , G ∑ i = 1 N e x p [ − y i ( f m − 1 ( x i ) + α G ( x i ) ) ]

化简，令 w⎯⎯⎯⎯mi=exp[−yifm−1(xi)] w ¯ m i = e x p [ − y i f m − 1 ( x i ) ]

得到 (αm,Gm(x))=argminα,G∑Ni=1w⎯⎯⎯⎯miexp[−yiαG(xi)] ( α m , G m ( x ) ) = a r g m i n α , G ∑ i = 1 N w ¯ m i e x p [ − y i α G ( x i ) ]

（1)求 Gm(x) G m ( x )

对任意 α⪈0 α ⪈ 0 ， Gm(x)=argminG∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi)) G m ( x ) = a r g m i n G ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) ，即AdaBoost的基本分类器。

（2）求 α α

L=∑Ni=1w⎯⎯⎯⎯miexp[−yiαG(xi)] L = ∑ i = 1 N w ¯ m i e x p [ − y i α G ( x i ) ]

=∑yi=Gm(xi)w⎯⎯⎯⎯mie−α+∑yi≠Gm(xi)w⎯⎯⎯⎯mieα = ∑ y i = G m ( x i ) w ¯ m i e − α + ∑ y i ≠ G m ( x i ) w ¯ m i e α

=e−α(∑Ni=1w⎯⎯⎯⎯mi−∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi)))+eα(∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))) = e − α ( ∑ i = 1 N w ¯ m i − ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) ) + e α ( ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) )

=(eα−e−α)∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))+e−α∑Ni=1w⎯⎯⎯⎯mi = ( e α − e − α ) ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) + e − α ∑ i = 1 N w ¯ m i

令 dLdα=0 d L d α = 0

(eα+e−α)∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))−e−α∑Ni=1w⎯⎯⎯⎯mi=0 ( e α + e − α ) ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) − e − α ∑ i = 1 N w ¯ m i = 0

(eα+e−α)∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))=e−α∑Ni=1w⎯⎯⎯⎯mi ( e α + e − α ) ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) = e − α ∑ i = 1 N w ¯ m i

(eα+e−α)e−α=∑Ni=1w⎯⎯⎯⎯mi∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi)) ( e α + e − α ) e − α = ∑ i = 1 N w ¯ m i ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) )

e2α=∑Ni=1w⎯⎯⎯⎯mi∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))−1 e 2 α = ∑ i = 1 N w ¯ m i ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) − 1

α=12log[∑Ni=1w⎯⎯⎯⎯mi∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))−1] α = 1 2 l o g [ ∑ i = 1 N w ¯ m i ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) − 1 ]

其中 em=∑Ni=1w⎯⎯⎯⎯miI(yi≠G(xi))∑Ni=1w⎯⎯⎯⎯mi e m = ∑ i = 1 N w ¯ m i I ( y i ≠ G ( x i ) ) ∑ i = 1 N w ¯ m i ,为分类误差率，分错的样本加权求和除以总的样本加权求和。

α=12log(1em−1)=12log(1−emem) α = 1 2 l o g ( 1 e m − 1 ) = 1 2 l o g ( 1 − e m e m ) ,即AdaBoost算法的分类器权重计算方式。

（3)更新每轮样本权值

由 fm(x)=fm−1(x)+αmGm(x) f m ( x ) = f m − 1 ( x ) + α m G m ( x ) , w⎯⎯⎯⎯m,i=exp[−yifm−1(xi)] w ¯ m , i = e x p [ − y i f m − 1 ( x i ) ] ，可知

w⎯⎯⎯⎯m+1,i=exp[−yifm(xi)] w ¯ m + 1 , i = e x p [ − y i f m ( x i ) ]

=exp[−yi(fm−1(xi)+αmGm(xi))] = e x p [ − y i ( f m − 1 ( x i ) + α m G m ( x i ) ) ]

=w⎯⎯⎯⎯m,iexp[−yiαmGm(xi))] = w ¯ m , i e x p [ − y i α m G m ( x i ) ) ] ,即AdaBoost算法训练数据权值更新的计算方式，但此处权值归一化放在了 em e m 计算时。

综上，指数损失的前向分步算法就是AdaBoost算法。

2、CART回归树

CART是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法，一般为二叉树，递归的二分每个特征。

算法

输入：训练数据集D；
输出：回归树f(x)
1. 遍历所有的j和s，选择最优切分变量j（特征）与切分点s（特征值），即求解 minj,s[minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2] m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ]
【 c1 c 1 是所有划分到 R1 R 1 区域的样本的 yi y i 的均值】

2. 用选定的对(j,s)划分区域并决定相应的输出值：
R1(j,s)=x|x(j)≤s,R2(j,s)=x|x(j)⪈s R 1 ( j , s ) = x | x ( j ) ≤ s , R 2 ( j , s ) = x | x ( j ) ⪈ s

cm=1Nm∑xi∈Rm(j,s)yi c m = 1 N m ∑ x i ∈ R m ( j , s ) y i

3. 继续对两个子区域调用步骤1、2，直至满足停止条件

4. 将输入空间划分为M个区域 R1,R2,...,RM R 1 , R 2 , . . . , R M (即M个叶子节点)，生成决策树： f(x)=∑Mm=1cmI(x∈Rm) f ( x ) = ∑ m = 1 M c m I ( x ∈ R m ) ，判断样本属于哪个叶子节点，输出就赋值该叶子节点的均值。

3、提升树(AdaBoost+CART)

提升树模型就是决策树的加法模型，对于分类问题，损失函数为指数损失函数，故只需要将AdaBoost算法中的分类器限定为二类分类树即可，也就是说分类提升树就是AdaBoost的一个特例。而对于回归提升树， fM(x)=∑Mm=1T(x;Θm) f M ( x ) = ∑ m = 1 M T ( x ; Θ m ) ，其中， T(x;Θm) T ( x ; Θ m ) 表示决策树， Θm Θ m 为决策树的参数；M为树的个数。由于是回归模型，此处默认所有基函数参数为1。

若将输入空间划分成J个互不相交的区域 R1,R2,...,RJ R 1 , R 2 , . . . , R J (即决策树的叶子节点)，并在每个区域上确定输出常量 cj c j ，决策树可表示为 T(x;Θm)=∑Jj=1cjI(x∈Rm)，Θm={(R1,c1),(R2,c2),...,(RJ,cJ)} T ( x ; Θ m ) = ∑ j = 1 J c j I ( x ∈ R m ) ， Θ m = { ( R 1 , c 1 ) , ( R 2 , c 2 ) , . . . , ( R J , c J ) } 。

采用平方误差损失函数
L(y,f(x))=(y−f(x))2=[y−fm−1(x)−T(x;Θm)]2 L ( y , f ( x ) ) = ( y − f ( x ) ) 2 = [ y − f m − 1 ( x ) − T ( x ; Θ m ) ] 2 ，为了让损失函数最小，只需要让 T(x;Θm) T ( x ; Θ m ) 接近前一次迭代的加法模型输出与真实输出的残差 r=y−fm−1(x) r = y − f m − 1 ( x ) 。

综上，对回归问题的提升树算法来说，最小化损失函数只需要简单地拟合当前模型的残差。

算法

输入：训练数据集 T=(x1,y1),(x2,y2),...,(xN,yN) T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) ，其中 xi∈χ⊆Rn，yi∈y⊆R x i ∈ χ ⊆ R n ， y i ∈ y ⊆ R ;
输出：提升树 fM(x) f M ( x )

1. 初始化 f0(x)=0 f 0 ( x ) = 0

2. 对m=1,2,…,M

（a）计算残差 rmi=yi−fm−1(xi) r m i = y i − f m − 1 ( x i )

（b）拟合残差 rmi r m i 学习一个回归树，得到第m棵树的叶节点区域 Rmj R m j ，j=1,2,…,J

（c）对j=1,2,…,J，计算叶子节点的输出 cmj=ave(yi|xi∈Rmj) c m j = a v e ( y i | x i ∈ R m j ) , 得到 T(x;Θm)=∑Jj=1cmjI(x∈Rmj) T ( x ; Θ m ) = ∑ j = 1 J c m j I ( x ∈ R m j )

（d）更新