O(n^2)时间复杂度的算法 学习笔记三 希尔排序

希尔排序

希尔排序是插入排序的一个变种，利用了插入排序在近乎有序时能高效排序的特性。
思路：
将一个数组分成多个小数组，对一个数组进行插入排序，最后对近乎有序的整个数组进行最后一趟排序。
其中分成多少个子数组，即gap取多少对排序效率有影响。

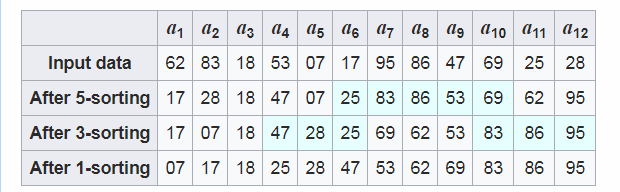
维基百科上的例子：
使用了gap为5,3,1的排序结果。
gap = 5时，对5个分开的子集 (a1, a6, a11), (a2, a7, a12), (a3, a8), (a4, a9), (a5, a10)分别使用插入排序，把子集为(a1, a6, a11) 的 (62, 17, 25)排序为(17, 25, 62).
gap = 3时，对3个分开的子集 (a1, a4, a7, a10), (a2, a5, a8, a11), (a3, a6, a9, a12)分别使用插入排序。
gap = 1时， 对整个数组进行最后一次插入排序。

希尔排序的实现

实现排序算法的时候如何通过索引巧妙地划分成小数组是关键。
第一次gap的常规取值是取floor(n/2)，然后每次gap = floor(gap/2).

for (gap=n/2; gap > 0; gap /= 2){

}

对小数组使用插入排序：
普通的插入排序，在第二轮循环中对，每次将索引为$j$的值与$j-1$进行比较，如下面代码所示

template <typename T>
void insertSort(T arr[], int n){
    for (int i=1; i<n; i++){
        for (int j=i; j>0 && arr[j-1] > arr[j]; j--)
             swap(arr[j-1], arr[j]);
    }
}

直接通过索引值就能到达对每个小数组进行排序的效果。因为数组是按照gap划分为gap个小数组，gap的取值就是分组数目。
对每个小数组进行排序，也就是第二轮循环

 for(i=0; i< gap; i++){}

但是在shell排序中，我们并不会真的先将一个大数组先切分成m个小数组，再使用一个for循环对这m个数组进行m次排序。
因为会有额外的空间开销，更多额外的操作造成效率低下。
那么如上述的例子，当gap为5时，5个子集(a1, a6, a11), (a2, a7, a12), (a3, a8), (a4, a9), (a5, a10)，每个子集的索引都是有规律的。

• 每个子数组的第一个元素的索引值为0
• 通过第一个索引和gap推得子集每个元素的索引。如跟a1同在一个子集的第二个元素的索引a6等于a1加上gap，第三个元素索引为a1加上2*gap或者a6加上gap。

对于第一子数组，按照插入排序的做法，比较a1, a6的索引值，如果a1上的值大于a6上的值，则交换两个位置上的值。

for (int i=1; i<n; i++){
        for (int j=i; j>0 && arr[j-1] > arr[j]; j--)
             swap(arr[j-1], arr[j]);

通过上述的规律，将常规的插入排序的循环修改：

 for (j = i + gap; j < n; j += gap){
       for (int k = j; k > i && arr[k] < arr[k-gap]; k -= gap){
           swap(arr[k - gap], arr[k]);

也可以理解一般的插入排序的gap是1，每次都是相邻两个元素比较。

第一轮循环，选择gap：for (gap=n/2; gap > 0; gap /= 2){}
第二轮循环，对子数组循环：for(i=0; i< gap; i++){}
第三轮循环：插入排序

 for (j = i + gap; j < n; j += gap){
       for (int k = j; k > i && arr[k] < arr[k-gap]; k -= gap){
           swap(arr[k - gap], arr[k]);

这里的边界条件还是需要考虑清楚，比如为什么 k > i。

完整实现：

void shellSort(int arr[], int n) {
    int i, j, gap;
    for (gap = n / 2; gap > 0; gap /= 2) {
        for (i = 0; i < gap; i++) {
            for (j = i + gap; j < n; j += gap){
                for (int k = j; k > i && arr[k] < arr[k-gap]; k -= gap){
                    swap(arr[k-gap], arr[k]);
                }
            }
        }
    }
}

在线调试： 这里

改进算法

减少交换次数, 也就是插入排序的改进。

void shellSort1(int arr[], int n){
    int i, j ,gap;
    for (gap=n/2; gap > 0; gap /= 2){
        for(i = 0; i < gap; i++){
            for (j = i+gap; j<n; j += gap){
                int tmp = arr[j];
                int k;
                for(k = j; k > i && arr[k-gap] > tmp; k -= gap)
                    arr[k] = arr[k-gap];
                arr[k] = tmp;
            }
        }
    }
}

进一步优化

使代码更加简洁，参考刘宇波老师的代码。
这里实现使用的gap=3；

// from liuyubobobo
void shellSort2(int arr[], int n){
	// 计算 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
    int h = 1;
    while(h < n/3)
        h = 3 * h + 1;

    while(h >= 1){
        for(int i = h; i < n; i++){
        	// 对 arr[i], arr[i-h], arr[i-2*h], arr[i-3*h]... 使用插入排序
            int cur = arr[i];
            int j;
            for (j = i; j >= h && arr[j - h] > cur; j -= h)
                arr[j] = arr[j - h];
            arr[j] = cur;
        }
        h /= 3;
    }
}

对比三个算法的排序效率

#include 
#include "SortTestHelper.h"

using namespace std;

void shellSort0(int arr[], int n) {
    int i, j, gap;
    for (gap = n / 2; gap > 0; gap /= 2) {
        for (i = 0; i < gap; i++) {
            for (j = i + gap; j < n; j += gap){
                for (int k = j; k > i && arr[k] < arr[k-gap]; k -= gap){
                    swap(arr[k-gap], arr[k]);
                }
            }
        }
    }
}

void shellSort1(int arr[], int n){
    int i, j ,gap;
    for (gap=n/2; gap > 0; gap /= 2){
        for(i = 0; i < gap; i++){
            for (j = i+gap; j<n; j += gap){
                int tmp = arr[j];
                int k;
                for(k = j; k > i && arr[k-gap] > tmp; k -= gap)
                    arr[k] = arr[k-gap];
                arr[k] = tmp;
            }
        }
    }
}

// from liuyubobobo
void shellSort2(int arr[], int n){
    int h = 1;
    while(h < n/2)
        h = 2 * h + 1;

    while(h >= 1){
        for(int i = h; i < n; i++){
            int cur = arr[i];
            int j;
            for (j = i; j >= h && arr[j - h] > cur; j -= h)
                arr[j] = arr[j - h];
            arr[j] = cur;
        }
        h /= 2;
    }
}


int main() {
//    int arr[15] = {4, 6, 3, 2, 1, 5, 10, 6, 12, 9, 11, 15, 13, 18, 20};
    int n = 1000000;
    int *arr = SortTestHelper::genRandomArray(n, 0, n);
    int *arr1 = SortTestHelper::copyArray(arr, n);
    int *arr2 = SortTestHelper::copyArray(arr, n);
    SortTestHelper::testSort("shellsort0", shellSort0, arr, n);
    SortTestHelper::testSort("shellsort1", shellSort1, arr1, n);
    SortTestHelper::testSort("shellsort2", shellSort2, arr2, n);
    return 0;
}

结果：

D:\cpp_projects\shell_sort\cmake-build-debug\shell_sort.exe
shellsort0 0.691 s
shellsort1 0.32 s
shellsort2 0.35 s

shellsort0 0.061 s
shellsort1 0.086 s
shellsort2 0.065 s

百万级的数量排序也小于1s，对于近乎有序的数组，效率更高，不足0.1s。

取不同的gap对效率的影响

取gap为2,3,5时, 百万量级的排序结果：

// random array
shellsort2 0.341 s
shellsort3 0.333 s
shellsort4 0.313 s

// nearly order array
shellsort2 0.064 s
shellsort3 0.067 s
shellsort4 0.029 s

简答分析得到，当gap越大时，效率越高。但是当gap达到一定程度时不知道效率会不会有所下降。
因为gap越大，可以切分成更多的子数组，每个子数组的长度就越小。
子数组的长度就越小，约近乎有序，而插入排序对于几乎有序的数组效率越高。

关于步长序列的选择

参考 Wikepedia

最好的步长序列是由Sedgewick提出的(1, 5, 19, 41, 109,…)，序列的项来自
$$9\times 4^i-9\times 2^i+1$$
$$2^{i+2}\times (2^{i+2}-3)+1$$