图解堆排序

原文出自公众号程序员小灰：https://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw==&mid=2653195208&idx=1&sn=e3d6559402148458f0a4993b47d8bc6f&chksm=8c99f912bbee7004625a0b204acc8484acbdf4f1b18953e7ff5acbea958ec002d8c8ea072792&mpshare=1&scene=1&srcid=0918puhyPLKbZLQaYEvFO8zu#rd

在了解堆排序之前让我们回顾一下二叉堆和最大堆的特性：

• 1.二叉堆本质上是一种完全二叉树
• 2.最大堆的堆顶是整个堆中的最大元素

首先一定要明确！！！
二叉堆虽然是一个完全二叉树，但它的存储方式并不是链式存储，而是顺序存储。换句话说，二叉堆的所有节点都存储在数组中。

在数组中，在没有左右指针的情况下，如何定位一个父节点的左孩子和右孩子呢？

可以依靠数组下标来计算。
假设父节点的下标是parent，那么它的左孩子下标就是 2 * parent + 1；右孩子下标就是 2 * parent + 2。

当我们删除一个最大堆的堆顶（并不是完全删除，而是替换到最后面），经过自我调节，第二大的元素就会被交换上来，成为最大堆的新堆顶。

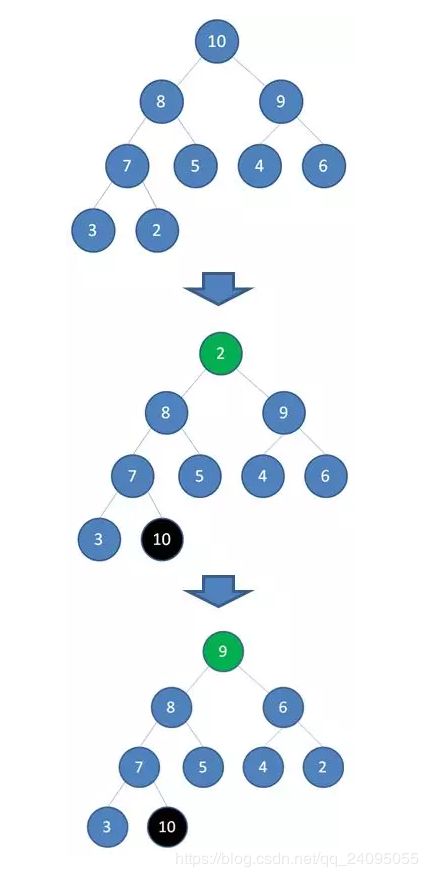
正如上图所示，当我们删除值为10的堆顶节点，经过调节，值为9的新节点就会顶替上来；当我们删除值为9的堆顶节点，经过调节，值为8的新节点就会顶替上来…

由于二叉堆的这个特性，我们每一次删除旧堆顶，调整后的新堆顶都是大小仅次于旧堆顶的节点。那么我们只要反复删除堆顶，反复调节二叉堆，所得到的集合就成为了一个有序集合，过程如下：

删除节点9，节点8成为新堆顶：

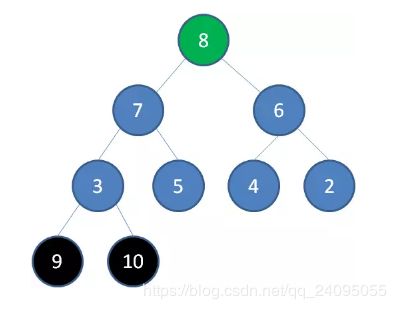
删除节点8，节点7成为新堆顶：

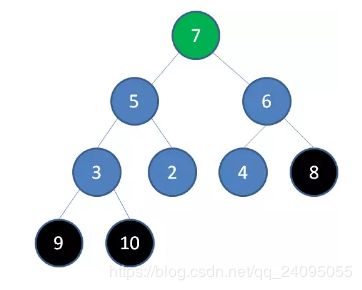
删除节点7，节点6成为新堆顶：

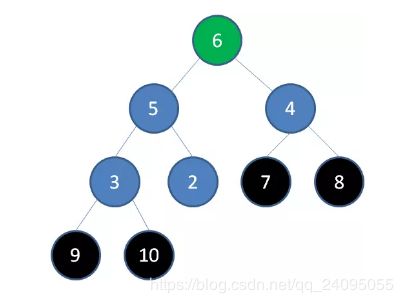
删除节点6，节点5成为新堆顶：

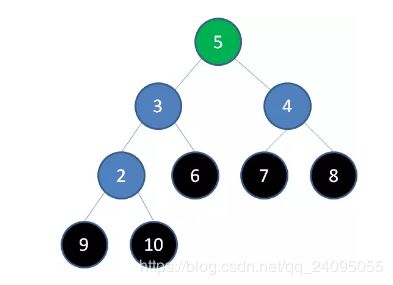
删除节点5，节点4成为新堆顶：

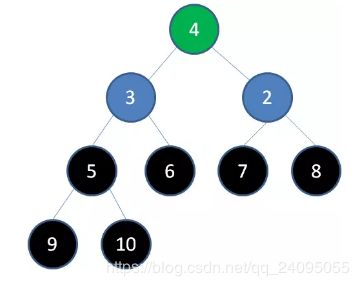
删除节点4，节点3成为新堆顶：

删除节点3，节点2成为新堆顶：

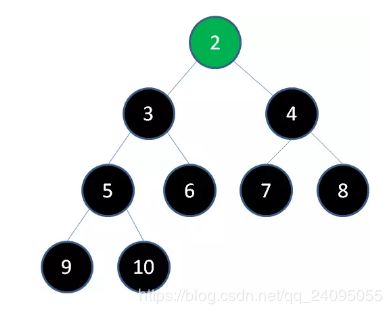
到此为止，我们原本的最大堆已经变成了一个从小到大的有序集合。之前说过二叉堆实际存储在数组当中，数组中的元素排列如下：

由此，我们可以归纳出堆排序算法的步骤：

• 1.把无序数组构建成二叉堆。

• 2.循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

堆排序代码：

import java.util.Arrays;

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = new int[]{1,3,2,6,5,7,8,9,10,0};
        heapSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    /**
     * 堆排序
     * @param arr 待调整的堆
     */
    private static void heapSort(int[] arr) {
        // 1.把无序数组构建成二叉堆
        for (int i = (arr.length - 2)/2; i >= 0 ; i--){
            downAdjust(arr, i, arr.length);
        }
        System.out.println(Arrays.toString(arr));
        // 2.循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶
        for (int i = arr.length - 1; i > 0 ; i--){
            // 最后一个元素和第一元素进行交换
            int temp = arr[i];
            arr[i] = arr[0];
            arr[0] = temp;
            // 下沉调整最大堆 注意这里i是每次减一的，也就达到了“删除”的作用
            downAdjust(arr, 0, i);
        }
    }

    /**
     * 下沉调整
     * @param arr 待调整的堆
     * @param parentIndex 要下沉的父节点
     * @param length 堆的有效大小
     */
    private static void downAdjust(int[] arr, int parentIndex, int length) {
        // temp保存父节点值，用于最后的赋值
        int temp = arr[parentIndex];
        int childIndex = 2 * parentIndex + 1;
        while (childIndex < length){
            // 如果有右孩子，且右孩子大于左孩子的值，则定位到右孩子
            if (childIndex + 1 < length && arr[childIndex + 1] > arr[childIndex]) {
                childIndex ++;
            }
            // 如果父节点小于任何一个孩子的值，直接跳出
            if (temp >= arr[childIndex]) {
                break;
            }
            // 交换父节点与较大节点的值  这里原文只将子节点的值付给父节点  不大理解  我们改为了交换
            int temp1 = arr[parentIndex];
            arr[parentIndex] = arr[childIndex];
            arr[childIndex] = temp1;
            // 子节点成为新的父节点  子子节点成为新的子节点 继续递归直到叶子节点
            parentIndex = childIndex;
            childIndex = childIndex * 2 + 1;
        }
        // 下沉的末尾赋值为原本位置的值
        arr[parentIndex] = temp;
    }
}

二叉堆的节点下沉调整（downAdjust 方法）是堆排序算法的基础，这个调节操作本身的时间复杂度是多少呢？

假设二叉堆总共有n个元素，那么下沉调整的最坏时间复杂度就等同于二叉堆的高度，也就是O（logn）。

我们再来回顾一下堆排序算法的步骤：

1. 把无序数组构建成二叉堆。

2. 循环删除堆顶元素，移到集合尾部，调节堆产生新的堆顶。

第一步，把无序数组构建成二叉堆，需要进行n/2次循环（叶子节点不需要处理）。每次循环调用一次 downAdjust 方法，所以第一步的计算规模是 n/2 * logn，时间复杂度 O（nlogn）。

第二步，需要进行n-1次循环。每次循环调用一次 downAdjust 方法，所以第二步的计算规模是 （n-1） * logn ，时间复杂度 O（nlogn）。

两个步骤是并列关系，所以整体的时间复杂度同样是 O（nlogn）。