各种查找算法-Java-顺序、二分、二叉排序树查找

顺序查找：

原理：让关键字与队列中的数逐个比较，直到找出与给定关键字相同的数为止。

import java.util.Scanner;

public class OrderSearch {

    public static int orderSearch(int[] arr,int num) {
        int i = 0;
        for( ; i < arr.length ; i++ ){
            if(arr[i] == num )
                return i;
        }
        return -1;
    }
    public static void main(String[] args) {
        Scanner sc1 = new Scanner(System.in);
        System.out.println("请输入已知数组,并用逗号隔开：");
        String inputString = sc1.next();
        String[] stringArray = inputString.split(",");
        int length = stringArray.length;
        int[] data = new int[length];
        for(int i = 0;inew Scanner(System.in);
        System.out.println("请输入你要查找的数：");
        int num = sc2.nextInt();
        if( orderSearch(data,num) == -1)
            System.out.println("原数组不存在该数");
        else
            System.out.println("该数在数组中的索引为："+orderSearch(data,num));

        sc1.close();
        sc2.close();
    }
}

二分查找：

原理： 首先假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

算法要求：必须采用顺序存储结构、必须按关键字大小有序排列。

import java.util.Scanner;

public class BinarySearch {

    //循环实现二分查找
    public static int binarySearch1(int[] arr,int num) {
        if (arr == null || arr.length <= 0) {  
            return -1;  
        } 
        int low = 0;
        int high = arr.length - 1;

        while( low <= high && (low <= arr.length - 1) && (high <= arr.length - 1)){
            int middle = ( high + low ) / 2;
            if( num == arr[middle] )
                return middle;
            else if( num < arr[middle] )
                high = middle - 1;
            else
                low = middle + 1;
        }
        return -1;
    }

    //递归实现二分查找
    public static int binarySearch2(int[] arr,int low,int high,int num) {
        if (arr == null || arr.length <= 0) {  
            return -1;  
        } 
        if( low < high ){
            int mid = ( low + high ) / 2 ;
            if( arr[mid] == num )
                return mid;
            else if ( arr[mid] > num )
                binarySearch2(arr, low, mid - 1, num);
            else 
                binarySearch2(arr, mid + 1, high, num);
        }   
        return -1;
    }

    public static void main(String[] args) {
        Scanner sc1 = new Scanner(System.in);
        System.out.println("请输入已知数组,并用逗号隔开(要求升序排列)：");
        String inputString = sc1.next();
        String[] stringArray = inputString.split(",");
        int length = stringArray.length;
        int[] data = new int[length];
        for(int i = 0;inew Scanner(System.in);
        System.out.println("请输入你要查找的数：");
        int num = sc2.nextInt();

        /*if( binarySearch1(data,num) == -1)
            System.out.println("(循环实现)原数组不存在该数");
        else
            System.out.println("(循环实现)该数在数组中的索引为："+binarySearch1(data,num));*/

        if( binarySearch2(data,0,data.length,num) == -1)
            System.out.println("(递归实现)原数组不存在该数");
        else
            System.out.println("(递归实现)该数在数组中的索引为："+binarySearch2(data,0,data.length,num));

        sc1.close();
        sc2.close();
    }
}

二叉排序树查找：

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：
1、若左子树非空，则左子树上所有结点的键值均<=它的根结点的键值；
2、若右子树非空，则右子树上所有结点的键值均>=它的根结点的键值；
3、左、右子树也分别为二叉排序树；

//二叉树的定义
class BinaryTree{
    int value;
    BinaryTree left;
    BinaryTree right;
    public BinaryTree(int value){
        this.value = value;
    }
}

public class BinarySearchTree {

    static BinaryTree f;
    static BinaryTree root;//指向二叉排序树的根节点

    //二叉排序树的创建
    //左<根<右
    public static void creatBST(BinaryTree root ,int key) {

        BinaryTree newNode = new BinaryTree(key);

        //如果大于根节点的值，则放在右节点
        if(key > root.value){
            if(root.right == null)
                root.right = newNode;
            else
                creatBST(root.right, key);
        }
        //如果小于根节点的值，则放在左节点
        else if(key < root.value){
            if(root.left == null)
                root.left = newNode;
            else
                creatBST(root.left, key);
        }
        //如果等于根节点的值，则已经存在
        else{
            System.out.println("The node " + key + " is already exists");  
            return;
        }
    }

    // 二叉排序树的查找  
    // p:保存root的父节点  key:要查询的值
    public static boolean search(BinaryTree root,int key,BinaryTree p) {
        if(root == null){
            f = p;
            System.out.println(key + "不在此队列中");
            return false;
        }
        else if( key == root.value ){
            f = root;
            System.out.println( key + "在此队列中");  
            return true;
        }
        else if( key < root.value )
            return search(root.left, key, root);
        else 
            return search(root.right, key, root);
    }

    //先序遍历
    public static void preOrder(BinaryTree rt) {
        if( rt != null ){
            System.out.print( rt.value + " " );
            preOrder(rt.left);
            preOrder(rt.right);
        }
    }

    //中序遍历
    public static void inOrder(BinaryTree rt) {
        if( rt != null ){
            inOrder(rt.left);
            System.out.print( rt.value + " " );     
            inOrder(rt.right);
        }
    }

    //后序遍历
    public static void postOrder(BinaryTree rt) {
        if( rt != null ){
            postOrder(rt.left);
            postOrder(rt.right);
            System.out.print( rt.value + " " );
        }
    }

    public static void main(String[] args) {
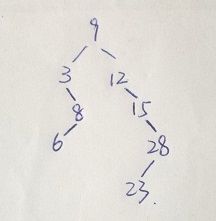
        int[] array = {9,12,15,3,8,28,23,6};
        root = new BinaryTree(array[0]);

        System.out.print("原队列："+ array[0] + " ");
        for( int i = 1; i < array.length ; i++){            
            creatBST(root, array[i]);
            System.out.print( array[i] + " " );
        }
        System.out.println();
        int num = 17;
        System.out.println("查询的数为：" + num);
        search(root, num, null); 

        System.out.print("先序遍历：");
        preOrder(root);
        System.out.println();

        System.out.print("中序遍历：");
        inOrder(root);
        System.out.println();

        System.out.print("后序遍历：");
        postOrder(root);
        System.out.println();
    }
}