python 算法学习笔记1

python中array 是一整块单一连续的内存区域，根据索引值访问的话可以直接计算出目标元素在内存中的位置，对于链表要从头开始遍历
链表插入代价小，数值插入代价大，要移动右边所有的元素
这边的数组指动态数组
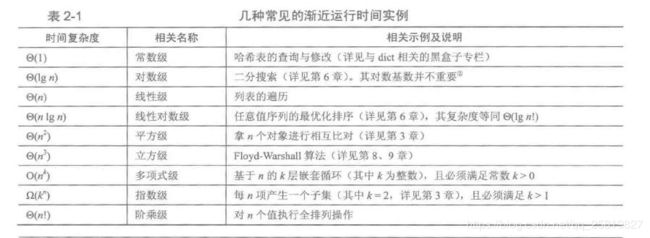
复杂度O

构建排序算法之前先对序列进行检查，如果目标已经排过序则直接返回

def sort_w_check():
    n=len(seq)
    for i in range(n-1):
        if seq[i] >seq[i+1]:
            break
        else:
            return
    ....

排序的三种情况：
1.最好情况，已经排好序，线性时间
2.最坏情况
3.平均情况，期望时间
算法评估：
用timeit模块

import timeit
t1=timeit.timeit("x=2+2")
print(t1)
t2=timeit.timeit("x=sum(range(10))")
print(t2)

计算时间，但对于多次迭代时timeit会通过多次运行相关代码的方式来提高计时精度
图结构：
图的要点主要包括：

散列（hashing）可以通过python中的hash函数提供

print(hash("hello,world!"))
print(hash("Hello,world!"))

python中字典类型dict就是常说的散列表，集合类型也是通过这种机制完成的，
对于散列的访问平局时间为O(1),最坏为O(n)
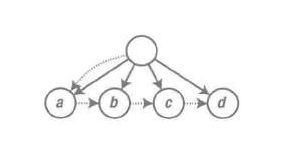
邻接列表及类似的结构
示意图

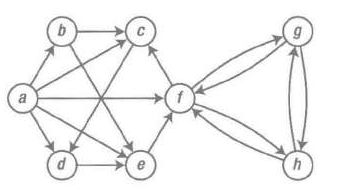
示意图转换为邻接集表示方法

a,b,c,d,e,f,g,h=range(8)
N=[
    {b,c,d,e,f},
    {c,e},
    {d},
    {e},
    {f},
    {c,g,h},
    {f,h},
    {f,g}
]

加权的邻接列表

a,b,c,d,e,f,g,h=range(8)
N=[
    {b:2,c:1,d:3,e:9,f:4},
    {c:4,e:3},
    {d：8},
    {e：7},
    {f：5},
    {c：2,g:2,h:2},
    {f:1,h:6},
    {f:9,g:8}
]

邻接集的字典表示法：

N={
    'a':set('bcdef'),
    'b':set('ce'),
    'c':set('d'),
    'e':set('e'),
    'f':set('cgh'),
    'g':set('fh'),
    'h':set('fg')
}

树
二叉树

class Tree(object):
    """docstring for Tree"""
    def __init__(self, left,right):
        self.left=left
        self.right=right

t=Tree(Tree("a","b"),Tree("c","d"))
print(t.right.left)

多路搜索树

class True:
    def __init__(self,kids,next=None):
        self.kids=self.val=kids
        self.next=next

t=Tree(Tree("a",Tree("b",Tree("c",Tree("d")))))
print(t.kids.next.next.val)

隐性平方级操作
例子

import time
from random import randrange
L=[randrange(10000) for i in range(1000)]
t1=time.time()
print(42 in L)
t2=time.time()
print(t2-t1)
S=set(L)
t3=time.time()
print(42 in S)
t4=time.time()
print(t4-t3)

对list的搜索是线性数量级的，set的搜索是常数级的