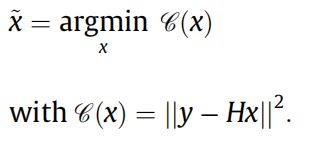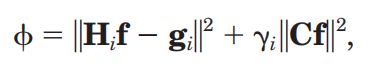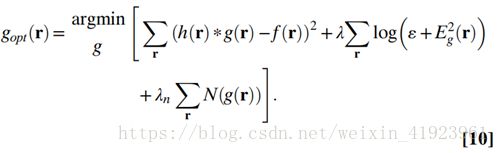【图像处理】【图像去模糊】 总结
本人最近由于做相关去卷积工作,查阅了上百篇文献,发现在这个领域,可能也是‘水太深’了,并没有一篇较好的综述,现在做以下总结----
只对高斯与散焦模糊的非盲去卷积领域,对于运动模糊并未做总结,但实际上除了点扩散函数的估计有区别,实际上这三类去模糊甚至和去噪,损失函数模型都可以通用。
这里对于只做一家之言,如有反对意见请留言指正:
去模糊历史:
1.1970-1990年代用于航天天文领域(Astronaut field);
2.1990-2010年代用于自然图片处理(运动模糊/相机PSF模糊/噪声影响);
3.2010---年代,用于生物成像领域。
到现在为止,无论是否做去卷积领域工作的人,都喜欢在表征结果的时候加一步去卷积步骤,以提升图像分辨率和对比度,使图像易于分析与美观。
综述(模型未统一请见谅):
去卷积领域的水尤其深,对于运动模糊/PSF模糊/噪声/不同成像领域,用法都不尽相同,现只总结在PSF模糊的非相干成像领域的去卷积方法。
实际上只有三种最具有代表性、用的最广的模式,至于其他则是他们的变体:
成像模型:y =Hx + n
其中H为PSF矩阵,x为目标(object),n为加性噪声。
1.Wiener逆滤波
虽然wiener去卷积方法很简单实用,但有时候效果并不好,N往往都是未知量,但由于简单和经典,将其也列在这里,但其实他的变体并不多。
2.Lucy-Richardson(LR)迭代去卷积
1972年Lucy提出的一种基于贝叶斯理论的,现在用处最广最频繁,并且变体最多的一种迭代去卷积方式,由于单纯逆滤波问题的局限性,现在几乎所有的去卷积工作者都利用类似正则化的先验手段,将去卷积问题转化为损失函数,加入正则化惩罚项,类似人工智能的手段,不断迭代寻优,以此达到良好去卷积结果。
LR去卷积假设其符合泊松分布(实际上就是相机接收光子的过程),这是所有成像系统几乎都符合的规则,所以article里多数都是LR的‘忠实粉丝’。利用最大似然估计,得出似然函数,对似然函数-log之后求解最小值的过程,一般采用的最优化方法为EM方法。
实际上很简单:也就是这一模型建立以后:y =K卷积I ,还有一步,即Image=Possion(y)。其假设我们获取得到的图像也就是Image是这一概率分布,则具体方式:
3.基于最小化误差的方法:
可以利用最小二乘以及Landweber迭代法。实际上,3某种程度上也是最大似然估计的一种,在假设图像符合高斯分布的同时,似然函数-log后做近似,可退化成这种模式。
-----------------------------------------------我是分割线------------------------------------------------------------------
加入正则化
插一句:实际上所有迭代算法都要在放大噪声及去卷积结果作为权衡来选择,迭代次数也是一种伪正则手段。
下面说说他们的各种变体:由于图像某种特殊的先验知识,可以对去卷积的损失函数加入惩罚项正则,以约束迭代结果,往往都很成功。首先介绍可以加在2上---LR去卷积,又可以加在3---2范数最小化误差去卷积上的正则法:
1.Tihkonov regularization(TR)
可以看到,这是以3为基础的正则,当然也可以用于2中,这里只做一个说明。有两种形式,一种单纯加入x的2范数做为正则,一种加入Tihkonov矩阵(小波矩阵)C×object,后者通常是高通滤波器,如拉普拉斯滤波器,但在没有进一步先验知识的情况下,可以选择为单位矩阵。这是加入原始图像平滑的先验知识,但是难免造成边缘模糊,(利用小波稀疏的特性抑制。),实际上TR正则在机器学习领域应用也很广。
2.Total Variance (TV正则)
加入的其实是x的一阶偏导数的L1范数正则化,可以很好地保留边缘信息。,为了公平,TV正则是LR+TV正则。
3.L1正则
加入L1为正则,以3为基础,由于L1矩阵可以造成结果的稀疏性,可以很好地抑制背景噪声,但注意系数不要过大,会过度滤除一些信息。
4.小波正则
依旧利用了小波的稀疏性。
5.以上几种正则为基础的各种混合模型。
下面说几个去卷积的最新进展:
1.发表在PNAS上:ER-Decon
2013:High-resolution restoration of 3D structures from widefield images with extreme low signal-to-noise-ratio
利用熵正则,使极低分辨率情况下图像可以得到很好去卷积效果
Huygens是专业去卷积软件,Deconvlab2是EPFL,BIG课题组提供的FIJI去卷积插件。
损失函数:h为PSF,g为目标,f为图像。
2.Nature Biotechnology(Hessian regularization)
2018:Fast, long-term, super-resolution imaging with Hessian structured illumination microscopy
wiener去卷积后得到SIM重建图像g,再对其重建:
3.Nature methods(类似TR正则):
2007:High-resolution threedimensional imaging of large specimens with lightsheet–based microscopy
实际上学习的是TR正则法。