人工智能（python）开发 —— 作用域、闭包以及高级函数和lambda表达式

一、作用域

        作用域也叫命名空间，是访问变量时查找变量名的范围空间

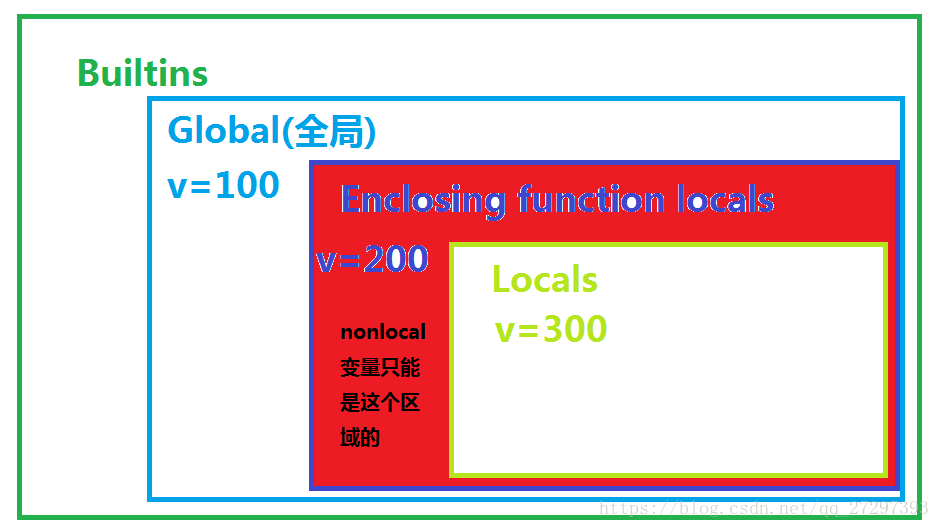
1、python的四个作用域 （LEGB）

作用域	英文解释	英文简写
局部作用域(函数内)	Local(function)	L
外部嵌套函数作用域	Enclosing function locals	E
函数定义所在模块(文件)的作用域	Globals(module)	G
python 内置模块的作用域	Builtin(python)	B

2、变量名的查找规则

          在访问变量时先查找本地变量，然后是包裹此函数外部的函数内部的变量，之后是全局变量,最后是内置(内建)变量
L --->  E  ---> G ---> B
          在默认情况下，变量名赋值会创建或者改变本地作用域变量

3、示例

v = 100
def fun1():
    v = 200
    print('fun1.v = ', v)
    def fun2():
        v = 300
        print('fun2.v=', v)

    fun2()

fun1()
print("全局的v=", v)

4、图示

二、变量作用域声明语句

1、global 语句

作用
        1、告诉解释器,，global语句声明的一个或多个变量，这些变量的作用域为模块级的作用域(也称作全局变量)
        2、全局声明(global) 将赋值的变量映射到模块文件内部的作用域
语法
        global 变量1, 变量2, ...

说明
        1、全局变量如果要在函数内部被赋值,则必须经过全局 声明(否则会被认为是局部变量)
        2、全局变量在函数内部不经过声明就可以直接访问
        3、不能先创建局部变量,再用global声明为全局变量,此做法不附合规则
        4、global变量列表里的变量名不能出现在此作用域内形参列表里

示例
         global v, a, b, c
          global d

示例

v = 100
def fn():
    # 添加全局声明,告诉解释执行器,本函数内的变量v为全局变量
    global v
    v = 200  # 本意想要修改全局变量v让它绑定200

fn()
print("v =", v)

2、nonlocal 语句

作用
          告诉解释器，nonlocal声明的变量不是局部变量，也不是全局变量，而是外部嵌套函数内的变量

语法
          nonlocal  变量名1，变量名2， ...
说明
         1、nonlocal 语句只能在被嵌套的函数内部进行使用
         2、访问nonlocal变量将对外部嵌套函数作用域内的变量进行操作
          3、当有两层或两层以上函数嵌套时，访问nonlocal变量只对最近一层的变量进行操作
          4、nonlocal语句的变量列表里的变量名，不能出现在此函数参数列表中

示例

var = 100
def f1():
    var = 200
    print("f1里的var=", var)
    def f2():
        nonlocal var  # 声明var为f2以外,全局变量以内的变量
        var = 300

    f2()
    print('f1调用结束时var=', var)

f1()
print("全局的var=", var)

图示

        

三、globals/locals 函数

        globals() 返回当前全局作用域内变量的字典
        locals()   返回当前局部作用域内的变量的字典

示例

a = 1
b = 2
c = 3
def fx(c, d):
    e = 300
    # 此处有几个局部变量?
    print('locals() 返回', locals())
    print("globals() 返回", globals())
    print(c)		    # 局部c 100
    print(globals()['c'])   # 全局c 3

fx(100, 200)

四、lambda 表达式

        lambda 表达式(又称匿名函数)

1、作用

        创建一个匿名函数对象
        同 def 类似，但不提供函数名

2、语法格式

        lambda [形参1, 形参2, ...] : 表达式

3、说明

        1、lambda 只是一个表达式，它用来创建一个函数对象
        2、当lambda表达式调用时，先执行冒号(:)后的表达式，并返回表达式的结果的引用
        3、lambda 表达式创建的函数只能包含一条表达式
        4、lambda比函数简单且可以随时创建和销毁，有利于减少程序的偶合度

4、示例

def  myadd（x, y）:
    return x+y
# 可以改写为：
myadd = lambda x，y ： x + y

# 理解一下程序
def fx(f, x, y):
    print(f(x, y))

fx((lambda a, b: a + b), 100, 200) 
fx((lambda a, b: a ** b), 3, 4)

五、高阶函数

1、高阶函数定义

        满足下列条件中一个的函数即为高阶函数
                a、函数接收一个或多个函数作为参数传入
                b、函数返回一个函数

2、map 函数

        map(func, *iterables)

        用函数和对可迭代对象中的每一个元素作为参数返回新的可迭代对象。当最短的一个可迭代对象不再提供数据时迭代结束

要求：func函数接收的参数个数必须与可迭代对象的个数相同

def  power2（x）：
    return  x**2
# 生成一个迭代器，此迭代器可以生成1~9的自然数的平方
# 1 4 6 16
mit = map（power2 ， range（1， 10））
for  x  in  mit：
    print（x）

求 1**2 + 2**2 + 3**2 + ...+ 9**2的和
x = map(lambda x:x**2,range(1,10))
print(sum(x))

求 1**9 + 2**8 + 3**7 + .... + 9**1的和
x = map(lambda x,y:x**y,range(1,10),range(9,0,-1))
print(sum(x))

3、filter 函数

            filter(function, iterable)
            筛选可迭代对象iterable中的数据，返回一个可迭代对象，此可迭代对象将对iterable提供的数据进行筛选
说明：函数function 将对iteralbe中的每个元素进行求布尔值,返回True则保留，返回False则丢弃

def isodd(x):  # 此函数判断x是否为奇数,如果是奇数返回True
    return x % 2 == 1

for x in filter(isodd, range(41, 53)):
    print(x)

4、sorted 函数

        sorted(iterable, key=None, reverse=False)
        将原可迭代对象提供的数据进行排序，生成排序后的列表
说明:
        a、iterable 可迭代对象
        b、key 函数是用来提供一个排序参考值的函数，这个函数的返回值将作为排序的依据
        c、reverse 标志用来设置是否降序排序

L = [5, -2, -4, 0, 3, 1]
L2 = sorted(L)  # [-4, -2, 0, 1, 3, 5]
# 按绝对值排序
L3 = sorted(L, key=abs)  # [0, 1, -2, 3, -4, 5]

names = ['Tom', 'Jerry', 'Spike', 'Tyke']
# 按字符串长度排序 ， 结果 ['Tom', 'Tyke', 'Jerry', 'Spike']
L = sorted(names, key=len)

names = ["tom","jerry","spike","tyke"]
# 按字符串排序的依据为原字符串反序的字符串：'moT', 'yrreJ', 'ekipS', 'ekyT'
# 结果: ['Spike', 'Tyke', 'Tom', 'Jerry']
# 方法1
def xx(a):
     return a[::-1]
print(sorted(names,key=xx))

# 方法2
print(sorted(names,key=lambda x: x[::-1]))

六、递归函数 （recursion）

1、定义

        函数直接或间接的调用自身

2、说明

        递归一定要控制递归的层数，当符合一定条件时要终止递归调用
        几乎所有的递归都能用while循环来代替

3、优点

        递归可以把问题简单化，让思路更为清晰，代码更简洁

4、缺点

        递归因系统环境影响大，当递归深度太大时，可能会得到不可预知的结果

5、递归的两个阶段

        递推阶段:  从原问题出发，按递归公式递推从未知到已知，最终达到递归的终止条件

        回归阶段: 按递归终止条件求出结果，逆向逐步代入递归公式，回归到问题求解

6、递归的实现方法

        先假设函数已经实现

7、示例

# 写一个函数求n的阶乘（递归实现）
def myfac(n):
    if n == 1:
        return 1
    return n * myfac(n-1)

print('5的阶乘是:', myfac(5))

七、闭包 （closure）

        闭包是指引用了此函数外部嵌套函数作用域变量的函数
闭包必须满足三个条件：
        a、必须有内嵌函数
        b、内嵌函数必须引用外部函数中的变量
        c、外部函数返回值必须是内嵌函数

示例：

def make_power(y):
    def fn(x):
        return x ** y
    return fn

pow2 = make_power(2)
print('5的平方是:', pow2(5))

pow3 = make_power(3)
print("6的立方是", pow3(6))

pow100 = make_power(100)
print("2的100次方是:", pow100(2))

八、补充（eval/exec 函数）

1、eval 函数

        eval(source, globals=None, locals=None)
        把一个字符串当成一个表达式来执行，返回表达式执行后的结果
示例

s = input("请输入表达式:")       # 输入100 + 200 * 300
v = eval(s)                     # 等同于 v = 100 + 200 * 300
print("您输入的表达式经过eval执行后结果为", v)

x = 100
y = 200

a = eval("x + y")
print(a)                                                   # 300

local_scope = { "x":5, "y":10}
# a = eval("x+y",globals = None, locals = local_scope)     # 错的,非关键字参数
a = eval("x+y",None,  local_scope)
print("a=",a)                                              # a = 15

z = 300
a = eval("x*y+z",{"z":3333},  local_scope)
print(a) # 3383

2、exec函数

        exec(source, globals=None, locals=None)
        把一个字符串当成'程序'来执行

示例

x = 100
y = 200
s = '''z=x+y
print('z=', z)
print("hello world!")
'''
exec(s)  # 执行 s这个字符串
print(z)

九、附录

        人工智能（python）—— 目录汇总