强化学习论文(1): Soft Actor-Critic

加州伯克利大学发布的 off-policy model-free强化学习算法，soft actor-critic（SAC）
论文地址为：Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
假定已经对经典强化学习建模和基本Actor-Critic方法有所了解。

摘要

模型无关（model-free）深度强化学习算法面临两个主要挑战：高采样复杂度和脆弱的收敛性，因此严重依赖调参，这两个挑战限制了强化学习向现实应用的推广。
在这篇论文中，作者基于最大熵强化学习算法框架，提出了一个off-policy actor-critic 深度强化学习算法。最大熵强化学习要求actor在同时最大化期望和策略分布的熵，也就是说，在保证任务成果的同时希望策略尽可能的随机。
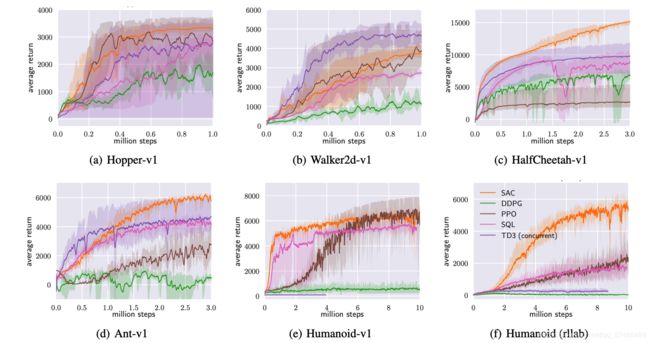
这篇论文引入了稳定的随机actor-critic形式，并使用off-policy方式更新参数，在一系列连续控制基准上达到state-of-the-art 结果，并且对不同的随机种子表现稳定。

引言

介绍一些论文引言中提到的关键点或强化学习中的知识点。

1. on-policy 与 off-policy：是对强化学习算法参数更新方式的划分。
   on-policy 要求每一次参数更新时，都需要同环境交互，采集新的经验样本来使用，也就是“边交互边学习”。当任务复杂时，需要的更新步骤和样本量激增，极大的增加了采样复杂度。
   off-policy 致力于重用过去的经验样本，特别是对Q-learning类的方法很适用。但是当off-policy和神经网络相结合时，对稳定性和收敛性造成了很大的挑战，特别是在连续的状态和动作空间。此类算法的典型代表是DDPG，采样复杂度低，优化能力强，但是收敛性非常脆弱且对超参数敏感。
2. actor-critic 实际上就是policy-iteration（策略迭代）方法的参数化，包含两个交替步骤：1）policy evaluation：估计策略的值函数(相当于critic)；2）policy improvement：根据值函数得到一个更优的新策略(相当于actor)。在复杂问题中，往往难以让某一个单独收敛，故采用联合优化方式。
3. 标准的强化学习最大化累积期望 reward ${\sum }_t{E}_{(s_t,a_t)\sim {\rho }_{\pi }}[r(s_t,a_t)]$
   最大熵强化学习的优化目标为：
   $$J(\pi )=\sum _{t=0}^T{E}_{(s_t,a_t)\sim {\rho }_{\pi }}[r(s_t,a_t)+\alpha H(\pi (\cdot |s_t))].$$超参数$\alpha$控制熵项的相对重要性，在后文推导中省略，因为等价于给 reward 项乘${\alpha }^{-1}$

这篇论文就是要讨论在连续的状态和动作空间如何设计有效且稳定的深度强化学习算法。
最大熵强化学习在标准的最大reward强化目标上增加了一个最大熵项，提高了探索能力和鲁棒性。
这篇文章提出的SAC，既降低了采样复杂度，又提高了收敛稳定性。SAC包含三个关键因素：
一个actor-critic结构，包括分离的策略网络和值函数网络，其中策略网络是一个随机actor；
一个off-policy更新方式，基于历史经验样本进行参数更新；
一个熵最大化目标，保证稳定性和探索能力。

理论推导：soft policy iteration

和actor-critic类似，soft actor-critic可以从一个最大熵版本的策略迭代中推导出来。

soft policy evaluation

$$T^{\pi }Q(s_t,a_t)\triangleq r(s_t,a_t)+\gamma E_{s_{t+1}\sim p}[V(s_{t+1})]$$其中，$T^{\pi }$是Bellman backup 算子，满足$Q^{k+1}=T^{\pi }{Q}^k$，且
$$V(s_t)=E_{a_t\sim \pi }[Q(s_t,a_t)-\log \pi (a_t|s_t)]$$引理1(soft 策略估计)：给定$T^{\pi }$和$Q^0$，则序列$Q^k(k\to \infty )$将会收敛至策略$\pi$的soft Q-value.

soft policy improvement

在策略改进中，我们有 ${\pi }_{new}(a_t|s_t)\propto \exp (Q^{{\pi }_{old}}(s_t,a_t))$
在实践中，为使策略易于处理，我们会将策略限制在一族策略集$\Pi$中，例如一族参数化的分布(如高斯分布)。为保证策略限制，我们必须将改进的策略投射进$\Pi$中。这篇论文采用信息投射，由KL散度定义，也就是说，在策略改进步骤，我们按照如下方式更新策略：
$${\pi }_{new}=\arg \underset{{\pi }^{\prime }\in \Pi }{\min }{D}_{KL}({\pi }^{\prime }(\cdot |s_t)\left|\right|\frac{\exp (Q^{{\pi }_{old}}(s_t,\cdot ))}{Z^{{\pi }_{old}}(s_t)})$$其中$Z^{{\pi }_{old}}(s_t)$是配分函数，与新策略梯度无关。
引理2(soft 策略改进)：对于任意$(s_t,a_t)\in S\times A,|A|<\infty$，有$Q^{{\pi }_{new}}(s_t,a_t)\ge Q^{{\pi }_{old}}(s_t,a_t)$

soft policy iteration

整个的soft 策略迭代交替使用以上两部分，并且会收敛至$\Pi$中的最优策略：
定理(soft 策略迭代)：从任意$\pi \in \Pi$开始，交替使用引理1和引理2，最终会收敛至策略${\pi }^{\ast }$，使得$Q^{{\pi }^{\ast }}(s_t,a_t)\ge Q^{\pi }(s_t,a_t),\forall \pi \in \Pi ,(s_t,a_t)\in S\times A,|A|<\infty$。其中 $|A|<\infty$是为了保证熵项有界。

模型：soft actor-critic

对于大规模连续控制问题，必须使用近似器对策略和Q-function进行近似，并使用SGD交替更新参数。我们考虑一个状态值函数$V_{\psi }(s_t)$，一个soft Q-function$Q_{\theta }(s_t,a_t)$，一个策略${\pi }_{\varphi }(a_t|s_t)$，参数分别为$\psi ,\theta ,\varphi$。其中值函数可被直接建模为神经网络，策略被建模为一个高斯分布，其均值向量和协方差矩阵都是由神经网络给出。
注意到，一般我们不估计状态值函数，因为它可以由Q-funciton和策略决定，但在实践中，增加这一项可以使得训练更稳定，同时也可以很方便地和其他网络共同训练。

训练状态值函数$V_{\psi }$

其中$a_t$是根据当前状态$s_t$生成的。

训练soft Q-function$Q_{\theta }$

更新中使用来target网络$\bar{\psi }$以切断相关性。

训练策略${\pi }_{\varphi }$

$$J_{\pi }(\varphi )=E_{s_t\sim D}\left[D_{KL}\right({\pi }_{\varphi }(\cdot |s_t)|\left|\frac{\exp (Q_{\theta }(s_t,\cdot ))}{Z_{\theta }(s_t)}\right)]$$我们利用神经网络重新参数化策略：
$$a_t=f_{\varphi }({ϵ}_t;s_t)$$其中${ϵ}_t$是一个从固定先验分布中采样的随机变量，如球形高斯分布。重写loss为：

算法

可以看作是DDPG的一个扩展版本

实验结果

最优性

稳定性

参数敏感性