编程之法:关于最长回文子串 | Manacher 算法详解
什么是最长回文子串呢?
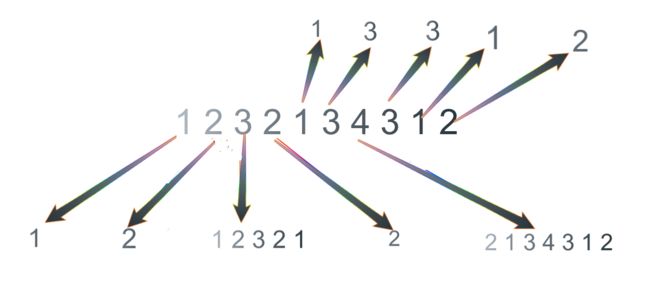
比如字符串:
1 2 3 2 1 3 4 3 1 2
其回文子串可以表示如下:
最大回文子串就是 4 对应的子串,子串长度为 7
转化为奇数长度
判断回文是要考虑是奇数还是偶数的,为了消除这个考虑,我们在字符串中添加 # 号:
abba ——— #a#b#b#a#
aba ———– #a#b#a#
这样,只考虑奇数情况就可以了
理解 O(n) 的 Manacher’s Algorithm
Manacher’s Algorithm,这个算法,本质上是非常非常简单的!要搞懂它在做什么
首先明确词汇:回文半径 ,就是整个回文的一半长度
我们在求最大的回文子串的时候,就是遍历 从0到n-1的 位置的,计算出每一位作为回文中间的对应回文长度,然后取最大的那一个。
举例:
# a # b # a # a # b #
其中每一位对应的 回文半径 长度为:
1 2 1 4 1 2 5 2 1 2 1
比如 : 第二个位置对应的回文是 # a #,一半是 a #,所以长度就是 2。
Manacher算法还是遍历每一个位置,求出所有位置对应的回文半径长度,然后取最大值。这个算法中主要做的内容在于:
如何利用已知的信息,优化求 当前位置 对应的 回文半径长度
我们一步一步的来看:
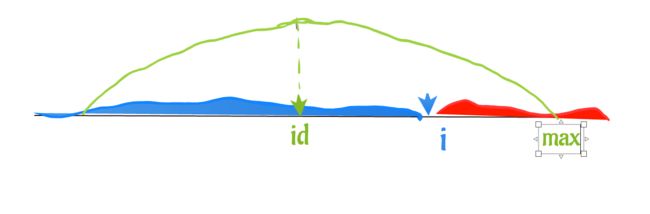
黑色线段想象为整个字符串
i 为当前需要计算 回文半径 的位置
我们可以知道,i之前对应的位置,回文半径都是已知的,而 i 之后对应的位置,回文半径都是未知的,如图:
在已知区域内,每一个 位置 都对应一个 最右边,最右边是以这个位置为中间的回文子串,的最右边位置
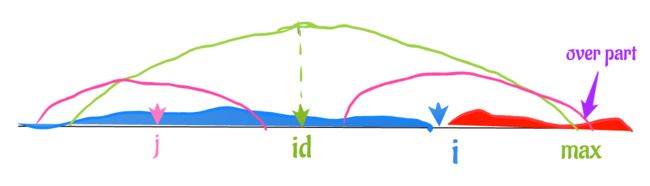
如下图,我们假设可以看到 i 之前的两个位置 a,b 分别对应的最右边为 max_a,max_b:
我们找出前面所有位置中,max最大的那一个,此图中显示的max是前面所有点中可以到达的最大max
我们用 id 来标记这个 max 对应的 位置
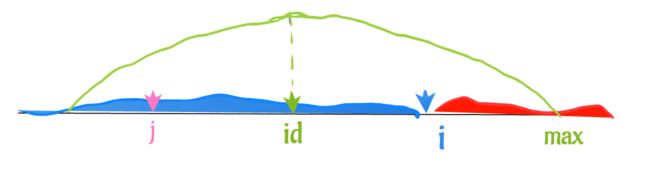
然后我们来求 i 关于 id 的对称位置,用 j 标记 (这个对称位置很重要!!对称,就是 id -j = i-id)
我们现在有 i,id,max,j四个值
我们还用 p[i], p[j], p[id] 来表示这些位置对应的 回文半径长度(在程序中,我们使用一个数组来存储这些位置的 回文半径长度)
因为 j,id,都在已知部分,所以,p[j],p[id]都是已知的。
在图中,绿色范围就是 id为中间的回文子串范围,max-id就是半径
现在我们根据这些信息来求 p[i],然后更新信息就可以求 p[i+1],p[i+2] 等等…
得知这些信息会如何优化呢?
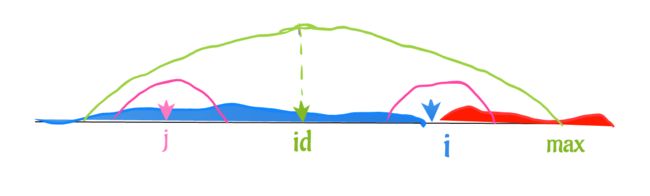
可能大家已经想到了,既然 i,j是关于id对称的,那么 p[i] 肯定和 p[j] 有联系。
当 p[j] < max - i 的时候,如下图:
因为 i,j 是对称相等关系,所以j覆盖的部分,i必然是覆盖到的,必然 p[i] 的大小,绝对不会小于 p[j]
所以计算 p[i] 时,我们可以从 p[i] = p[j] 起步
而另一种情况是 p[j] 大于 max-i,如下图(over part 既指 超出的部分):
一目了然,在max-i的范围内,i 和 j还是关于id对称的,我们可以保证相等,但是在超出部分,没法保证相等,所以此时只能说 p[i] 不小于 max-i
我们在计算 p[i] 的时候,可以从 max-i 开始
不过,如果max都没有大于i,也就是 max 在 i 的左边,那就不用折腾了,老老实实 p[i] = 1 开始计算吧!
这就是计算 以i为中间的回文子串半径的全部步骤了
上面写了每次计算完要 更新信息,就是要更新 max 和 id,i 的 p[i] 所指的位置可能比max还要大,成为新的 max,那么 i 也就是新的 id 了
再去看核心代码是不是很好懂了?
for (i = 0; i < len; i++){
if (maxid > i){
p[i] = min(p[2*id - i], maxid - i); // j = 2*id-i (对称是这么计算的)
}
else{
p[i] = 1;
}
while (newstr[i+p[i]] == newstr[i-p[i]])
p[i]++;
if (p[i] + i > maxid){
maxid = p[i] + i;
id = i;
}
if (ans < p[i])
ans = p[i];
}
最后推荐两个相关博客文章,我在学习过程中有借鉴:
博客1
博客2