python计算矩阵间的欧式距离

背景：计算一个M*D的二维矩阵与一个N*D的二维矩阵各个行向量之间的距离，不用循环来做。

• 如果计算两个一维向量P，C的维数相同，则它们的欧氏距离为
  
  • 化简之后为
    
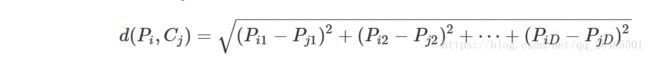
• 我们继而推广，一个一维向量与一个二维矩阵各个行向量的欧氏距离为：
  
• 再继续推广到一个二维矩阵M个行向量与另一个矩阵N个行向量的欧式距离形成的一个二维矩阵矩阵为M*N：
  

最终结果为三个M*N的二维矩阵求和：
1. 第一个矩阵为P的各行向量模长平方的矩阵，如下

⎛⎝⎜⎜⎜⎜⎜||p1||2||p2||2⋮||pM||2||p1||2||p2||2⋮||pM||2⋯⋯⋯⋯||p1||2||p2||2⋮||pM||2⎞⎠⎟⎟⎟⎟⎟ ( | | p 1 | | 2 | | p 1 | | 2 ⋯ | | p 1 | | 2 | | p 2 | | 2 | | p 2 | | 2 ⋯ | | p 2 | | 2 ⋮ ⋮ ⋯ ⋮ | | p M | | 2 | | p M | | 2 ⋯ | | p M | | 2 )

2. 第二个矩阵为C的矩阵的各个行向量的模长平方的矩阵，如下：

⎛⎝⎜⎜⎜⎜⎜||C1||2||C1||2⋮||C1||2||C2||2||C2||2⋮||C2||2⋯⋯⋯⋯||Cn||2||Cn||2⋮||Cn||2⎞⎠⎟⎟⎟⎟⎟ ( | | C 1 | | 2 | | C 2 | | 2 ⋯ | | C n | | 2 | | C 1 | | 2 | | C 2 | | 2 ⋯ | | C n | | 2 ⋮ ⋮ ⋯ ⋮ | | C 1 | | 2 | | C 2 | | 2 ⋯ | | C n | | 2 )

3. 第三个矩阵为P与C转置的数乘运算为：2*P*C’

最后将三个矩阵加起来，求开方，结果就是矩阵间欧式距离的计算公式。

引用参考：

https://blog.csdn.net/zhyh1435589631/article/details/54236643