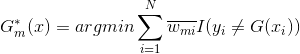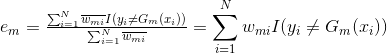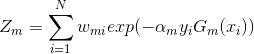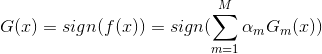《统计学习方法》-李航、《机器学习-西瓜书》-周志华总结+Python代码连载(五)--集成学习_提升方法
一、集成学习概论
集成学习(Ensemble learning)通过构建并结合多个学习器来完成学习任务,实际上,就是“三个臭皮匠顶个诸葛亮”的道理。
集成学习通过将多个学习器进行结合,常可获得比单一学习器显著优越的泛化能力。这对“弱学习器(weak learner)”尤为明显,因此集成学习的很多理论研究都是针对弱学习器进行的,而基学习器有时也被称为弱学习器。
一般根据弱学习器有无依赖关系,大体分为两个流派Boosting和Bagging
a.Boosting:弱学习器之间有依赖关系,常见的算法有Adaboost,GBDT,Xgboost。
b.Bagging:弱学习器之间无依赖关系,常见的算法有随机森林(RandomForest)。
二、提升树模型
以决策树为基函数的提升方法称为提升树(boosting-tree),对于分类问题决策树是二叉分类树,对回归问题的是二叉回归树。
2.1 提升树模型可以表示为决策树的加法模型:
![]() 表示决策树;
表示决策树;![]() 为决策树的参数;M为树的个数。
为决策树的参数;M为树的个数。
2.2 提升树算法
提升树算法采用前向分布算法,首先明确初始提升树![]() =0,第m步的模型是
=0,第m步的模型是![]() 。
。
针对不同问题的提升树的算法,主要区别在于使用的损失函数不同,有用指数损失函数的分类问题(三节会讲),这里主要是用平方误差的回归问题。
已知一个训练集![]() ,通过回归树的性质,将输出空间划分为J个互不相交的区域
,通过回归树的性质,将输出空间划分为J个互不相交的区域![]() ,并且在每个区域上确定输出的常量
,并且在每个区域上确定输出的常量![]() ,那么树可表示为:
,那么树可表示为:
参数![]() 表示树的区域划分和各个区域上的常数,J是回归树的复杂度即叶结点个数。
表示树的区域划分和各个区域上的常数,J是回归树的复杂度即叶结点个数。
当采用平方误差时,![]() ,于是损失变为
,于是损失变为 ![]()
其中r为残差,所以对于回归问题的提升树算法来说,只需要简单的拟合当前模型的残差,总结回归问题的提升树算法:
step1.初始化![]() 。
。
step2.对m=1,...,M
a.计算残差 ![]() ,N为样本数。
,N为样本数。
b.拟合残差学习一个回归树![]() 。
。
c.更新![]()
step3.得到回归问题的提升树
三、AdaBoost模型
该模型主要是使用指数损失函数的分类问题,L(x,f(x)) = exp[-yf(x)],
假设经过m-1次迭代得到![]() ,在m次迭代有
,在m次迭代有![]() ,其中
,其中![]() 是拟合指数损失函数最下而得到的,即:
是拟合指数损失函数最下而得到的,即:
其中![]() ,既不依赖
,既不依赖![]() 也不依赖G,所以与最小化无关,但依赖于
也不依赖G,所以与最小化无关,但依赖于![]() ,每一次迭代而发生改变。
,每一次迭代而发生改变。
下面求解![]() :
:
将求解的
![]() 带入,对
带入,对![]() 求导使导数等于0,可得到:
求导使导数等于0,可得到:
总结Adaboost算法:
step2.对m=1,2,...,m
a.使用权值![]() 的训练集学习,得到基本分类器。
的训练集学习,得到基本分类器。
b.计算![]() 在训练集上的分类误差率
在训练集上的分类误差率
c.计算![]() 的系数
的系数
d.更新训练数据集的权值分布
![]()
![]()
step3.得到最终分类器
代码实现:
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i,-1] == 0:
data[i,-1] = -1
# print(data)
return data[:,:2], data[:,-1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()
#adaboost in python
class AdaBoost:
def __init__(self, n_estimators=50, learning_rate=1.0):
self.clf_num = n_estimators
self.learning_rate = learning_rate
def init_args(self, datasets, labels):
self.X = datasets
self.Y = labels
self.M, self.N = datasets.shape
# 弱分类器数目和集合
self.clf_sets = []
# 初始化weights
self.weights = [1.0 / self.M] * self.M
# G(x)系数 alpha
self.alpha = []
def _G(self, features, labels, weights):
m = len(features)
error = 100000.0 # 无穷大
best_v = 0.0
# 单维features
features_min = min(features)
features_max = max(features)
n_step = (features_max - features_min +
self.learning_rate) // self.learning_rate
direct, compare_array = None, None
for i in range(1, int(n_step)):
v = features_min + self.learning_rate * i
if v not in features:
# 误分类计算
compare_array_positive = np.array(
[1 if features[k] > v else -1 for k in range(m)])
weight_error_positive = sum([
weights[k] for k in range(m)
if compare_array_positive[k] != labels[k]
])
compare_array_nagetive = np.array(
[-1 if features[k] > v else 1 for k in range(m)])
weight_error_nagetive = sum([
weights[k] for k in range(m)
if compare_array_nagetive[k] != labels[k]
])
if weight_error_positive < weight_error_nagetive:
weight_error = weight_error_positive
_compare_array = compare_array_positive
direct = 'positive'
else:
weight_error = weight_error_nagetive
_compare_array = compare_array_nagetive
direct = 'nagetive'
# print('v:{} error:{}'.format(v, weight_error))
if weight_error < error:
error = weight_error
compare_array = _compare_array
best_v = v
return best_v, direct, error, compare_array
# 计算alpha
def _alpha(self, error):
return 0.5 * np.log((1 - error) / error)
# 规范化因子
def _Z(self, weights, a, clf):
return sum([
weights[i] * np.exp(-1 * a * self.Y[i] * clf[i])
for i in range(self.M)
])
# 权值更新
def _w(self, a, clf, Z):
for i in range(self.M):
self.weights[i] = self.weights[i] * np.exp(
-1 * a * self.Y[i] * clf[i]) / Z
# G(x)的线性组合
def _f(self, alpha, clf_sets):
pass
def G(self, x, v, direct):
if direct == 'positive':
return 1 if x > v else -1
else:
return -1 if x > v else 1
def fit(self, X, y):
self.init_args(X, y)
for epoch in range(self.clf_num):
best_clf_error, best_v, clf_result = 100000, None, None
# 根据特征维度, 选择误差最小的
for j in range(self.N):
features = self.X[:, j]
# 分类阈值,分类误差,分类结果
v, direct, error, compare_array = self._G(
features, self.Y, self.weights)
if error < best_clf_error:
best_clf_error = error
best_v = v
final_direct = direct
clf_result = compare_array
axis = j
if best_clf_error == 0:
break
# 计算G(x)系数a
a = self._alpha(best_clf_error)
self.alpha.append(a)
# 记录分类器
self.clf_sets.append((axis, best_v, final_direct))
# 规范化因子
Z = self._Z(self.weights, a, clf_result)
# 权值更新
self._w(a, clf_result, Z)
def predict(self, feature):
result = 0.0
for i in range(len(self.clf_sets)):
axis, clf_v, direct = self.clf_sets[i]
f_input = feature[axis]
result += self.alpha[i] * self.G(f_input, clf_v, direct)
# sign
return 1 if result > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
feature = X_test[i]
if self.predict(feature) == y_test[i]:
right_count += 1
return right_count / len(X_test)
X = np.arange(10).reshape(10, 1)
y = np.array([1, 1, 1, -1, -1, -1, 1, 1, 1, -1])
clf = AdaBoost(n_estimators=3, learning_rate=0.5)
clf.fit(X, y)
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
clf = AdaBoost(n_estimators=10, learning_rate=0.2)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
# 100次结果
result = []
for i in range(1, 101):
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
clf = AdaBoost(n_estimators=100, learning_rate=0.2)
clf.fit(X_train, y_train)
r = clf.score(X_test, y_test)
result.append(r)
print('average score:{:.3f}%'.format(sum(result)))
#adaboost in sklearn
from sklearn.ensemble import AdaBoostClassifier
clf = AdaBoostClassifier(n_estimators=100, learning_rate=0.5)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)连载GitHub同步更新:https://github.com/wenhan123/ML-Python-
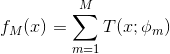

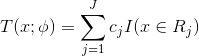
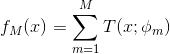
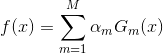
![(\alpha _m,G_m(x)) = argmin_{\alpha ,G} \sum_{i=1}^N exp[-y_i(f_{m-1(x_i)+\alpha G(x_i)})] = argmin_{\alpha ,G} \sum_{i=1}^N\overline{w_{mi}}exp[-y_i\alpha G(x_i)]](http://img.e-com-net.com/image/info8/02d888631b1e417880b59918b65fdc4d.gif)