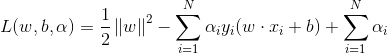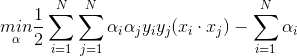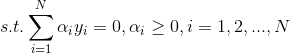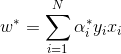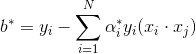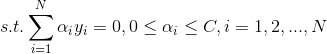机器学习实战之SVM
SVM比较难，涉及到很多复杂的算法和公式推导，暂时没有完全吃透，本文仅作为自己初学笔记，可能会有疏漏和错误。
1.线性可分支持向量机
给定一堆线性可分的数据点X，它们属于两类（y=1或-1），SVM学习的目标是找到一个超平面，将特征空间划分为两部分，一部分为正类，一部分为负类。超平面方程表示为
（1）
相应的分类决策函数
（2）
2.函数间隔与几何间隔
将数据点分开的超平面可能有很多个，怎样选择最合适的超平面呢，这里要引入间隔的 概念。
一般来说，一个点距离分离超平面的远近可以表示分类预测的确信程度，在超平面一定的情况下，
能够相对表示点x距离超平面的远近，而
与类标记y的符号是否一致能够表示分类是否正确。所以用
来表示分类的正确性及确信度。
定义超平面关于样本点
的函数间隔为：
（3）
定义超平面关于数据集T的函数间隔为超平面关于所有数据点的函数间隔最小值
（4）
成比例地改变w和b，超平面不变呢，但是函数间隔会随之改变，于是我们对函数间隔进行规范化
定义超平面关于样本点的几何间隔为：
（5）
定义超平面关于数据集T的几何间隔为超平面关于所有数据点的几何间隔最小值
（6）
SVM的目标就是找到几何间隔最大的超平面，可以表示为以下约束问题：
（7）
（8）
考虑到函数间隔与几何间隔的关系，并取
，得到最优化问题：
（9）
（10）
这是一个凸二次规划问题。求得最优解
即可得到分离超平面。
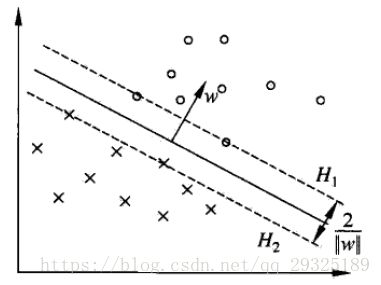
3.支持向量和间隔边界
在线性可分情况下，训练数据集样本点中与分离超平面距离最近的样本点的实例称为支持向量（support vector）。支持向量是使约束条件（10）等号成立的点。即
,如图在H1和H2上的点就是支持向量。
H1 和H2之间的距离称为间隔（margin），间隔依赖于分离超平面的法向量，等于
，H1和H2称为间隔边界。
4.学习的对偶算法
为了求解上述最优化问题，应用拉格朗日对偶性原理，通过求解对偶性问题来求解。
首先构建拉格朗日函数，对每一个不等式函数引入拉格朗日乘子
,定义拉格朗日函数
(11)
得到等价约束问题：
(12)
(13)
求得最优解
计算 
(14)
并选择
一个正分量
,计算
(15)
5.线性不可分问题
线性不可分意味着某些样本点不能满足函数间隔大于1的约束条件（10），为了解决这个问题可以对每一个样本点引入一个松弛变量
,这样约束问题变为
,
同时对每一个松弛变量，支付一个代价，目标函数变为
（16）
C 称为惩罚参数，C值大时对误分类惩罚增加，C值小时对误分类惩罚减小
对应对偶问题为：
（17）
（18）
6.核函数
在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。如图所示，一堆数据在二维空间无法划分，从而映射到三维空间里划分：
设存在一个映射，
将输入空间映射到一个高维特征空间，函数K（x,z）满足条件
则称K(x,z)为核函数，为映射函数，
为和
的内积。
核函数方法的优点是只需要定义核函数，不需要显式定义映射函数，也不需要构造映射后的多维空间。
在SVM中的应用，将
与x_{j}的内积换为
,即目标函数（17）变为：
相应分类决策函数中内积也换为核函数
- 多项式核，显然刚才我们举的例子是这里多项式核的一个特例（R = 1，d = 2）。虽然比较麻烦，而且没有必要，不过这个核所对应的映射实际上是可以写出来的，该空间的维度是
，其中 m 是原始空间的维度。 - 高斯核
，这个核就是最开始提到过的会将原始空间映射为无穷维空间的那个家伙。不过，如果
选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间：
- 线性核
，这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了(意思是说，咱们有的时候，写代码，或写公式的时候，只要写个模板或通用表达式，然后再代入不同的核，便可以了，于此，便在形式上统一了起来，不用再分别写一个线性的，和一个非线性的)。
7.序列最小最优化算法（SMO）
SMO算法是求解（12）凸二次对偶问题的算法。具体步骤参见https://blog.csdn.net/v_july_v/article/details/7624837
实例代码：
from numpy import *
def loadData(filename):
fr=open(filename)
dataMat=[]
dataLabel=[]
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
dataLabel.append(float(lineArr[2]))
return dataMat,dataLabel
#随机选择j，j!=i
def selectJrand(i,m):
j=i
while(j==i):
j=int(random.uniform(1,m))
return j
#对alpha进行修剪
def clipAlpha(aj,H,L):
if aj>H:
return H
if ajtoler and alpha[i]>0):
j=selectJrand(i,m) #如果找到了alpha1，则随机挑选alpha2
fXj=float(multiply(alpha,datalabel).T*(dataMatrix*dataMatrix[j,:].T))+b
Ej=fXj-float(datalabel[j])
alphaIold=alpha[i].copy()
alphaJold=alpha[j].copy()
if datalabel[i]==datalabel[j]:
L=max(0,alpha[j]+alpha[i]-C)
H=min(C,alpha[j]+alpha[i])
else:
L=max(0,alpha[j]-alpha[i])
H=min(C,C+alpha[j]-alpha[i])
if L==H:
#print('L=H')
continue
#eta=+-2
eta = -2.0 * dataMatrix[i, :] * dataMatrix[j, :].T +dataMatrix[i, :] * dataMatrix[i, :].T + dataMatrix[j,:]*dataMatrix[j,:].T
if eta<=0:
#print('eta<=0')
continue
alpha[j]+=datalabel[j]*(Ei-Ej)/eta
alpha[j]=clipAlpha(alpha[j],H,L)
if (abs(alpha[j]-alphaJold)<0.00001):
#print('J not moving enough')
continue
#alpha2变化足够大时选中
#更新alpha1
alpha[i]=alphaIold+datalabel[i]*datalabel[j]*(alphaJold-alpha[j])
#更新b
b1 = b - Ei- datalabel[i]*(alpha[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - datalabel[j]*\
(alpha[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej- datalabel[i]*(alpha[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - datalabel[j]*\
(alpha[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alpha[i]) and (C > alpha[i]):
b = b1
elif (0 < alpha[j]) and (C > alpha[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
#print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
if alphaPairsChanged==0:
iter+=1
#print( "iteration number: %d" % iter)
return alpha,b
def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
m,n = shape(X)
K = mat(zeros((m,1)))
if kTup[0]=='lin': K = X * A.T #linear kernel
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
else: raise NameError('Houston We Have a Problem -- \
That Kernel is not recognized')
return K
#完整版Platt SMO
#定义一个优化的结构
class optStruct:
def __init__(self,dataMat,labelMat,C,toler,kTup):
self.X=dataMat
self.dataMat=dataMat
self.labelMat=labelMat
self.C=C
self.tol=toler
self.m=shape(dataMat)[0]
self.alpha=mat(zeros((self.m,1)))
self.b=0
self.eCache=mat(zeros((self.m,2)))#误差缓存，m*2的矩阵，第一列为E值是否有效的标志位，第二列为E值
self.K = mat(zeros((self.m, self.m)))
for i in range(self.m):
self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)
#计算Ek
def calcEk(oS, k):
fXk = float(multiply(oS.alpha, oS.labelMat).T * (oS.X*oS.X[k,:].T) + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
#选择内循环j
def selectJ(i,oS,Ei):
maxK=-1
maxDeltaE=0
Ej=0
oS.eCache[i]=[1,Ei]
validEcacheList=nonzero(oS.eCache[:,0].A)[0] #返回有效的E值索引
if len(validEcacheList)>1:
for k in validEcacheList:
if k==i:
continue
Ek=calcEk(oS,k)
deltaE=abs(Ei-Ek)
if deltaE>maxDeltaE:
maxK=k
deltaE=maxDeltaE
Ej=Ek
return maxK,Ej
else:
j = selectJrand(i, oS.m)
Ej = calcEk(oS, j)
return j, Ej
#更新Ek，每次更新alpha后都要重新计算Ek
def updateEk(oS,k):
Ek=calcEk(oS,k)
oS.eCache[k]=[1,Ek]
#外循环
def innerL(i, oS):
Ei = calcEk(oS, i)
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alpha[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alpha[i] > 0)):
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
alphaIold = oS.alpha[i].copy(); alphaJold = oS.alpha[j].copy();
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alpha[j] - oS.alpha[i])
H = min(oS.C, oS.C + oS.alpha[j] - oS.alpha[i])
else:
L = max(0, oS.alpha[j] + oS.alpha[i] - oS.C)
H = min(oS.C, oS.alpha[j] + oS.alpha[i])
if L==H:
#print ("L==H")
return 0
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
#eta = 2.0 * oS.dataMat[i, :] * oS.dataMat[j, :].T - oS.dataMat[i, :] * oS.dataMat[i, :].T - oS.dataMat[j,:] * oS.dataMat[j, :].T
if eta >= 0:
#print ("eta>=0")
return 0
oS.alpha[j] -= oS.labelMat[j]*(Ei - Ej)/eta
oS.alpha[j] = clipAlpha(oS.alpha[j],H,L)
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alpha[j] - alphaJold) < 0.00001):
#print ("j not moving enough")
return 0
oS.alpha[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alpha[j])#update i by the same amount as j
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
b1 = oS.b - Ei- oS.labelMat[i]*(oS.alpha[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alpha[j]-alphaJold)*oS.K[i,j]
b2 = oS.b - Ej- oS.labelMat[i]*(oS.alpha[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alpha[j]-alphaJold)*oS.K[j,j]
if (0 < oS.alpha[i]) and (oS.C > oS.alpha[i]): oS.b = b1
elif (0 < oS.alpha[j]) and (oS.C > oS.alpha[j]): oS.b = b2
else: oS.b = (b1 + b2)/2.0
return 1
else: return 0
#完整版SMO
def smoP(dataMat,labelMat,C,toler,maxIter,kTup=('lin',0)):
oS = optStruct(mat(dataMat), mat(labelMat).transpose(), C, toler,kTup)
iter = 0
entireSet = True
alphaPairsChanged = 0
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
if entireSet: # go over all
for i in range(oS.m):
alphaPairsChanged += innerL(i, oS)
#print("fullSet, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
else: # go over non-bound (railed) alpha
nonBoundIs = nonzero((oS.alpha.A > 0) * (oS.alpha.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i, oS)
#print("non-bound, iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))
iter += 1
if entireSet:
entireSet = False # toggle entire set loop
elif (alphaPairsChanged == 0):
entireSet = True
#print("iteration number: %d" % iter)
return oS.b, oS.alpha
#计算W，求得分离超平面
def calcWs(alphas,dataArr,classLabels):
X = mat(dataArr); labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i],X[i,:].T)
return w
#径向基核函数 测试
def testRbf(k1=1.3):
dataArr,labelArr = loadData('D:\python\code\machinelearninginaction\Ch06\\testSetRBF.txt')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd] #get matrix of only support vectors
labelSV = labelMat[svInd];
print ("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadData('D:\python\code\machinelearninginaction\Ch06\\testSetRBF2.txt')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the test error rate is: %f" % (float(errorCount)/m))
#testRbf(0.2)
# 基于SVM 的手写数字识别
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def loadImages(dirName):
from os import listdir
hwLabels = []
trainingFileList = listdir(dirName) #load the training set
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
if classNumStr == 9: hwLabels.append(-1)
else: hwLabels.append(1)
trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
return trainingMat, hwLabels
def testDigits(kTup=('lin', 10)):
dataArr,labelArr = loadImages('D:\python\code\machinelearninginaction\Ch06\digits\\trainingDigits')
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
svInd=nonzero(alphas.A>0)[0]
sVs=datMat[svInd]
labelSV = labelMat[svInd]
print ("there are %d Support Vectors" % shape(sVs)[0])
m,n = shape(datMat)
errorCount = 0
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the training error rate is: %f" % (float(errorCount)/m))
dataArr,labelArr = loadImages('D:\python\code\machinelearninginaction\Ch06\digits\\testDigits')
errorCount = 0
datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
m,n = shape(datMat)
for i in range(m):
kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
if sign(predict)!=sign(labelArr[i]): errorCount += 1
print ("the test error rate is: %f" % (float(errorCount)/m))