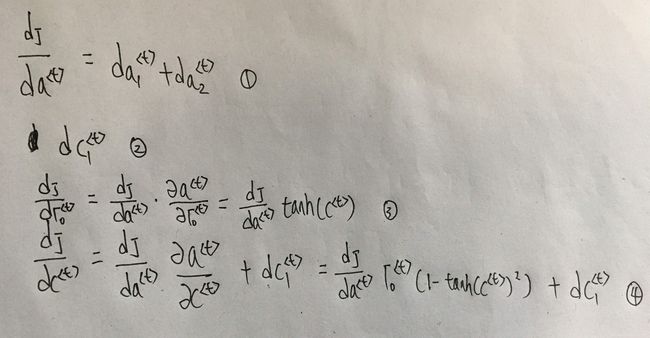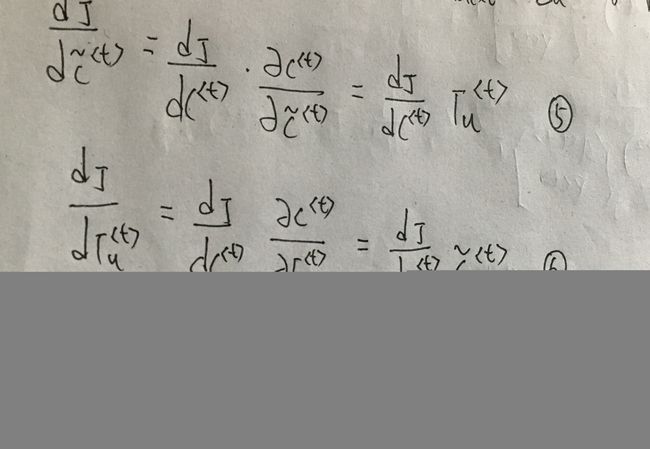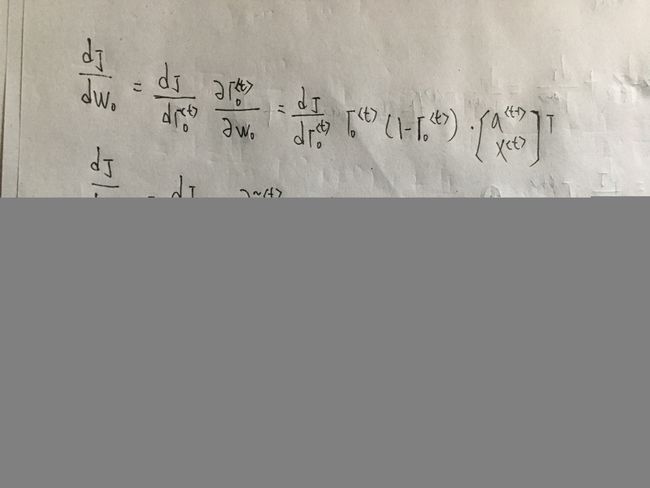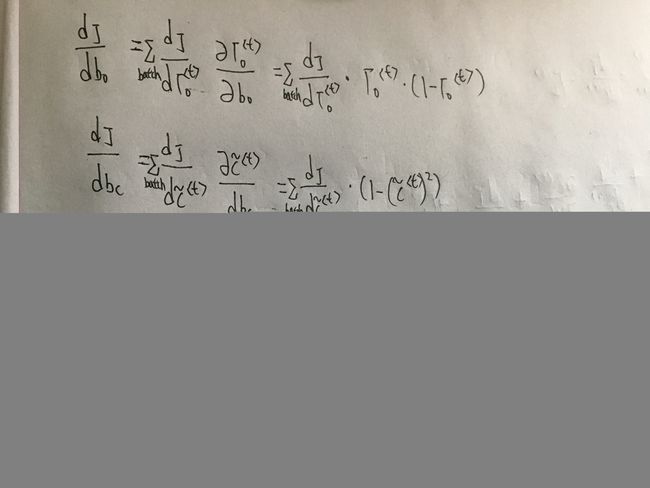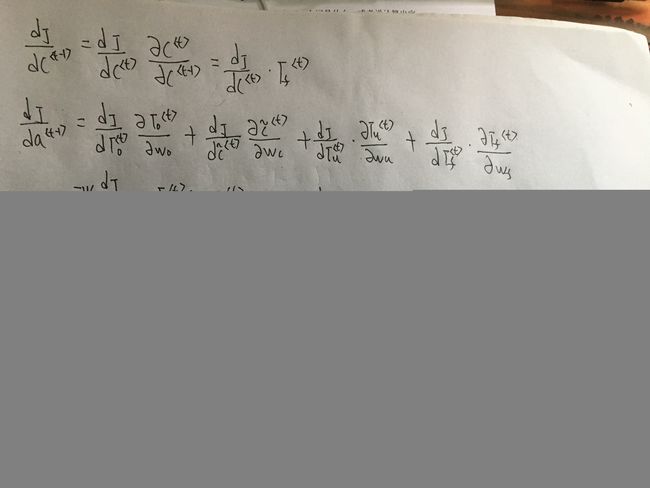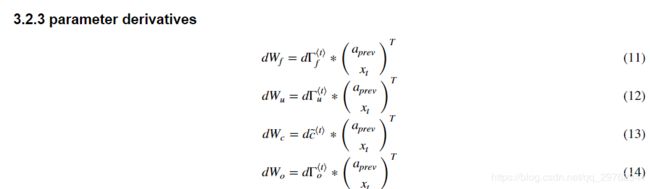RNN、LSTM反向传播推导详解

在做吴恩达深度学习课程相关作业时，顺便进行了RNN和LSTM的反向传播推导。顺便记录如下，希望能对你有所帮助~

RNN前向与反向:

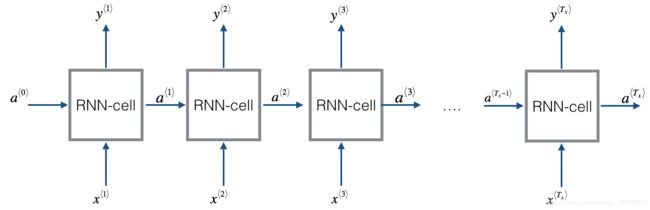
模型的整体结构如下图所示，输入的是序列x、输出y，长度为Tx。

 

BasicRNN 前向传播

 现在我们单独对每个cell进行公式推导，最终整个模型的公式其实就是单个cell的循环调用。

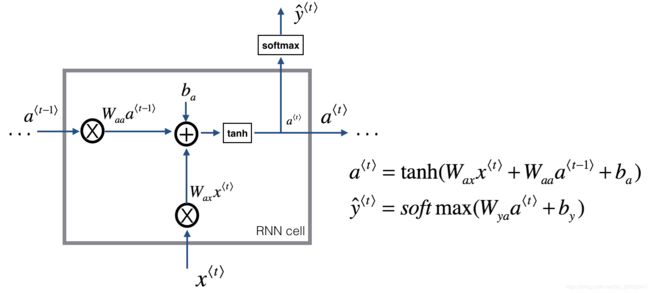
 下图是单个cell的具体结构图，以及前向传播的公式，非常的简洁明了 

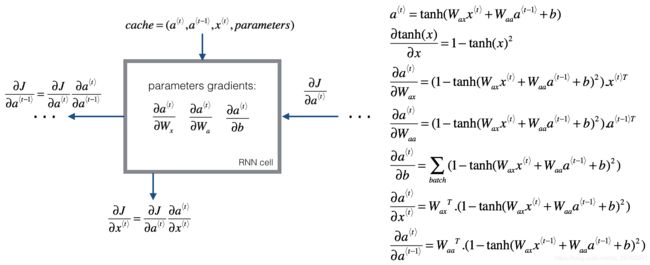
Basic RNN的反向传播很简单，直接上图:

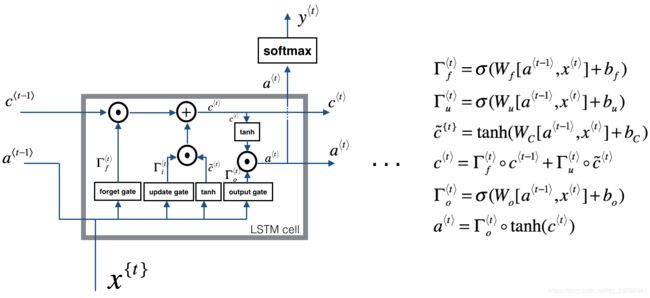
LSTM前向传播

 

LSTM单个cell的反向传播比Basic RNN看起来要复杂很多，主要变化就是添加了三个门：遗忘门、更新门和输出门。但是我们理清楚单个cell接收到的所有梯度，就很容易理解了。 
（1）当前cell中a< t >通过反向传播得到的梯度同样有两个部分 
    - 当前输出y^< t >代入损失函数，对a< t >求导得到的da< t >1 
    - 输入到下一个cell的a< t >传回的梯度da< t >2 
（2）当前cell还要接受输入到下一个cell的c< t >传回的梯度dc< t >1

 

为了便于理解，现在图上标记一些符号：

注意其中的 da 是同 da1与da2 反向来的，而 dc 是由 dc1与da 反向来的

LSTM反向传播详细推导(第一种推导法)

PS：这里是本人根据吴恩达作业结合自己理解推导出来的。之所以自己宁愿手撕推导一遍，再（二）中讲明原因。

第一步计算反向传播:

第二步计算反向传播:

第三步计算反向传播:

第四步计算反向传播:

 

第五步计算反向传播:

注意第五步这里的 W前 W 后要分别对应 a 和 x 的维数。

至此，整个LSTM反向传播完成~~~

LSTM反向传播详细推导(第二种推导法)

PS： 之所以手推了上面的(一）。是因为一开始看吴恩达作业列的式子时，有些不明白式子怎么会这样，例如dot = da_next * np.tanh(c_next) * ot * (1 - ot)，但是后来结合了代码去看，发现ot * (1 - ot)是把应该在后面才求导的式子中部分计算直接在前面给计算了，例如dwf的求导，这里就不用ot * (1 - ot)。。。当然这样结果是对的，只是一开始真把我搞糊涂了。（这里的dc并没有像上面那样直接单独算出整体结果）

注意：  图中标记的1部分是计算dWo时才用到的，但是下面的dWo没列出，这里提前列出来了。。。(8)(9)(10)后面的下划线部分都是一样提前计算了，真正的反向求导只是中扩号里面的。一开始觉得很奇怪，后来结合整体结合才看明白了。至于为什么提前计算，就是为了后面的公式写起来简单吧~

          （8）式中画叉的应该是图错了，把那个去掉。

实现代码如下:

def lstm_cell_backward(da_next, dc_next, cache):
    """
    Implement the backward pass for the LSTM-cell (single time-step).

    Arguments:
    da_next -- Gradients of next hidden state, of shape (n_a, m)
    dc_next -- Gradients of next cell state, of shape (n_a, m)
    cache -- cache storing information from the forward pass

    Returns:
    gradients -- python dictionary containing:
                        dxt -- Gradient of input data at time-step t, of shape (n_x, m)
                        da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m)
                        dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x)
                        dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x)
                        dWi -- Gradient w.r.t. the weight matrix of the input gate, numpy array of shape (n_a, n_a + n_x)
                        dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x)
                        dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x)
                        dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1)
                        dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1)
                        dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1)
                        dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1)
    """

    # Retrieve information from "cache"
    (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache
    
    ### START CODE HERE ###
    # Retrieve dimensions from xt's and a_next's shape (≈2 lines)
    n_x, m = xt.shape
    n_a, m = a_next.shape
    
    # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines)
    dot = da_next * np.tanh(c_next) * ot * (1 - ot)
    dcct = (dc_next * it + ot * (1 - np.square(np.tanh(c_next))) * it * da_next) * (1 - np.square(cct))
    dit = (dc_next * cct + ot * (1 - np.square(np.tanh(c_next))) * cct * da_next) * it * (1 - it)
    dft = (dc_next * c_prev + ot *(1 - np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1 - ft)
 

    # Compute parameters related derivatives. Use equations (11)-(14) (≈8 lines)
    dWf = np.dot(dft,np.concatenate((a_prev, xt), axis=0).T)
    dWi = np.dot(dit,np.concatenate((a_prev, xt), axis=0).T)
    dWc = np.dot(dcct,np.concatenate((a_prev, xt), axis=0).T)
    dWo = np.dot(dot,np.concatenate((a_prev, xt), axis=0).T)
    dbf = np.sum(dft, axis=1 ,keepdims = True)
    dbi = np.sum(dit, axis=1, keepdims = True)
    dbc = np.sum(dcct, axis=1,  keepdims = True)
    dbo = np.sum(dot, axis=1, keepdims = True)

    # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (15)-(17). (≈3 lines)
    da_prev = np.dot(parameters['Wf'][:,:n_a].T,dft)+np.dot(parameters['Wi'][:,:n_a].T,dit)+np.dot(parameters['Wc'][:,:n_a].T,dcct)+np.dot(parameters['Wo'][:,:n_a].T,dot)
    dc_prev = dc_next*ft+ot*(1-np.square(np.tanh(c_next)))*ft*da_next
    dxt = np.dot(parameters['Wf'][:,n_a:].T,dft)+np.dot(parameters['Wi'][:,n_a:].T,dit)+np.dot(parameters['Wc'][:,n_a:].T,dcct)+np.dot(parameters['Wo'][:,n_a:].T,dot)
    # parameters['Wf'][:, :n_a].T 每一行的 第 0 到 n_a-1 列的数据取出来
    # parameters['Wf'][:, n_a:].T 每一行的 第 n_a 到最后列的数据取出来
    ### END CODE HERE ###
    
    # Save gradients in dictionary
    gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi,
                "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo}

    return gradients