算法——二分查找与其他
算法——二分查找
- 二分查找
- 简介
- 查找前提
- 原理
- 代码实现
- 注意
- 类似的查找方法
- 复杂度分析
二分查找
简介
二分查找(Binary Search)又被称为折半查找,它是一种效率较高[1]的查找方法。
查找前提
源数据是有序的——数列有序,数列使用顺序储存储存结构(例如 数组 )。
原理
二分查找不断地通过比较和取中值来缩小区间的左右边界,直到命中预期数据。
注意: 对命中数据需要分清键值对,在调整区间时,调整的是键,而进行数据比较的时候,比较的是值。
代码实现
- 算法(第四版)使用代码
static void Main(string[] args)
{
int[] arrayM = new int[15] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 };
int[] arrayL = new int[5] { 1,16,4,0,7 };
foreach (int key in arrayL)
{
int outputIndex = BinarySearch(arrayM, key);
if (outputIndex >= 0) Console.WriteLine(arrayM[outputIndex]+" is in the arrayM.");
}
Console.Read();
}
static int BinarySearch(int[] inputArray, int key)
{
int left = 0;
int right = inputArray.Length-1;
while (left <= right)
{
int mid = (left + right) / 2;
if (inputArray[mid] > key) right = mid - 1;
else if (inputArray[mid] < key) left = mid + 1;
else return mid;
}
return -1;
}
- 使用递归的二分查找
static void Main(string[] args)
{
int[] arrayM = new int[15] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 };
int[] arrayL = new int[5] { 1, 16, 4, 0, 7 };
foreach (int value in arrayL)
{
int outputIndex = BinarySearchRecursion(arrayM, value, 0, arrayM.Length-1);
if (outputIndex >= 0) Console.WriteLine(arrayM[outputIndex] + "is int the arrayM(Use recursion)");
}
Console.Read();
}
static int BinarySearchRecursion(int[] inputArray, int value, int left, int right)
{
if (left <= right)
{
int mid = (left + right) / 2;
if (inputArray[mid] == value) return mid;
else if (inputArray[mid] > value) return BinarySearchRecursion(inputArray, value, left, mid - 1);
else return BinarySearchRecursion(inputArray, value, mid + 1, right);
}
else return -1;
}
注意
类似的查找方法
- 插值查找
在元素数值均匀分布的有序数组里面, 用插值查找是很快的2。特别的,对绝对均匀分布的数组(相邻元素差值相同), 插值查找用一次比较就能查找成功。
public static int InsertSearch(int[] a, int key)
{
int low = 0;
int high = a.Length - 1;
int mid;
while (a[low] != a[high] && key >= a[low] && key <= a[high]) { // 判断条件很重要, 不能缺少
mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]);
if (key < a[mid]) high = mid - 1;
else if (key > a[mid]) low = mid + 1;
else return mid;
}
if (key == a[low]) return low; // 如果是 2,2,2,2,2这种全部重复元素,返回第一个2
else return -1;
}
注意: 一定要保证两点:
a[low]!=a[high] ( 插值公式里分母是a[high] - a[low],不能等于0)
a[low]<=key<=a[high]
- 斐波那契查找
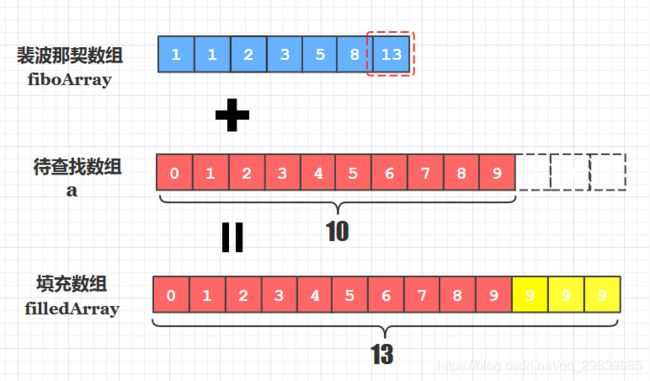
- 根据待查找数组长度确定裴波那契数组的长度(或最大元素值)
- 根据1中长度创建该长度的裴波那契数组,再通过F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)生成裴波那契数列为数组赋值
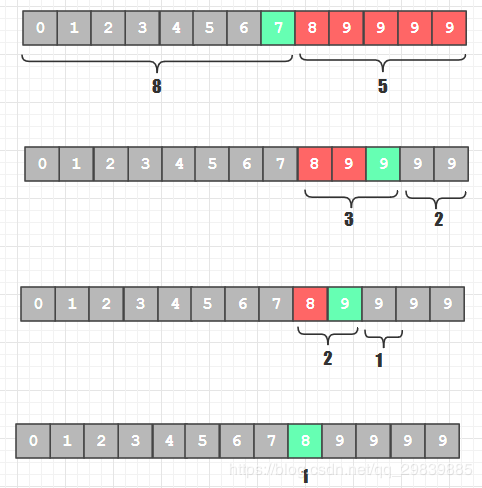
以2中的裴波那契数组的最大值为长度创建填充数组,将原待排序数组元素拷贝到填充数组中来, 如果有剩余的未赋值元素, 用原待排序数组的最后一个元素值填充 - 针对填充数组进行关键字查找, 查找成功后记得判断该元素是否来源于后来填充的那部分元素
//测试代码,未完成!
public static int fibMonaccianSearch(int[] arr,int x)
{
/* Initialize fibonacci numbers */
int fibMMm2 = 0; // (m-2)'th Fibonacci No.
int fibMMm1 = 1; // (m-1)'th Fibonacci No.
int fibM = fibMMm2 + fibMMm1; // m'th Fibonacci
/* fibM is going to store the smallest
Fibonacci Number greater than or equal to n */
while (fibM < arr.Length)
{
fibMMm2 = fibMMm1;
fibMMm1 = fibM;
fibM = fibMMm2 + fibMMm1;
}
// Marks the eliminated range from front
int offset = -1;
/* while there are elements to be inspected.
Note that we compare arr[fibMm2] with x.
When fibM becomes 1, fibMm2 becomes 0 */
while (fibM > 1)
{
// Check if fibMm2 is a valid location
int i = min(offset + fibMMm2, arr.Length - 1);
/* If x is greater than the value at
index fibMm2, cut the subarray array
from offset to i */
if (arr[i] < x) {
fibM = fibMMm1;
fibMMm1 = fibMMm2;
fibMMm2 = fibM - fibMMm1;
offset = i;
}
/* If x is greater than the value at index
fibMm2, cut the subarray after i+1 */
else if (arr[i] > x) {
fibM = fibMMm2;
fibMMm1 = fibMMm1 - fibMMm2;
fibMMm2 = fibM - fibMMm1;
}
/* element found. return index */
else return i;
}
/* comparing the last element with x */
if (fibMMm1 == 1 && arr[offset + 1] == x)
return offset + 1;
/*element not found. return -1 */
return -1;
}
复杂度分析
- 时间复杂度
折半搜索每次把搜索区域减少一半,时间复杂度为 O ( log n ) {\displaystyle O\left(\log n\right)} O(logn)。(n代表集合中元素的个数) - 空间复杂度
O ( 1 ) {\displaystyle O\left(1\right)} O(1)。虽以递归形式定义,但是尾递归,可改写为循环。
在和顺序查找进行比较时,在数据量较大的情况下,如果源数据是有序的,则二分查找法效率高,反之顺序查找效率较高(原因是对源数据进行排序需要耗费很长时间)。 ↩︎
二分搜索在一般的情况下时间复杂度是对数时间,进行 O ( log n ) {\displaystyle O(\log n)} O(logn)次比较操作,插值搜索的最坏时间复杂度是 O ( n ) {\displaystyle O(n)} O(n),平均进行 O ( log ( log n ) ) {\displaystyle O(\log(\log n))} O(log(logn))次比较操作。因为用插值公式计算搜索键值,能使搜索范围比二分法更快缩小。所以除非输入数据数量很少,否则插值搜索比二分搜索与线性搜索更快,但数组必须事先被排序。无论对任何大小的输入数据,插值搜索算法使用的空间复杂度一样是 O ( 1 ) {\displaystyle O(1)} O(1)。 ↩︎