字符串常见面试题
面试相关
特点
- 广泛性
- 可看作是字符类型的数组,与数组的排序、查找、调整有关
- 很多其他类型的面试题可看作是字符串类型的面试题
- 需要掌握的概念
- 回文
- 子串(连续)
- 子序列(不连续)
- 前缀树(Trie 树)
- 后缀树和后缀数组
- 匹配
- 字典序
- 需要掌握的操作
- 与数组有关的操作:增删改查
- 字符替换
- 字符串旋转
注意:用 Java 实现字符串类型题目时,需要掌握 StringBuilder、 StringBuffer 类 与 toCharArray() 方法。
类型
-
规则判断
整数、浮点数、回文等
-
数字运算
int 和 long 所能表达的整数范围有限,所以常会使用字符串实现大整数
与大整数相关的加减乘除操作,需要模拟笔算的过程
-
与数组操作有关
数组有关的调整、排序等操作需要掌握;快速排序的划分过程需要掌握和改写。
-
字符计数
哈希表;定长数组;滑动窗口问题、寻找无重复字符子串问题、计算变位词问题等。
-
动态规划类型
最长公共字串、最长公共子序列、最长回文子串、最长回文子序列
-
搜索类型
宽度优先搜索、深度优先搜索
-
高级算法与数据结构解决的问题
- Manacher 算法解决最长回文子串
- KMP 算法解决字符串匹配
- 前缀树结构
- 后缀树和后缀数组
这类结构较为复杂,通常面试中很少出现。
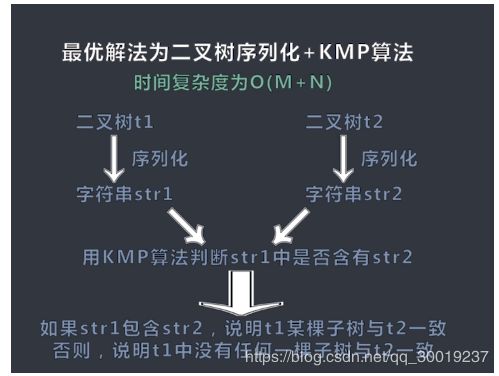
二叉树相同子树
一般解法
遍历匹配:
public boolean HasSubtree(TreeNode root1, TreeNode root2) {
boolean result = false;
//当Tree1和Tree2都不为零的时候,才进行比较。否则直接返回false
if (root2 != null && root1 != null) {
//如果找到了对应Tree2的根节点的点
if (root1.val == root2.val) {
//以这个根节点为为起点判断是否包含Tree2
result = doesTree1HaveTree2(root1, root2);
}
//如果找不到,那么就再去root的左儿子当作起点,去判断时候包含Tree2
if (!result) {
result = HasSubtree(root1.left, root2);
}
//如果还找不到,那么就再去root的右儿子当作起点,去判断时候包含Tree2
if (!result) {
result = HasSubtree(root1.right, root2);
}
}
//返回结果
return result;
}
public boolean doesTree1HaveTree2(TreeNode node1, TreeNode node2) {
//如果Tree2已经遍历完了都能对应的上,返回true
if (node2 == null) {
return true;
}
//如果Tree2还没有遍历完,Tree1却遍历完了。返回false
if (node1 == null) {
return false;
}
//如果其中有一个点没有对应上,返回false
if (node1.val != node2.val) {
return false;
}
//如果根节点对应的上,那么就分别去子节点里面匹配
return doesTree1HaveTree2(node1.left, node2.left) && doesTree1HaveTree2(node1.right, node2.right);
}
字符串解法
// 如果不记录空指针,仅靠前序遍历无法确定二叉树
public boolean chkIdentical(TreeNode A, TreeNode B) {
if (A == null || B == null) return false;
StringBuilder aString = new StringBuilder();
StringBuilder bString = new StringBuilder();
ArrayList<TreeNode> listA = new ArrayList<>();
ArrayList<TreeNode> listB = new ArrayList<>();
// 实际上是模拟栈
listA.add(A);
while (!listA.isEmpty()) {
A = listA.remove(listA.size() - 1);
aString.append(A.val + "!");
if (A.right != null) { // 后出先入
listA.add(A.right);
} else aString.append("#!");
if (A.left != null) {
listA.add(A.left);
} else aString.append("#!");
}
listB.add(B);
while (!listB.isEmpty()) {
B = listB.remove(listB.size() - 1);
bString.append(B.val + "!");
if (B.right != null) {
listB.add(B.right);
} else bString.append("#!");
if (B.left != null) {
listB.add(B.left);
} else bString.append("#!");
}
String bs = bString.toString();
String as = aString.toString();
return as.contains(bs);
}
词语变形
对于两个字符串 A 和 B,如果 A 和 B 中出现的字符种类相同且每种字符出现的次数相同,
则 A 和 B 互为变形词,请设计一个高效算法,检查两给定串是否互为变形词。
给定两个字符串 A 和 B 及他们的长度,请返回一个 bool 值,代表他们是否互为变形词。
思路
解法 1:利用哈希表实现,key 为字符内容,value 为出现次数
解法 2:利用数组实现,value 为数组内容(出现次数),key 为数组下标(值)
实现
// 数组实现
public boolean chkTransform(String a, int lena, String b, int lenb) {
if (a == null || b == null || lena != lenb) {
return false;
}
int[] count = new int[256];
for (int i = 0; i < lena; i++) {
count[a.charAt(i)]++;
}
for (int i = 0; i < lenb; i++) {
if (count[b.charAt(i)]-- == 0) {
return false;
}
}
return true;
}
// 哈希表实现
public boolean chkTransform(String a, int lena, String b, int lenb) {
if (a == null || b == null || lena != lenb) {
return false;
}
HashMap<Character, Integer> mapA = new HashMap<>();
for (int i = 0; i < lena; i++) {
if (!mapA.containsKey(a.charAt(i))) {
mapA.put(a.charAt(i), 1);
} else {
mapA.put(a.charAt(i), mapA.get(a.charAt(i)) + 1);
}
}
HashMap<Character, Integer> mapB = new HashMap<>();
for (int i = 0; i < lenb; i++) {
if (!mapB.containsKey(b.charAt(i))) {
mapB.put(b.charAt(i), 1);
} else {
mapB.put(b.charAt(i), mapB.get(b.charAt(i)) + 1);
}
}
if (mapA.size() != mapB.size())
return false;
for (char c :
mapA.keySet()) {
if (mapB.get(c) != mapA.get(c))
return false;
}
return true;
}
两串旋转
如果对于一个字符串 A,将 A 的前面任意一部分挪到后边去形成的字符串称为 A 的旋转词。
比如 A=“12345”,A 的旋转词有 “12345”,“23451”,“34512”,“45123” 和 “51234”。
对于两个字符串 A 和 B,请判断 A 和 B 是否互为旋转词。
给定两个字符串 A 和 B 及他们的长度 lena,lenb,请返回一个 bool 值,代表他们是否互为旋转词。
思路
若两串互为旋转词,则两串相加所形成的串必定包含两串各自的内容。
实现
public boolean chkRotation(String A, int lena, String B, int lenb) {
String tmp1 = A + A;
String tmp2 = B + B;
return tmp1.contains(B) && tmp2.contains(A);
}
句子逆序
对于一个字符串,请设计一个算法,只在字符串的单词间做逆序调整,
也就是说,字符串由一些由空格分隔的部分组成,你需要将这些部分逆序。
给定一个原字符串 A :“dog loves pig” 和他的长度,请返回逆序后的字符串 “pig loves dog”。
思路
- 首先将句子中所有内容都进行逆序,dog loves pig -> gip sevol god
- 再将每个单词中的所有内容进行逆序, gip sevol god -> pig loves dog
实现
public String reverseSentence(String A, int n) {
char[] words = A.toCharArray();
reverseAllChar(words, 0, n - 1);
int start = 0;
for (int i = 0; i < words.length; i++) {
if (words[i] == ' ') {
reverseAllChar(words, start, i - 1);
start = i + 1;
}
}
reverseAllChar(words, start, words.length - 1);
return String.valueOf(words);
}
public void reverseAllChar(char[] arr, int start, int end) {
while (start < end) {
char tmp = arr[start];
arr[start++] = arr[end];
arr[end--] = tmp;
}
}
字符串移位
对于一个字符串,请设计一个算法,将字符串的长度为 len 的前缀平移到字符串的最后。
给定一个字符串 A 和它的长度,同时给定 len,请返回平移后的字符串。
要求空间复杂度为 O(1),即不能使用辅助数组。
思路
解法 1 :1. len 将数组分为了两部分,首先将前半部分和后半部分分别逆序;
2. 其次将全体逆序
解法 2: 利用两串旋转相同思路实现
实现
public String stringTranslation(String A, int n, int i) {
// 解法 1
char[] arr = A.toCharArray();
reverseAllChar(arr, 0, i - 1);
reverseAllChar(arr, i, n - 1);
reverseAllChar(arr, 0, n - 1);
return String.valueOf(arr);
// 解法 2
//return (A + A).substring(i, i + n);
}
public void reverseAllChar(char[] arr, int start, int end) {
while (start < end) {
char tmp = arr[start];
arr[start++] = arr[end];
arr[end--] = tmp;
}
}
拼接最小字典
对于一个给定的字符串数组,请找到一种拼接顺序,
使所有小字符串拼接成的大字符串是所有可能的拼接中字典序最小的。
给定一个字符串数组 strs,同时给定它的大小,请返回拼接成的串。
思路
不要单个字符串比较,应组合比较:若 str1 + str2 < str2 + str1,则 str1 应排在 str2 之前
实现
public class MyComparator implements Comparator<String> {
public int compare(String a, String b) {
return (a + b).compareTo(b + a);
}
}
public String findSmallest(String[] strs, int n) {
if (strs == null || n == 0) {
return "";
}
// 根据新的比较方式排序
Arrays.sort(strs, new MyComparator());
StringBuilder res = new StringBuilder();
for (String str : strs) {
res.append(str);
}
return res.toString();
}
空格替换
请编写一个方法,将字符串中的空格全部替换为 “%20”。
假定该字符串有足够的空间存放新增的字符,并且知道字符串的真实长度 (小于等于 1000),
同时保证字符串由大小写的英文字母组成。
给定一个 string iniString 为原始的串,以及串的长度 int len, 返回替换后的 string。
思路
解法 1 : 利用变长 StringBuffer
解法 2 :根据空格数重新构造新的定长数组,在此数组上完成操作
实现
// 解法 1
public static String replaceBlank(StringBuffer stringBuffer) {
StringBuffer str = new StringBuffer();
for (int i = 0; i < stringBuffer.length(); i++) {
if (stringBuffer.charAt(i) == ' ') {
str.append('%');
str.append('2');
str.append('0');
} else {
str.append(stringBuffer.charAt(i));
}
}
return str.toString();
}
// 解法 2
public static String replaceBlank(String iniString, int len) {
char[] arr = iniString.toCharArray();
int count = 0;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == ' ') {
count++;
}
}
char[] res = new char[count * 2 + len];
int resLen = res.length - 1;
for (int i = len - 1; i >= 0; i--) {
if (arr[i] == ' ') {
res[resLen--] = '0';
res[resLen--] = '2';
res[resLen--] = '%';
} else res[resLen--] = arr[i];
}
return String.valueOf(res);
}
合法括号序列判断
思路
解法 1 :利用栈
解法 2 :简单利用字符串计数
实现
// 解法 1
public boolean chkParenthesis(String strR, int n)
for (int i = 0; i < strR.length(); i++) {
if (Pattern.matches("[a-z]", strR.charAt(i) + "")) {
continue;
}
if (strR.charAt(i) == '(' || strR.charAt(i) == '{'
|| strR.charAt(i) == '[' ) {
stack.push(strR.charAt(i));
} else if (isMatch(strR.charAt(i)) ) {
stack.pop();
} else {
System.out.println("error: can't match!!");
break;
}
System.out.println(stack.toString());
}
}
public boolean isMatch(Character c) {
if (this.isEmpty()) {
return false;
}
switch (this.top()) {
case '(':
if (c == ')')
return true;
break;
case '[':
if (c == ']')
return true;
break;
case '{':
if (c == '}')
return true;
break;
}
return false;
}
// 解法 2
public boolean chkParenthesis(String A, int n) {
char[] arr = A.toCharArray();
int flag = 0;
for (int i = 0; i < arr.length; i++) {
if (arr[i] != ')' && arr[i] != '(') {
return false;
}
if (arr[i] == '(')
flag++;
else if (arr[i] == ')' && --flag < 0)
return false;
}
return flag == 0;
}
最长无重复字串
思路
- 针对第 i 个结点
- 设定一个哈希表 preIndex 保存该结点值上一次出现的位置 posPre
- 设定一个长度 longest 保存从 i - 1 开始的最长无重复字串长度
- 将每个结点放入 preIndex
- posPre 的下一位设为 posA
- 如果 posA 到 i 的距离小于最长无重复字串长度,则长度自增
- 如果 posA 到 i 的距离大于最长无重复字串长度,则将该长度设为 i - pos + 1
- 取最长
思路相同,解法 1 利用哈希表,解法 2 利用数组。
实现
// 解法 1
public int longestSubstring(String A, int n) {
if (A == null || n == 0) {
return 0;
}
char[] arr = A.toCharArray();
// 保存结点
HashMap<Character, Integer> preIndex = new HashMap<>();
int longest = 0, posA, res = 0;
for (int i = 0; i < n; i++) {
if (!preIndex.containsKey(arr[i])) {
preIndex.put(arr[i], i);
longest++;
} else {
posA = preIndex.get(arr[i]) + 1;
if (posA > i - longest) {
longest = i - posA + 1;
} else {
longest++;
}
preIndex.put(arr[i], i);
}
if (longest > res) {
res = longest;
}
}
return res;
}
// 解法 2
public int longestSubstring(String A, int n) {
if (A == null || n == 0) {
return 0;
}
char[] chas = A.toCharArray();
int[] map = new int[256];
for (int i = 0; i < 256; i++) {
map[i] = -1;
}
int len = 0;
int pre = -1;
int cur = 0;
for (int i = 0; i < n; i++) {
pre = Math.max(pre, map[chas[i]]);
cur = i - pre;
len = Math.max(len, cur);
map[chas[i]] = i;
}
return len;
}