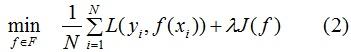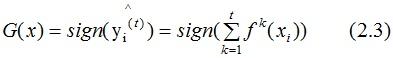XGBoost

原理

xbt中的目标函数是有个正则项惩罚复杂模型;
将树拆分成结构部分q和叶子部分权重w;

构建最优模型的一般方法是最小化训练数据的损失函数，我们用字母 L表示，如下式：

式（1）称为经验风险最小化，训练得到的模型复杂度较高。当训练数据较小时，模型很容易出现过拟合问题。

因此，为了降低模型的复杂度，常采用下式：

其中J(f)为模型的复杂度，式（2）称为结构风险最小化，结构风险最小化的模型往往对训练数据以及未知的测试数据都有较好的预测 。

应用：决策树的生成和剪枝分别对应了经验风险最小化和结构风险最小化，XGBoost的决策树生成是结构风险最小化的结果，后续会详细介绍。

Boosting方法的回归思想

Boosting法是结合多个弱学习器给出最终的学习结果，不管任务是分类或回归，我们都用回归任务的思想来构建最优Boosting模型 。

回归思想：把每个弱学习器的输出结果当成连续值，这样做的目的是可以对每个弱学习器的结果进行累加处理，且能更好的利用损失函数来优化模型。

假设

是第 t 轮弱学习器的输出结果，

是模型的输出结果，

是实际输出结果，表达式如下：

上面两式就是加法模型，都默认弱学习器的输出结果是连续值。因为回归任务的弱学习器本身是连续值，所以不做讨论，下面详细介绍分类任务的回归思想。

 

分类任务的回归思想：

根据2.1式的结果，得到最终的分类器：

分类的损失函数一般选择指数函数或对数函数，这里假设损失函数为对数函数，学习器的损失函数是

若实际输出结果yi=1，则：

求（2.5）式对

的梯度，得：

负梯度方向是损失函数下降最快的方向，（2.6）式取反的值大于0，因此弱学习器是往增大

的方向迭代的，图形表示为：

如上图，当样本的实际标记 yi 是 1 时，模型输出结果

随着迭代次数的增加而增加（红线箭头），模型的损失函数相应的减小；当样本的实际标记 yi 是 -1时，模型输出结果

随着迭代次数的增加而减小（红线箭头），模型的损失函数相应的减小 。这就是加法模型的原理所在，通过多次的迭代达到减小损失函数的目的。

 

小结：Boosting方法把每个弱学习器的输出看成是连续值，使得损失函数是个连续值，因此可以通过弱学习器的迭代达到优化模型的目的，这也是集成学习法加法模型的原理所在 。

XGBoost算法的目标函数推导

目标函数，即损失函数，通过最小化损失函数来构建最优模型，由第一节可知， 损失函数应加上表示模型复杂度的正则项，且XGBoost对应的模型包含了多个CART树，因此，模型的目标函数为：

（3.1）式是正则化的损失函数，等式右边第一部分是模型的训练误差，第二部分是正则化项，这里的正则化项是K棵树的正则化项相加而来的。

CART树的介绍：

上图为第K棵CART树，确定一棵CART树需要确定两部分，第一部分就是树的结构，这个结构将输入样本映射到一个确定的叶子节点上，记为

。第二部分就是各个叶子节点的值，q(x)表示输出的叶子节点序号，

表示对应叶子节点序号的值。由定义得：

树的复杂度定义

XGBoost法对应的模型包含了多棵cart树，定义每棵树的复杂度：

其中T为叶子节点的个数，||w||为叶子节点向量的模 。γ表示节点切分的难度，λ表示L2正则化系数。

如下例树的复杂度表示：

 

目标函数推导

根据（3.1）式，共进行t次迭代的学习模型的目标函数为：

泰勒公式的二阶导近似表示：

令

为Δx，则（3.5）式的二阶近似展开：

其中：

表示前t-1棵树组成的学习模型的预测误差，gi和hi分别表示预测误差对当前模型的一阶导和二阶导 ，当前模型往预测误差减小的方向进行迭代。

忽略（3.8）式常数项，并结合（3.4）式，得：

通过（3.2）式简化（3.9）式：

（3.10）式第一部分是对所有训练样本集进行累加，因为所有样本都是映射为树的叶子节点，我们换种思维，从叶子节点出发，对所有的叶子节点进行累加，得：

令

Gj 表示映射为叶子节点 j 的所有输入样本的一阶导之和，同理，Hj表示二阶导之和。

得：

对于第 t 棵CART树的某一个确定结构（可用q(x)表示），其叶子节点是相互独立的，Gj和Hj是确定量，因此，（3.12）可以看成是关于叶子节点的一元二次函数 。最小化（3.12）式，得：

得到最终的目标函数：

（3.14）也称为打分函数(scoring function)，它是衡量树结构好坏的标准，值越小，代表这样的结构越好 。我们用打分函数选择最佳切分点，从而构建CART树。

CART回归树的构建方法

上节推导得到的打分函数是衡量树结构好坏的标准，因此，可用打分函数来选择最佳切分点。首先确定样本特征的所有切分点，对每一个确定的切分点进行切分，切分好坏的标准如下：

Gain表示单节点obj*与切分后的两个节点的树obj*之差，遍历所有特征的切分点，找到最大Gain的切分点即是最佳分裂点，根据这种方法继续切分节点，得到CART树。若 γ 值设置的过大，则Gain为负，表示不切分该节点，因为切分后的树结构变差了。γ值越大，表示对切分后obj下降幅度要求越严，这个值可以在XGBoost中设定。

分裂节点算法

XGBoost与GDBT的区别

1. XGBoost生成CART树考虑了树的复杂度，GDBT未考虑，GDBT在树的剪枝步骤中考虑了树的复杂度。

2. XGBoost是拟合上一轮损失函数的二阶导展开，GDBT是拟合上一轮损失函数的一阶导展开，因此，XGBoost的准确性更高，且满足相同的训练效果，需要的迭代次数更少。

3. XGBoost与GDBT都是逐次迭代来提高模型性能，但是XGBoost在选取最佳切分点时可以开启多线程进行，大大提高了运行速度。

直观上看，目标要求预测误差尽量小，叶子节点尽量少，节点数值尽量不极端（这个怎么看，如果某个样本label数值为4，那么第一个回归树预测3，第二个预测为1；另外一组回归树，一个预测2，一个预测2，那么倾向后一种，为什么呢？前一种情况，第一棵树学的太多，太接近4，也就意味着有较大的过拟合的风险）

ok，听起来很美好，可是怎么实现呢，上面这个目标函数跟实际的参数怎么联系起来，记得我们说过，回归树的参数:（1）选取哪个feature分裂节点呢；（2）节点的预测值（总不能靠取平均值这么粗暴不讲道理的方式吧，好歹高级一点）。上述形而上的公式并没有“直接”解决这两个，那么是如何间接解决的呢？

先说答案：贪心策略+最优化（二次最优化，恩你没看错）

通俗解释贪心策略：就是决策时刻按照当前目标最优化决定，说白了就是眼前利益最大化决定，“目光短浅”策略，他的优缺点细节大家自己去了解，经典背包问题等等。

这里是怎么用贪心策略的呢，刚开始你有一群样本，放在第一个节点，这时候T=1T=1，ww多少呢，不知道，是求出来的，这时候所有样本的预测值都是ww（这个地方自己好好理解，决策树的节点表示类别，回归树的节点表示预测值）,带入样本的label数值，此时loss function变为 
    

如果这里的l(w−yi)l(w−yi)误差表示用的是平方误差，那么上述函数就是一个关于ww的二次函数求最小值，取最小值的点就是这个节点的预测值，最小的函数值为最小损失函数。
暂停下，这里你发现了没，二次函数最优化！ 
要是损失函数不是二次函数咋办，哦，泰勒展开式会否？，不是二次的想办法近似为二次。

接着来，接下来要选个feature分裂成两个节点，变成一棵弱小的树苗，那么需要：（1）确定分裂用的feature，how？最简单的是粗暴的枚举，选择loss function效果最好的那个（关于粗暴枚举，Xgboost的改良并行方式咱们后面看）；（2）如何确立节点的ww以及最小的loss function，大声告诉我怎么做？对，二次函数的求最值（细节的会注意到，计算二次最值是不是有固定套路，导数=0的点，ok）

那么节奏是，选择一个feature分裂，计算loss function最小值，然后再选一个feature分裂，又得到一个loss function最小值…你枚举完，找一个效果最好的，把树给分裂，就得到了小树苗。

在分裂的时候，你可以注意到，每次节点分裂，loss function被影响的只有这个节点的样本，因而每次分裂，计算分裂的增益（loss function的降低量）只需要关注打算分裂的那个节点的样本

接下来，继续分裂，按照上述的方式，形成一棵树，再形成一棵树，每次在上一次的预测基础上取最优进一步分裂/建树，是不是贪心策略？！

凡是这种循环迭代的方式必定有停止条件，什么时候停止呢： 
（1）当引入的分裂带来的增益小于一个阀值的时候，我们可以剪掉这个分裂，所以并不是每一次分裂loss function整体都会增加的，有点预剪枝的意思（其实我这里有点疑问的，一般后剪枝效果比预剪枝要好点吧，只不过复杂麻烦些，这里大神请指教，为啥这里使用的是预剪枝的思想，当然Xgboost支持后剪枝），阈值参数为γγ正则项里叶子节点数T的系数（大神请确认下）； 
（2）当树达到最大深度时则停止建立决策树，设置一个超参数max_depth，这个好理解吧，树太深很容易出现的情况学习局部样本，过拟合； 
（3）当样本权重和小于设定阈值时则停止建树，这个解释一下，涉及到一个超参数-最小的样本权重和min_child_weight，和GBM的 min_child_leaf 参数类似，但不完全一样，大意就是一个叶子节点样本太少了，也终止同样是过拟合； 
（4）貌似看到过有树的最大数量的…这个不确定 
具体数学推导细节（只要是那个节点分裂增益计算的公式），请参看作者（论文作者哦）介绍，很细致！http://www.52cs.org/?p=429，上面那个也可以 
问题1：节点分裂的时候是按照哪个顺序来的，比如第一次分裂后有两个叶子节点，先裂哪一个？ 
答案：呃，同一层级的（多机）并行，确立如何分裂或者不分裂成为叶子节点，来源 
https://wenku.baidu.com/view/44778c9c312b3169a551a460.html

是最优化求出来的，不是啥平均值或规则指定的，这个算是一个思路上的新颖吧；

正则化防止过拟合的技术，上述看到了，直接loss function里面就有；

支持自定义loss function，哈哈，不用我多说，只要能泰勒展开（能求一阶导和二阶导）就行，你开心就好；

支持并行化，这个地方有必要说明下，因为这是xgboost的闪光点，直接的效果是训练速度快，boosting技术中下一棵树依赖上述树的训练和预测，所以树与树之间应该是只能串行！那么大家想想，哪里可以并行？！ 
没错，在选择最佳分裂点，进行枚举的时候并行！（据说恰好这个也是树形成最耗时的阶段）

Attention：同层级节点可并行。具体的对于某个节点，节点内选择最佳分裂点，候选分裂点计算增益用多线程并行。—–

较少的离散值作为分割点倒是很简单，比如“是否是单身”来分裂节点计算增益是很easy，但是“月收入”这种feature，取值很多，从5k~50k都有，总不可能每个分割点都来试一下计算分裂增益吧？（比如月收入feature有1000个取值，难道你把这1000个用作分割候选？缺点1：计算量，缺点2：出现叶子节点样本过少，过拟合）我们常用的习惯就是划分区间，那么问题来了，这个区间分割点如何确定（难道平均分割），作者是这么做的：

方法名字：Weighted Quantile Sketch 
大家还记得每个样本在节点（将要分裂的节点）处的loss function一阶导数gigi和二阶导数hihi，衡量预测值变化带来的loss function变化，举例来说，将样本“月收入”进行升序排列，5k、5.2k、5.3k、…、52k，分割线为“收入1”、“收入2”、…、“收入j”，满足(每个间隔的样本的hihi之和/总样本的hihi之和）为某个百分比ϵϵ（我这个是近似的说法），那么可以一共分成大约1/ϵ1/ϵ个分裂点。 
而且，有适用于分布式的算法设计；

XGBoost还特别设计了针对稀疏数据的算法， 
假设样本的第i个特征缺失时，无法利用该特征对样本进行划分，这里的做法是将该样本默认地分到指定的子节点，至于具体地分到哪个节点还需要某算法来计算，

算法的主要思想是，分别假设特征缺失的样本属于右子树和左子树，而且只在不缺失的样本上迭代，分别计算缺失样本属于右子树和左子树的增益，选择增益最大的方向为缺失数据的默认方向（咋一看如果缺失情况为3个样本，那么划分的组合方式岂不是有8种？指数级可能性啊，仔细一看，应该是在不缺失样本情况下分裂后（有大神的请确认或者修正），把第一个缺失样本放左边计算下loss function和放右边进行比较，同样对付第二个、第三个…缺失样本，这么看来又是可以并行的？？）；

可实现后剪枝
交叉验证，方便选择最好的参数，early stop，比如你发现30棵树预测已经很好了，不用进一步学习残差了，那么停止建树。

行采样、列采样，随机森林的套路（防止过拟合）

Shrinkage，你可以是几个回归树的叶子节点之和为预测值，也可以是加权，比如第一棵树预测值为3.3，label为4.0，第二棵树才学0.7，….再后面的树还学个鬼，所以给他打个折扣，比如3折，那么第二棵树训练的残差为4.0-3.3*0.3=3.01，这就可以发挥了啦，以此类推，作用是啥，防止过拟合，如果对于“伪残差”学习，那更像梯度下降里面的学习率；

xgboost还支持设置样本权重，这个权重体现在梯度g和二阶梯度h上，是不是有点adaboost的意思，重点关注某些样本

优缺点

Xgboost第一感觉就是防止过拟合+各种支持分布式/并行，所以一般传言这种大杀器效果好（集成学习的高配）+训练效率高（分布式），与深度学习相比，对样本量和特征数据类型要求没那么苛刻，适用范围广。

说下GBDT：有两种描述版本，把GBDT说成一个迭代残差树，认为每一棵迭代树都在学习前N-1棵树的残差；把GBDT说成一个梯度迭代树，使用梯度迭代下降法求解，认为每一棵迭代树都在学习前N-1棵树的梯度下降值。有说法说前者是后者在loss function为平方误差下的特殊情况。这里说下我的理解，仍然举个例子：第一棵树形成之后，有预测值y^iy^i，真实值（label）为yiyi，前者版本表示下一棵回归树根据样本(xi,yi−y^i)(xi,yi−y^i)进行学习，后者的意思是计算loss function在第一棵树预测值附近的梯度负值作为新的label，也就是对应xgboost中的−gi−gi
这里真心有个疑问： 
Xgboost在下一棵树拟合的是残差还是负梯度，还是说是一阶导数+二阶导数，−gi(1+hi)−gi(1+hi)?可能人蠢，没看太懂，换句话说GBDT残差树群有一种拟合的（输入样本）是(xi,yi−y^i)(xi,yi−y^i),还一种拟合的是(xi,−gi)(xi,−gi)，Xgboost呢？

Xgboost和深度学习的关系，陈天奇在Quora上的解答如下： 
不同的机器学习模型适用于不同类型的任务。深度神经网络通过对时空位置建模，能够很好地捕获图像、语音、文本等高维数据。而基于树模型的XGBoost则能很好地处理表格数据，同时还拥有一些深度神经网络所没有的特性（如：模型的可解释性、输入数据的不变性、更易于调参等）。 
这两类模型都很重要，并广泛用于数据科学竞赛和工业界。举例来说，几乎所有采用机器学习技术的公司都在使用tree boosting，同时XGBoost已经给业界带来了很大的影响。

关键参数

1）objective [ default=reg:linear ] 定义学习任务及相应的学习目标，可选的目标函数如下：

• “reg:linear” –线性回归。
• “reg:logistic” –逻辑回归。
• “binary:logistic” –二分类的逻辑回归问题，输出为概率。
• “binary:logitraw” –二分类的逻辑回归问题，输出的结果为wTx。
• “count:poisson” –计数问题的poisson回归，输出结果为poisson分布。 在poisson回归中，max_delta_step的缺省值为0.7。(used to safeguard optimization)
• “multi:softmax” –让XGBoost采用softmax目标函数处理多分类问题，同时需要设置参数num_class（类别个数）
• “multi:softprob” –和softmax一样，但是输出的是ndata * nclass的向量，可以将该向量reshape成ndata行nclass列的矩阵。没行数据表示样本所属于每个类别的概率。
• “rank:pairwise” –set XGBoost to do ranking task by minimizing the pairwise loss

（2）’eval_metric’ The choices are listed below，评估指标:

• “rmse”: root mean square error
• “logloss”: negative log-likelihood
• “error”: Binary classification error rate. It is calculated as #(wrong cases)/#(all cases). For the predictions, the evaluation will regard the instances with prediction value larger than 0.5 as positive instances, and the others as negative instances.
• “merror”: Multiclass classification error rate. It is calculated as #(wrong cases)/#(all cases).
• “mlogloss”: Multiclass logloss
• “auc”: Area under the curve for ranking evaluation.
• “ndcg”:Normalized Discounted Cumulative Gain
• “map”:Mean average precision
• “ndcg@n”,”map@n”: n can be assigned as an integer to cut off the top positions in the lists for evaluation.
• “ndcg-“,”map-“,”ndcg@n-“,”map@n-“: In XGBoost, NDCG and MAP will evaluate the score of a list without any positive samples as 1. By adding “-” in the evaluation metric XGBoost will evaluate these score as 0 to be consistent under some conditions.

（3）lambda [default=0] L2 正则的惩罚系数

（4）alpha [default=0] L1 正则的惩罚系数

（5）lambda_bias 在偏置上的L2正则。缺省值为0（在L1上没有偏置项的正则，因为L1时偏置不重要）

（6）eta [default=0.3] 
为了防止过拟合，更新过程中用到的收缩步长。在每次提升计算之后，算法会直接获得新特征的权重。 eta通过缩减特征的权重使提升计算过程更加保守。缺省值为0.3 
取值范围为：[0,1]

（7）max_depth [default=6] 数的最大深度。缺省值为6 ，取值范围为：[1,∞]

（8）min_child_weight [default=1] 
孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束。在现行回归模型中，这个参数是指建立每个模型所需要的最小样本数。该成熟越大算法越conservative 
取值范围为: [0,∞]