非线性逻辑回归的代码实现（梯度下降法）

非线性逻辑回归的代码实现（梯度下降法）

当我们需要分类这样的数据集的时候，线性的逻辑回归就派不上用场了
前期的代码模块都与线性逻辑回归的步骤一致。
线性逻辑回归的代码实现：
https://mp.csdn.net/mdeditor/90899227#

载入数据

data = np.genfromtxt(r'data.txt',delimiter=',')
x_data = data[:, :-1]
y_data = data[:, -1, np.newaxis]

对原始数据画图

def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同数据
    for i in range(len(x_data)):
        if y_data[i] == 0:
            x0.append(x_data[i, 0])
            y0.append(x_data[i, 1])
        else:
            x1.append(x_data[i, 0])
            y1.append(x_data[i, 1])
    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0, scatter1], labels=['label0', 'label1'], loc='best')
plot()
plt.show()

生成非线性项：

from sklearn.preprocessing import PolynomialFeatures
# 定义多项式回归，degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=3)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)

利用sklearn.preprocessing import PolynomialFeatures来构建特征项，其中degree控制多项式的度。
例如，如果有a，b两个特征，那么它的2次多项式为（1,a,b,a^2,ab, b^2）
利用代码来看一看，这里a=2,b=3,degree=3,

所以它打印出来的是1,a,b,a²,ab,b²,a³,a²b,ab²,b³

定义sigmoid函数、代价函数、梯度下降法

def sigmoid(x):
    return 1.0/(1+np.exp(-x))


def cost(xMat, yMat, ws):
    left = np.multiply(yMat, np.log(1-sigmoid(xMat*ws)))
    right = np.multiply(1-yMat, np.log(1-sigmoid(xMat * ws)))
    return np.sum(left + right) / -(len(xMat))


def gradDscent(xArr, yArr):
    if scale == True:
        xArr = preprocessing(xArr)
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)
    lr = 0.03
    epochs = 50000
    costList = []
    #计算数据列数，有几列就有几个权值
    m, n = np.shape(xMat)
    #初始化权值
    ws = np.mat(np.ones((n, 1)))
    for i in range(epochs+1):
        # xMat和weights矩阵相乘
        h = sigmoid(xMat*ws)
        # 计算误差
        ws_grad = xMat.T*(h-yMat)/m
        ws = ws - lr * ws_grad
        if i % 50 == 0:
            costList.append(cost(xMat, yMat, ws))
    return ws, costList

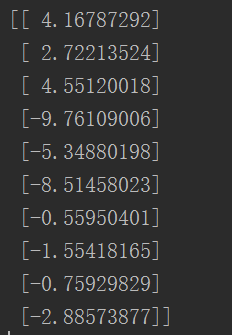
得到degree=3时各项的权值

#训练模型，得到权值和cost值的变化
ws, costList = gradDscent(x_poly, y_data)
print(ws)

至此，结果已经得出。
接下来就是作图

作图

# 获取数据所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1

# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02))
# 进行判断
z = sigmoid(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]).dot(np.array(ws)))
# ravel与flatten类似,多维数据转一维            
for i in range(len(z)):
    if z[i] > 0.5:
        z[i] = 1
    else:
        z[i] = 0
z = z.reshape(xx.shape)

注：ravel与flatten类似,多维数据转一维
flatten不会改变原始数据，ravel会改变原始数据

做等高线图观察

z的值只会是0或1，在等高线图中，z代表高度，所以属于不同类的数据可以很直观地观察出来。

cs = plt.contourf(xx, yy, z)
plot()
plt.show()

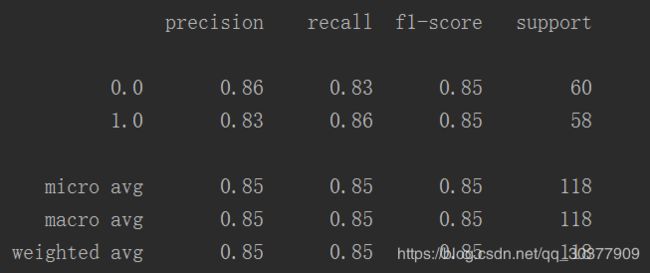
预测

def predict(x_data, ws):
    xMat = np.mat(x_data)
    ws = np.mat(ws)
    return [1 if x >= 0.5 else 0 for x in sigmoid(xMat*ws)]
predictions = predict(x_poly, ws)
print(classification_report(y_data, predictions))

结束