【机器学习】支持向量机(SVM)

参考 李航-统计学习方法

支持向量机是一种分类算法，1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

1、算法思想

首先来通过一个故事介绍一下支持向量机，刚学习svm的时候在知乎上看到一个通俗易懂的例子：
一个勇者为了救公主遇到了魔王boss，魔王给他设置了一个考验如果能勇者能通过考验就把公主还给他，桌面上摆放了一些红球和篮球，要求勇者用一根棍分开它们，要求：尽量在放更多球之后，仍然适用。
经过不断调整位置是木棍与两侧的球尽可能保持最大的距离就可以解决这个问题。

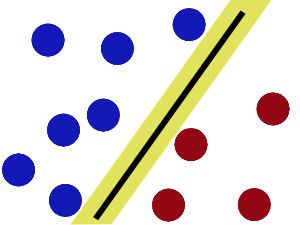
然后大魔王又升级了这个挑战，他将两种球混乱摆放使得无法使用一根直木棍来分开这两种球

这当然难不倒我们的勇者，勇者用力一拍桌子把球都拍到空中然后在空中迅速的抓起一张纸塞了进去将两种颜色的球分开了

魔王在天上向下看看到了这样的画面

魔王大吃一惊，我类个去居然还有这种操作，在下服了，只能把公主还给了勇者

最后无聊的人们把这些球叫做(数据)data，把棍子叫(分类器)classifier, 找到最大间隙的trick叫做(优化)optimization，拍桌子叫做(核变换)kernelling, 那张纸叫做(超平面)hyperplane。

经过以上例子我们可就能理解svm的作用了，如果数据是线性可分的，我们就只用一条直线就可以将他们分开，这个时候只需要将边上的球到直线的间隔最大化就好了，这就是优化过程。
当我们遇到线性不可分的问题的时候，就用使用一种拍桌子的trick，也就是对应我们的核变换(kernel)，然后在高维空间使用超平面将数据分类。

2、公式推导

先说明几个概念

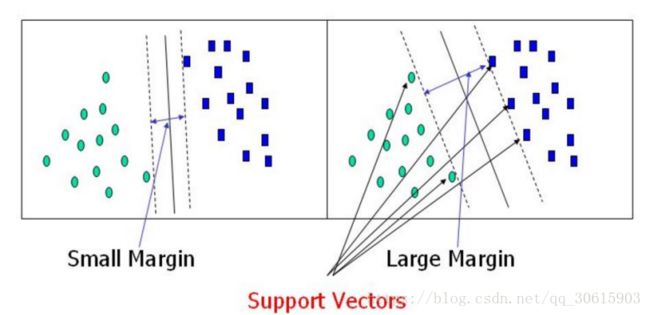
决策边界：就是图中间的那条线，用来判断分类
支持向量：就是指图中左右两边最接近决策边界的数据
最大间隔：选择离决策边界最远的支持向量，也就是我们要寻找的最优解

首先考虑二维空间下，决策方程定义为 $y=wx+b$ 对应 $R^n$中的一个超平面 S 其中 w 是超平面的法向量 b 截距

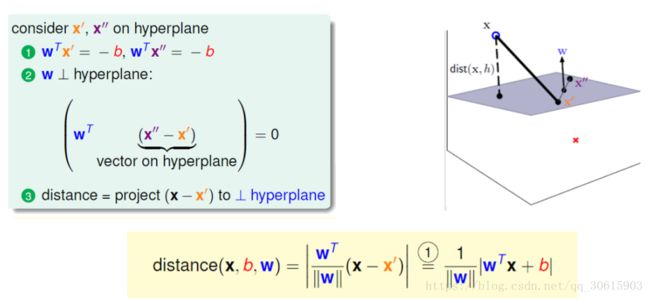
根据点到面距离求法我们能得到 $distance=\frac{1}{||w||}|w{x}_i+b|$

我们考虑样本的类别正样本时 $Y=+1$ 负样本时 $Y=-1$ 这时可以将绝对值展开，可以在外面乘以$y_i$ 则空间$R^n$上任意一样本点到S面的距离可定义为

$r_i=\frac{1}{||w||}(w{x}_i+b)y_i$

因为我们要最大间隔，所以优化目标为

$argma{x}_{w,b}[\frac{1}{||w||}mi{n}_i(y_i(w{x}_i+b))]$

argmax是最大距离min是找最近的支持向量，因为$y_i(w{x}_i+b)=1$ 所以就只剩下

$ma{x}_{w,b}\frac{1}{||w||}$

因为我们学习算法一般喜欢求最小值损失所以将问题转化为

$mi{n}_{w,b}\frac{1}{2}||w|{|}^2$

为了方便求导我们就乘了$\frac{1}{2}$ 平方也是为了求导因为$||w||$是2范数是带根号的也是为了方便求导

求解

问题已经转换为凸二次规划的问题所以可用拉格朗日对偶法求解，前提是我们的目标函数必须是凸函数，因为只有凸函数才能保证存在全局最优解，此时与凸优化联系起来，我们的超平面就是一个凸的。求最优解的问题通常存在以下几个类型

1)无约束: 无约束情况下目标函数为$minf(x)$ 直接使用费马引理对目标函数求导解极值即可
2)等式约束：存在等式$h_j(x),j=1,2,...m$的情况下，需要使用拉格朗日乘子法对等式引入乘子向量与 $minf(x)$ 构造成新的目标函数求解。
3)不等约束：存在不等约束$g_i(x)<=0,i=1,2...n$，可能还有等式约束$h_j(x),j=1,2,...m$，此时同样需要将这些约束与乘子向量构造新的目标函数，通过KKT条件可解出最优值的必要条件。
【kkt条件】

• 经过拉格朗日函数处理之后对x求导为0
• $h_i(x)=0$
• $g_j(x)<=0$

我们的要求解的函数为
$mi{n}_{w,b}\frac{1}{2}||w|{|}^2$
$s.t.y_i(w{x}_i+b)>=1,i=1,2,...n$(正负样本为-1，1，为了寻找最大间隔所以要服从该条件)
根据不等约束求解方法，首先构造目标函使用拉格朗日乘子法将问题的约束条件转换为无约束的目标函数

$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{\alpha }_i(y_i(w{x}_i+b)-1)$$

原问题就转化为求解 $mi{n}_{w,b}ma{x}_{\alpha }L(w,b,\alpha )$ 因为这样不好求解就根据拉格朗日对偶性，将问题再次转化为求解$ma{x}_{\alpha }mi{n}_{w,b}L(w,b,\alpha )$

对w求偏导：$\frac{\partial L}{\partial w}=0\to w={\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i$
对b求偏导：$\frac{\partial L}{\partial b}=0\to 0={\sum }_{i=1}^n{\alpha }_i{y}_i$

代入原式$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-{\sum }_{i=1}^N{\alpha }_i(y_i(w{x}_i+b)-1)$
解得

$mi{n}_{w,b}L(w,b,\alpha )=\frac{1}{2}{w}^{T}w-w^T{\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i-{\sum }_{i=1}^n{\alpha }_i{y}_i+{\sum }_{i=1}^N{\alpha }_i$
$mi{n}_{w,b}L(w,b,\alpha )={\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}({\sum }_{i=1}^n{\alpha }_i{y}_i{x}_i{)}^T{\sum }_{i=1}^N{\alpha }_i{y}_i{x}_i$
$mi{n}_{w,b}L(w,b,\alpha )={\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}({\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i^T{x}_j))$

以上就完成了对$mi{n}_{w,b}L(w,b,\alpha )$的求解
然后剩下$ma{x}_{\alpha }L(w,b,\alpha )={\sum }_{i=1}^n{\alpha }_i-\frac{1}{2}({\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i^T{x}_j))$
之前说过习惯性求最小所以将问题转化，所以转化之后的目标函数如下
$$mi{n}_{\alpha }L(w,b,\alpha )=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i^T{x}_j)-\sum _{i=1}^n{\alpha }_i$$
$s.t.{\alpha }_i>=0,i=1,2,3.....n$
$s.t.{\sum }_{i=1}^n{\alpha }_i{y}_i=0$

软间隔

上述条件是假设在数据完全线性可分的，当数据不完全线性可分存在噪声的时候就需要我们引入松弛因子

引入松弛因子后就变成 $y_i(w{x}_i+b)>=1-{\xi }_i$
同时目标函数也会发生改变 $mi{n}_{w,b}\frac{1}{2}||w|{|}^2+C{\sum }_{i=1}^n{\xi }_i$ 其中C是需要我们自己进行制定的参数，当C很大时意味着严格不允许有错误，当C很小的时候意味着我们允许出现更大的错误。

同样的解法此时目标函数如下

3、核函数

以上都是针对二维平面上分类方式，当我们遇到低维不可分的情况时候，就要拿出我们的杀手锏核变换了。

之前的目标函数为
$$L(w,b,\alpha )=\frac{1}{2}\sum _{i=1}^n\sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i^T{x}_j)-\sum _{i=1}^n{\alpha }_i$$
此时我们就可以将括号内进行替换

$L(w,b,\alpha )=\frac{1}{2}{\sum }_{i=1}^n{\sum }_{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j(\varphi (x_i)\varphi (x_j))-{\sum }_{i=1}^n{\alpha }_i$

ϕ(x)表示将x映射到高维空间后的特征向量，$\varphi (x_i)\varphi (x_j)$表示高维空间上点的内积，其中，xi和xj分别是原始空间中的点。由于将原始空间中的点映射之后维度会扩大，所以实际计算这样的内积的时候其实是很困难的。那么我们为了避开这样的障碍，可以设想这样一个函数：

$K(x_i,x_j)=\varphi (x_i)\varphi (x_j)$

这样就可以将高维空间的内积映射到原来的维度上进行计算。

常用的核函数有
线性核
$k(x,y)=x^T\ast y$
多项式核（Polynomial Kernel）
$k(x,y)=(x\ast y+1{)}^p$
径向基核函数（Radial Basis Function）
$k(x,y)=exp(-\gamma ||x-y|{|}^2)$
也叫高斯核（Gaussian Kernel），因为可以看成如下核函数的领一个种形式：
$k(x,y)=exp(-\frac{||x-y|{|}^2)}{2{\sigma }^2}$
SMO算法
SMO是一种快速的支持向量机算法，特点是不断的将二次规划问题分解为只有两个变量的二次规划子问题。具体推导篇幅过长就不在此篇解释了