Prim算法求最小生成树的c++代码实现

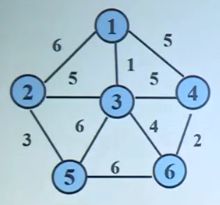
Prim算法是求解最小生成树的常用方法，它的思想非常简单，讲所有的点集合V分为 已经放入最小生成树集合的S和未放入的V-S，每次在V-S中选择一个距离S最近的点放入到S中，直到所有的点都放入S。就是很简单的贪心策略，不过可以证明是全局最优，prim算法对于稠密图效果比较好，具体步骤可以看点击打开链接，讲解的很清楚。

对于上面的图，显然最小生成树的结果应该是{1,3,6,2,4,5}或者{1,3,6,4,2,5}

#include 
#include

using namespace std;

#define MAX_INT 999999
pair GetShortestEdge(const vector >& Graph, const vector& isIncluded )//求当前在MST之外距离MST最近的点的id
{
    int minID = -1;
    int minDist = MAX_INT;
    pair minEdge;
    for(int i = 0; i < Graph.size(); i++)//i为MST内的点
    {
        if(!isIncluded[i]) continue;//如果不在MST里面，则跳过
        for(int j = 0; j < Graph.size(); j++) //j为MST外的点
            if(!isIncluded[j] && Graph[i][j] < minDist){ //找到不在MST内但是距离MST最近的点
                minID = j;
                minDist = Graph[i][j];
                minEdge = make_pair(i,j);
            }
    }
    return minEdge;

}

vector > Prim(const vector >& Graph, vector& isIncluded){
    vector > MST;
    isIncluded[0] = true;
    //MST.push_back();
    for(int i = 1; i < Graph.size(); i++){
        pair minEdge = GetShortestEdge(Graph, isIncluded); //找到这次要放入的边i，j
        MST.push_back(minEdge); //放入
        isIncluded[minEdge.second] = true; //将j标记为已经放入
    }
    return MST;
}

void addEdge( const int& startP, const int& endP, const int& weight ,vector >& Graph)
{
    Graph[startP][endP] = weight;
    Graph[endP][startP] = weight;
}

int main()
{
    int vertex_num = 6;
    vector > Graph(vertex_num, vector(vertex_num, MAX_INT));
    addEdge(0,1,6 ,Graph);
    addEdge(0,2,1 ,Graph);
    addEdge(0,3,5 ,Graph);
    addEdge(1,2,5 ,Graph);
    addEdge(1,4,3 ,Graph);
    addEdge(2,3,5 ,Graph);
    addEdge(2,4,6 ,Graph);
    addEdge(2,5,4,Graph);
    addEdge(3,5,2,Graph);
    addEdge(4,5,6,Graph);
    vector isIncluded(vertex_num, false);
    vector >  MST = Prim(Graph, isIncluded);
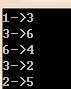
    for(int i = 0; i < MST.size(); i++) //按照放入MST的顺序依次输出
        cout << MST[i].first+1 << "->" << MST[i].second+1 << endl;

    return 0;
}

结果如下