TensorRT下FP32转INT8的过程

1. 关于TensorRT

      NVIDIA TensorRT是一种高性能神经网络推理(Inference)引擎，用于在生产环境中部署深度学习应用程序，应用有图像分类、分割和目标检测等，可提供最大的推理吞吐量和效率。TensorRT是第一款可编程推理加速器，能加速现有和未来的网络架构。TensorRT需要CUDA的支持。TensorRT包含一个为优化生产环境中部署的深度学习模型而创建的库，可获取经过训练的神经网络(通常使用32位或16位数据)，并针对降低精度的INT8运算来优化这些网络。借助CUDA的可编程性，TensorRT将能够加速助推深度神经网络日益多样化、复杂的增长趋势。通过TensorRT的大幅度加速，服务提供商能够以经济实惠的成本部署这些计算密集型人工智能工作负载。

 

 

2.关于int8 inference

对于INT8 推断（Inference），需要生成一个校准表来量化模型。接下来主要关注INT8推断（Inference）的几个方面，即：如何生成校准表，如何使用校准表，和INT8推断（Inference）实例。

 

1) 如何生成校准表？

校准表的生成需要输入有代表性的数据集， 对于分类任务TensorRT建议输入五百张到一千张有代表性的图片，最好每个类都要包括。生成校准表分为两步：第一步是将输入的数据集转换成batch文件；第二步是将转换好的batch文件喂到TensorRT中来生成基于数据集的校准表，可以去统计每一层的情况。

 

2) 如何使用校准表？

校准这个过程如果要跑一千次是很昂贵的，所以TensorRT支持将其存入文档，后期使用可以从文档加载，其中存储和加载的功能通过两个方法来支持，即writeCalibrationCache和readCalibrationCache。最简单的实现是从write()和read()返回值，这样就必须每次执行都做一次校准。如果想要存储校准时间，需要实现用户自定义的write/read方法，具体的实现可以参考TensorRT中的simpleINT8实例。

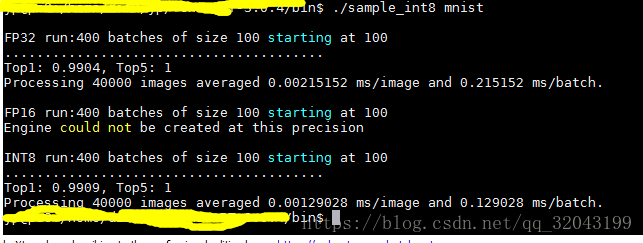
下图是simple_int8 mnist实例

下面我将介绍一下tensorrt的int8 inference的方法

3.tensorrt的int8 inference基本介绍

• 目标: 在没有明显准确度丢失的情况下将FP32的CNNs网络转换为INT8
• 理由: INT8类型的存储方式有很高的通量和较低的内存需求
• 挑战: 相对于FP32, INT8有明显较低的精度和动态范围
• 解决方式: 在将权值以及计算时最小化有效信息损失.
• 结果: 上述转换可以通过TensorRT来进行实现，同时该方法不需要额外的大量调整和重新训练.

4. 面临的挑战

• 相对于FP32，INT8的精度和动态范围要小很多：

• 从FP32到INT8需要不止一次的类型转换

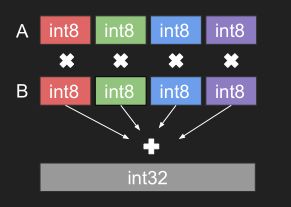
5. int8 类型的计算方式为何具有高通量

• 需要sm_61+ (Pascal TitanX, GTX 1080, Tesla P4, P40 and others)
• 四位字节积在32位结果中

计算方法： Result += A[0] * B[0] +A[1] * B[1] +A[2] * B[2] +A[3] * B[3]

我们必须保证没有精度损失和解决方案简单并且计算效率高

6.计算方法

6.1 线性量化法：

表现为：             Tensor Values = FP32 scale factor * int8 array + FP32 bias

实际上我们并不需要FP32 bias

所以：Tensor Values = FP32 scale factor * int8 array，即A = scale_A * QA

其中FP32 scale factor是一个浮点型的缩减系数，它随着优化过程改变 int8 array为一个int8型的矩阵

6.2 如何获得FP32 scale factor

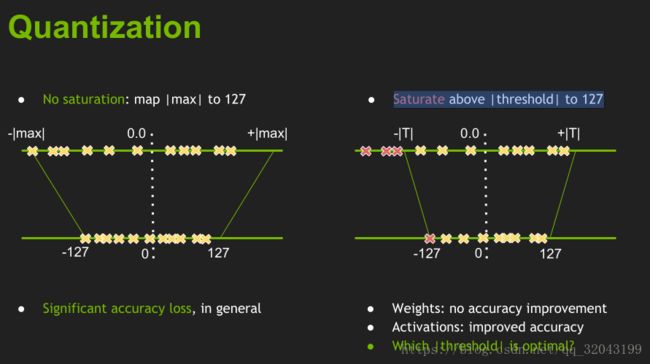
• 量化:

可见：它分为了两种情况，饱和与不饱和

不饱和我们可以将它全部映射到int8的精度上，但是过饱和时就需要设置阈值（saturate）

那我们如何去优化阈值的选择呢？

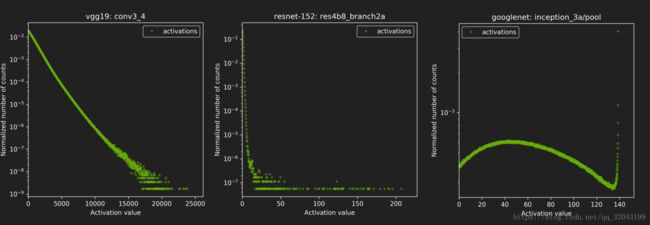
最小化信息丢失，因为FP32～int8只是重新编码信息。我们选择阈值时应尽量保证信息少丢失就行。下图是几种随着阈值变化而归一化数据指数变化的趋势（针对不同的模型，不同的layer，这个指数是不一样的）

我们用两种编码的相对熵来表示这个映射过程的好坏。

信息损失由Kullback-Leibler divergence (AKA relative entropy or information divergence)来衡量

• P, Q -两个离散概率分布
• KL_divergence(P,Q):= SUM(P[i] * log(P[i] / Q[i] ), i)

KL_divergence(P,Q)是判断映射的好坏，但如何进行映射呢，这里使用的是一个Calibration（校准器）或者说一个calibration dataset（矫正数据集）

过程如下：

• 在校准数据集上运行FP32推断。
• 对每一层

         1） 收集激活的直方图。

        2）  基于不同的饱和度阈值，生成多个量化分布

         3）  取最小阈值的量化

其实上面说起来基本思路是首先构建一种FP32数据向INT8数据的映射关系，该映射中的边界并不是两种数据类型的最大值，而是将FP32设置成一个Threshold，将这个阈值与INT8的最大值(127)构建映射关系，具体实现形式是通过一个scale来进行对应。

首先的问题是，这种映射关系的阈值如何寻找呢？不同的网路显然这一阈值是不同的，因此我们需要一个矫正数据集(calibration dataset)来进行scale的选取，其选择的标准为最小化KL_divergence(: KL_divergence(P,Q):= SUM(P[i] * log(P[i] / Q[i] ), i))

tensorrt上int8的工作流程;

你需要准备：

• 一个已经训练好的FP32的model
• 校准器（Calibration dataset.）

TensorRT将会：

• 在FP32上对校准数据集进行运行推断
• 收集需要的数据(不同阈值下的KL量化分布图)
• 运行矫正算法–> 优化scale系数
• 量化FP32权值到INT8
• 产生CalibrationTable和INT8 execution engine

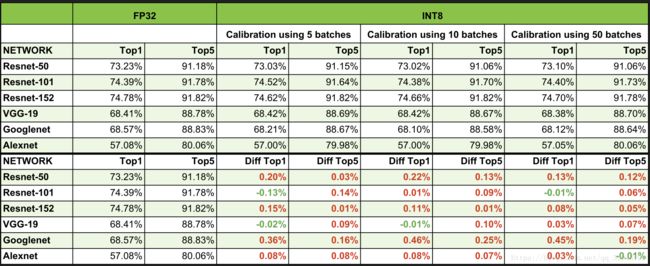
7. int8的效果

它能更高效的完成inference，且没有大的性能损失

8. 补充、

8.1 熵校准的伪码：

Input: FP32 histogram H with 2048 bins: bin[ 0 ], …, bin[ 2047 ]
For i in range( 128 , 2048 ):
reference_distribution_P = [ bin[ 0 ] , ..., bin[ i-1 ] ] // take first ‘ i ‘ bins from H
outliers_count = sum( bin[ i ] , bin[ i+1 ] , … , bin[ 2047 ] )
reference_distribution_P[ i-1 ] += outliers_count
P /= sum(P) // normalize distribution P
candidate_distribution_Q = quantize [ bin[ 0 ], …, bin[ i-1 ] ] into 128 levels 
                                               // explained later
expand candidate_distribution_Q to ‘ i ’ bins // explained later
Q /= sum(Q) // normalize distribution Q
divergence[ i ] = KL_divergence( reference_distribution_P, candidate_distribution_Q)
End For
Find index ‘m’ for which divergence[ m ] is minimal
threshold = ( m + 0.5 ) * ( width of a bin )


/*● KL_divergence(P, Q) requires that len(P) == len(Q)
● Candidate distribution Q is generated after merging ‘ i ’ bins from bin[0] to
bin[i-1] into 128 bins
● Afterwards Q has to be ‘expanded’ again into ‘i’ bins
Here is a simple example: reference distribution P consisting of 8 bins, we want to quantize into 2 bins:
P = [ 1, 0, 2, 3, 5, 3, 1, 7]
we merge into 2 bins (8 / 2 = 4 consecutive bins are merged into one bin)
[1 + 0 + 2 + 3 , 5 + 3 + 1 + 7] = [6, 16]
then proportionally expand back to 8 bins, we preserve empty bins from the original distribution P:
Q = [ 6/3, 0, 6/3, 6/3, 16/4, 16/4, 16/4, 16/4] = [ 2, 0, 2, 2, 4, 4, 4, 4]
now we should normalize both distributions, after that we can compute KL_divergence
P /= sum(P) Q /= sum(Q)
result = KL_divergence(P, Q)*/

8.2 int8 卷积核的伪码：

// I8 input tensors: I8_input, I8_weights, I8 output tensors: I8_output
// F32 bias (original bias from the F32 model)
// F32 scaling factors: input_scale, output_scale, weights_scale[K]
I32_gemm_out = I8_input * I8_weights // Compute INT8 GEMM (DP4A)
F32_gemm_out = (float)I32_gemm_out // Cast I32 GEMM output to F32 float
// At this point we have F32_gemm_out which is scaled by ( input_scale * weights_scale[K] ),
// but to store the final result in int8 we need to have scale equal to "output_scale", so we have to rescale:
// (this multiplication is done in F32, *_gemm_out arrays are in NCHW format)
For i in 0, ... K-1:
rescaled_F32_gemm_out[ :, i, :, :] = F32_gemm_out[ :, i, :, :] * [ output_scale / (input_scale * weights_scale[ i ] ) ]
// Add bias, to perform addition we have to rescale original F32 bias so that it's scaled with "output_scale"
rescaled_F32_gemm_out _with_bias = rescaled_F32_gemm_out + output_scale * bias
// Perform ReLU (in F32)
F32_result = ReLU(rescaled_F32_gemm_out _with_bias)
// Convert to INT8 and save to global
I8_output = Saturate( Round_to_nearest_integer( F32_result ) )

end！