论文:FCOS: Fully Convolutional One-Stage Object Detection
转载自大佬文章,有一点没看懂,还需要慢慢消化!
论文地址 | https://arxiv.org/pdf/1904.01355.pdf
1 .网络整体介绍
本文提出了一种全卷积one-stage目标检测算法(FCOS),以逐像素预测的方式解决目标检测问题,类似于语义分割。目前最流行的不论是one-stage目标检测算法,如RetinaNet,SSD,YOLOv3,还是two-stage目标检测算法,如Faster R-CNN。这两类算法大都依赖于预定义的锚框(anchor boxes)。相比之下,本文提出的目标检测算法FCOS不需要锚框。通过消除预定义的锚框,FCOS避免了与锚框相关的复杂计算,例如在训练期间计算重叠等,并且显著减少了训练内存。更重要的是,FCOS还避免了设定与锚框相关的所有超参数,这些参数通常对最终检测性能非常敏感。FCOS算法凭借唯一的后处理:非极大值抑制(NMS),实现了优于以前基于锚框的one-stage检测算法的效果。
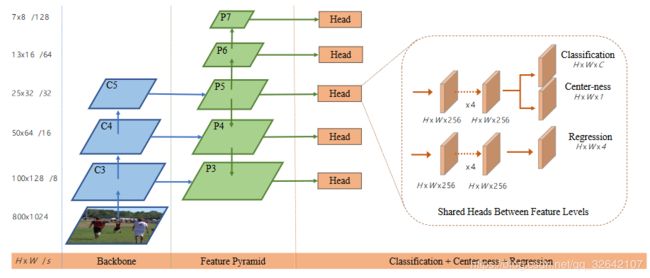
其实最著名的无anchor的目标检测网络是YOLOv1算法,YOLOv1算法纯粹是为了告诉大家,回归网络也可以进行目标检测,该网络由于其召回率过低而使其并无太多实用价值,因此YOLO作者在其基础上提出了基于anchor的YOLOv2算法。而本文提出的FCOS算法相当于保留了无anchor机制,并且引入了逐像素回归预测,多尺度特征以及center-ness三种策略,主要流程框架如下图所示,最终实现了在无anchor的情况下效果能够比肩各类主流基于anchor的目标检测算法。
2 .逐像素回归预测
YOLOv1中也使用了无anchor策略,但基于YOLOv1在预测边界框的过程中,提出的cell概念,导致YOLOv1只预测了目标物体中心点附近的点的边界框。这很显然预测的框少,召回率自然也就低了。基于此,本文提出的FCOS算法为了提升召回率,则对目标物体框中的所有点都进行边界框预测。当然这种逐像素的边界框预测肯定会导致最终预测得到的边界框质量不高,因此作者在后续还会提出弥补策略。
FCOS目标检测算法在边界框预测中使用的策略和YOLOv1有所不同,本文提出的预测策略如下:
如上两张图所示,FCOS算法在对目标物体框中所有的点进行目标框回归时,是用的距离各个边的长度的。之所以使用这种策略,而不使用主流目标检测算法的策略,其主要原因是为了后续使用center-ness做准备的。
由于FCOS算法是基于目标物体框中的点进行逐像素回归的,因此执行回归的目标都是正样本,所以作者使用了exp()函数将回归目标进行拉伸,我个人认为此操作是为了最终的特征空间更大,辨识度更强。最后,逐像素回归预测除了能够带来更多的框以外,更重要的是利用了尽可能多的前景样本来训练回归器,而传统的基于anchor的检测器,只考虑具有足够高的IOU的anchor box作为正样本。作者认为,这可能是FCOS优于基于anchor的同类检测器的原因之一。
3 .多尺度策略
对于基于anchor的检测算法,由于较大的降采样操作而导致的低召回率可以通过降低正anchor所需的IOU阈值做一定程度上的补偿,进行召回率的提升。然而对于FCOS算法,如果降采样的尺度过大,那么网络不可能回忆起一个在最终特征图上没有位置编码的对象的初始框的,基于此作者提出了基于FPN的多尺度策略。(虽然作者在文中说,即使没有FPN策略,逐像素检测网络在召回率上表现的也不逊色基于anchor的网络)
如上图所示,FCOS算法那使用了{P3, P4, P5, P6, P7}这五个尺度的特征映射。其中P3、P4、P5由主干CNNs网络的特征层 C3、C4、C5经过一个1*1的卷积得到的,而,P6、P7则是接着P5进行了步长为2的卷积操作得到的(相当于降采样,看注解)。最终对这五个尺度都做逐像素回归。
当然,本文为了能够更好的利用这种多尺度特征,在每一个尺度的特征层都限定了边界框回归的范围,不让其野蛮生长。(基于anchor的检测网络也有类似策略,比如YOLOv3中将不同大小的anchor分配到不同特征层级中作回归)更具体地说,作者首先计算所有特征层上每个位置的回归目标
-
第一:计算当前层级中的回归目标:l、t、r、b。
-
第二:判断max(l, t, r, b) > mi 或者 max(l, t, r, b) < mi -1是否满足。
-
第三:若满足,则不对此边界框进行回归预测。
-
第四:mi是作为当前尺度特征层的最大回归距离。
而且这种约束带来的额外的效果在于,由于不同尺寸的物体被分配到不同的特征层进行回归,又由于大部分重叠发生在尺寸相差较大的物体之间,因此多尺度预测可以在很大程度上缓解目标框重叠情况下的预测性能。
NOTE:: 由于作者认为,不同的特征层需要回归不同的尺寸范围(例如,P3的尺寸范围为[0,64],P4的尺寸范围为[64,128],因此在不同的特征层使用相同的输出激活是不合理的。因此,作者没有使用标准的exp(x)函数,而是使用exp(si,x)其中si是一个可训练的标量si,能够通过si来自动调整不同层级特征的指数函数的基数,这从经验上提高了检测性能。
4 .center-ness
由于FCOS算法使用了逐像素回归策略,在提升召回率的同时,会产生许多低质量的中心点偏移较多的预测边界框。基于此,作者提出了一个简单而有效的策略center-ness来抑制这些低质量检测到的边界框,且该策略不引入任何超参数。
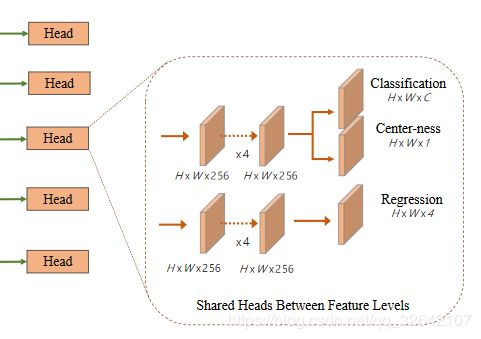
如上图所示,center-ness策略在每一个层级预测中添加了一个分支,该分支与分类并行,相当于给网络添加了一个损失,而该损失保证了预测的边界框尽可能的靠近中心。该损失的公式如下,其中l,r,t,b表示的为如下图左图中所示的预测值。
而该策略之所以能够有效,主要是在训练的过程中我们会约束上述公式中的值,使得其接近于0,这就导致如下图右图中的蓝色框中的短边能够向黄边靠近,使得分布在目标位置边缘的低质量框能够尽可能的靠近中心。这样的话,在最终使用该网络的过程中,非极大值抑制(NMS)就可以滤除这些低质量的边界框,提高检测性能。
5 .网络效果展示
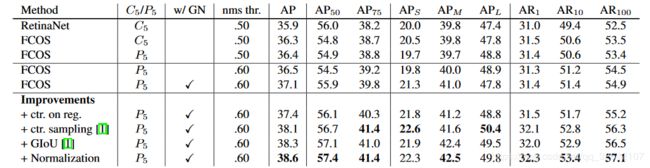
FCOS与其他最先进的two-stage或one-stage目标检测算法的比较。在相同主干网络的情况下,FCOS的性能比基于anchor的RetinaNet高出1.9%。FCOS的性能也优于最近推出的无anchor的one-stage检测网络CornerNet,且设计复杂度大大降低。(最后补一句,这种逐像素的策略,速度之所以没提,大家心知肚明哈!)