【神经网络】线性模型非线性模型,感知机与神经网络
刚才突然有一点懵。。神经网络的非线性到底体现在哪里?结合感知机为什么是线性模型思考了一下。
即使自我感觉已经把神经网络的结构搞的很透彻了,但是时不时得多问问自己还是可以发现新的问题。
线性模型和非线性模型区别
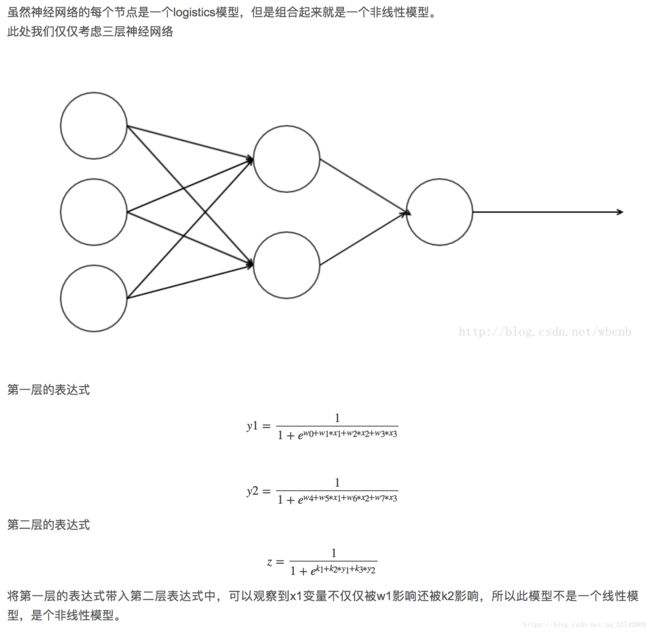
- 线性模型可以是用曲线拟合样本,但是分类的决策边界一定是直线的,例如logistics模型
- 区分是否为线性模型,主要是看一个乘法式子中自变量x前的系数w,如果w只影响一个x,那么此模型为线性模型。或者判断决策边界是否是线性的

- 其实最简单判别一个模型是否为线性的,只需要判别决策边界是否是直线,也就是是否能用一条直线来划分
感知机
什么是感知机模型呢,简而言之就是可以将有两个特征的数据集中的正例和反例完全分开的关于一条直线的函数,或者可以是关于三维空间中的一个平面的函数,更可以是关于高维的一个超平面的函数。
图即为感知机的模型,仔细一看就会发现,其实就是一个单层的神经网络,激活函数是跃阶函数。
从这个式子很容易就看出来,每个w只影响一个x,所以感知机是一个经典的线性模型,只能够处理线性可分的问题。
具体的感知机算法不是本文的重点。
神经网络
神经网络是非线性
简单明了,就可以看出神经网络是非线性的了。
但其实一开始困扰了我的是另一个问题。
在Yjango大神的超智能体中,有写到
激活函数确实可以产生非线性的变换,但对于神经网络模型而言,整个处理非线性可分的能力关键不在于激活函数,而是神经网络之间的多层叠加,使得只能处理线性可分问题的感知机(神经元)可以处理非线性可分问题。
但激活函数同样是必不可少的。如果神经网络中的神经元都不带激活函数,那么神经元无论怎么样堆叠,都只能够处理线性问题。为什么必不可少可以看这篇文章:激活函数的作用
虽然没有激活函数时,每个变量也被多个权值所影响,但不同的是,此时每个变量都以独立于其它变量区分开来。
而当引入非线性的激活函数时,每个变量是无法与其它变量所独立开来的!
在二维空间中,无论用多么复杂的激活函数,决策平面依旧是线性的。那激活函数在干嘛?好,来回顾一张图
为什么同样是sigmoid,LR是线性,神经网络是非线性,之前有解释过。但可能从理论上理解了,但是直观来想,可能还不清楚。LR的sigmoid函数切了一刀,这一刀就是判决平面(下图中的白色线条),空间被映射成一个坡状(这里体现了一部分的“弯曲”)。但对于LR而言,它拿走了判决平面就不管了,而神经网络将这些坡组合起来,也就是利用了sigmoid函数的输出。从而形成了最右图的白色圆圈。
这是tensorflow playground中的运行实例,注意看每个神经元的颜色分割。
这部分不是我们研究的重点,这只是给定神经网络的输入特征,一般信息越多越容易分开。
重点看这两部分,每个神经元都会有一条切割线。这也暗含了之前讲的感知机是线性模型的道理。因为每个神经元其本质上就是一个感知机。而激活函数在这边做了一件什么事情。就是越复杂的激活函数其在单个神经元上的线性可分能力就越强!有一个想都不要想的道理,每个神经元的分类能力越强,那整体的神经网络的性能肯定越优秀。
到这里可以总结一下,激活函数的功能就在于使得单个神经元具有更强大的分割能力,每个神经元就是切一刀,合适的激活函数,可以让这一刀切的很准。
再将新的特征经由神经网络堆叠,所有的特征基本上就都混在一起了。继续观察上图,第二层第一个神经元是怎么来的,就是之前的四个神经元堆叠产生的。你可以这么想,蓝色的是高的地方,黄色的是低的地方。四个神经元叠在一起,本来是类似于阶梯状的,但是由于四个阶梯的中间都是高的,周围都不全是高,有高有低,所以最后就形成了中间高四周低的形状。然后神经元的作用依旧是切一刀,把山头给切了下来。就是
这个形状了。
但事实上,弯曲这件事不好说是不是真的弯曲,只是不断映射到高维空间,将样本稀疏化,然后不断去寻找一个线性可分的超平面将样本分离开来(注意是线性可分,每个神经元都只是切一刀)。“弯曲”的含义在我们直观上来理解是被扭曲了,其实也确实是这么回事,从样本分布上来理解,就是正的样本都被拉到一头,负的样本被拉到另一头,变成一座山的样子。
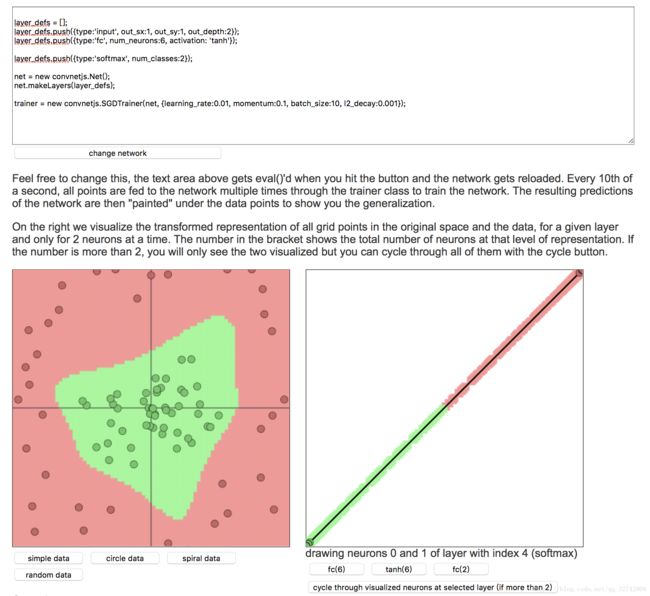
下面来个实例,有个网站很好的https://cs.stanford.edu/people/karpathy/convnetjs//demo/classify2d.html
还是类似于刚才那个形状,这里只有一个输入层,一个隐含层,一个softmax输出层。激活函数一共有两个,但实际上只是被扭曲了一次,只被堆叠了一次。就像刚才我描述的,中间的样本往山头去,四周的样本网山脚去。
右边的图只是把图像二维化了,把一座山变成了一条线。
总结一下
激活函数越复杂单个神经元切一刀的能力就越强,切的越准。
神经网络的非线性能力体现在激活函数上。堆的越深,样本在映射空间中的分布就越稀疏,分布一稀疏,判决超平面就好找,切一刀也好切。就像上面的例子,将样本稀疏分布到山头和山脚,在山腰上切一刀就完全分开了。
神经网络还有不少东西可以研究。就上图那个网站的可视化分布就是一个很好的学习的例子。话说斯坦福是真的厉害,能作出这种demo来,那个理解深度想必是真正的吃透了。
参考文章:
线性模型与非线性模型:https://blog.csdn.net/wbcnb/article/details/78306970
感知机原理:https://www.cnblogs.com/pinard/p/6042320.html