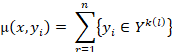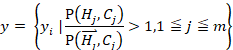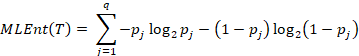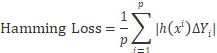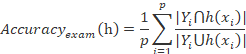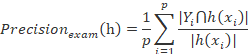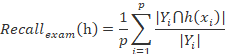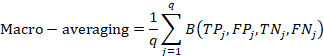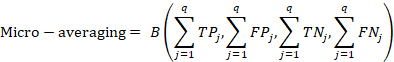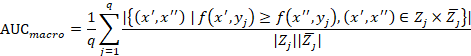多标签分类
1、多标签分类 VS 单标签分类
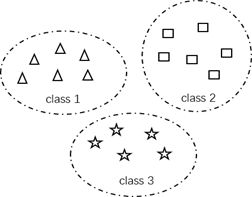
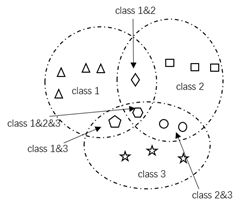
在图像的分类和识别领域,传统的单标签分类旨在解决一个示例只属于一个类别的问题,不同的标签之间完全独立、互相之间没有关联。然而,在更加复杂的分类任务中,如文本分类、图像类别标注、语义场景分类等一些实际应用中,常常会出现一个示例同时属于多个类别(比如:一张电影海报图片可能会同时有科幻、动作、喜剧等多个标签),下图展示了单标签分类和多标签分类之间的区别。
在实际多标签分类问题中,标签之间并非完全独立,标签之间存在一定的依赖关系或者互斥关系。但由于多标签分类任务往往涉及的标签数量较大,导致类别之间的依赖关系较为复杂,难以找到合理的方式对其进行描述。因此,多标签分类相对于传统的单标签分类任务而言更加复杂,难以分析。
2、多标签分类算法
参考论文:A Review On Multi-Label Learning Algorithms
多标签分类的输出空间会随着标签的数量指数增长,为了应对指数复杂度的标签空间,需要挖掘标签之间的相关性。有效的挖掘标签之间的相关性,是多标签学习成功的关键。根据多标签分类算法所利用的标签相关性情况,分为一阶、二阶、高阶策略分类算法。
a) 一阶策略(First-order strategy)
忽略和其他标签的相关性,比如把多标签分类分解为多个独立的二分类问题。 一阶策略的显著优点在于其概念简单、效率高。另一方面,由于其忽略了标签相关性,多标签分类算法的性能可能较差。
b) 二阶策略(Second-order strategy)
考虑标签之间的成对关联关系,比如为相关标签和不相关标签排序。由于二阶策略一定程度上利用了标签相关性,因此,基于二阶策略的多标签分类算法可以获得较好的泛化性能。然而,在实际的应用当中,标签相关性一般超出了二阶相关。
c) 高阶策略(High-order strategy)
考虑多个标签之间的关联,比如对每个标签考虑所有其他标签的影响。显然,高阶策略比一阶策略和二阶策略具有更强的相关性建模能力,而另一方面,高阶策略在计算上要求更高。
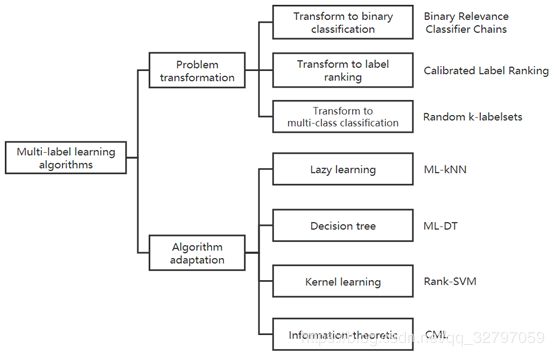
如果根据算法设计思想的来源,可以将多标签分类算法分为两类:问题转换的方法和算法改编的方法。如下图所示,基于问题转换的多标签分类方法一般将多标签分类问题转换为其他学习场景,比如转换为二分类问题、标签排序问题、多分类问题等。基于算法改编的多标签分类方法一般是通过改编流行的学习算法去直接处理多标签数据,比如改编决策树、支持向量机等等,随着近些年深度学习的发展,部分学者将CNN、RNN等深度学习算法进行改编,常常是修改多分类神经网络的输出层或者将多种模型并联使用,使其适用于多标签的分类,下面将对部分算法进行简要介绍。
1、问题转换方法
a)Binary Relevance
将多标签分类问题转换为二分类问题,将标签分类开来针对N个标签建立N个二分类器对每个标签进行预测,这是最为简单直接的方法,没有考虑标签之间的关联性,是一阶策略分类算法。
b)Calibrated Label Ranking
将多标签分类问题转换为标签排序问题,对于N个标签,构建N(N-1)/2个标签对,为每个标签对![]() 构建二分类器时,将属于标签
构建二分类器时,将属于标签![]() 但不属于标签
但不属于标签![]() 的样本看作是正类样本,将属于标签
的样本看作是正类样本,将属于标签![]() 但不属于标签
但不属于标签![]() 的样本看作是负类样本,忽略其他样本,可以构建N(N-1)/2个数据集,用每一个数据集训练一个二分类器,给定一个测试样本,当分类器的返回值大于零时,样本属于标签
的样本看作是负类样本,忽略其他样本,可以构建N(N-1)/2个数据集,用每一个数据集训练一个二分类器,给定一个测试样本,当分类器的返回值大于零时,样本属于标签![]() ,否则属于标签
,否则属于标签![]() ,对每个二分类器的预测值进行投票,对每个标签添加一个额外的虚拟标记
,对每个二分类器的预测值进行投票,对每个标签添加一个额外的虚拟标记![]() ,将其作为测试样本与每个标签的相关与不相关的一个划分点,将排序后的投票结果划分为该样本的相关标签和不相关标签。最终不仅给出样本所属标签集合,还根据标签与样本的相关程度给出类别标签的顺序。该算法只考虑两个标签之间的关联,是二阶策略。
,将其作为测试样本与每个标签的相关与不相关的一个划分点,将排序后的投票结果划分为该样本的相关标签和不相关标签。最终不仅给出样本所属标签集合,还根据标签与样本的相关程度给出类别标签的顺序。该算法只考虑两个标签之间的关联,是二阶策略。
c)Random k-labelsets
将多标签分类问题转换为多分类问题。把![]() 个可能的标签对,映射成
个可能的标签对,映射成![]() 个自然数。其映射函数记为
个自然数。其映射函数记为![]() ,则原数据集变为:
,则原数据集变为:
![]()
根据新构建的数据集训练一个多分类器,给定一个测试样本后,多分类器输出一个自然数,根据输出的自然数映射回标签集,该算法被称为LP(Label Powerest)算法,该算法有两个主要的局限性:
- 预测的标签集是训练集中已经出现的,无法泛化到未见过的标签集
- 当标签数量较大时,该算法较为低效
为了克服LP算法的局限性,Random k-labelsets算法使用LP分类器只训练Y中一个长度为k的子集,然后集成大量的LP分类器来预测。![]() 表示Y的所有的长度为k的子集,
表示Y的所有的长度为k的子集,![]() 表示随机取的一个长度为k的子集,这样就可以进行收缩样本空间,得到如下样本集和标签集:
表示随机取的一个长度为k的子集,这样就可以进行收缩样本空间,得到如下样本集和标签集:
![]()
![]()
随机选取n个子集:![]() 来构造n个多分类器做集成使用。在预测阶段计算两个指标,标签j的最大投票数,实际投票数,对未知样本进行预测时,以0.5为阈值进行预测,得到标签集。
来构造n个多分类器做集成使用。在预测阶段计算两个指标,标签j的最大投票数,实际投票数,对未知样本进行预测时,以0.5为阈值进行预测,得到标签集。
因为对多标签分类器进行训练时,所使用的训练集是随机长度为k的子集,考虑了多个标签之间的相关性,是高阶策略。
2、算法改编方法
a)Multi-Label k-Nearest Neighbor(ML-KNN)
该算法是一种懒惰的多标签分类算法,是由传统的k近邻算法衍生出来的。对于每个测试样本,用![]() 表示测试样本x的k个近邻样本,用表示样本x的邻居中带有标签
表示测试样本x的k个近邻样本,用表示样本x的邻居中带有标签![]() 的个数。用
的个数。用![]() 表示样本x含有标签
表示样本x含有标签![]() ,根据后验概率最大化的规则,有
,根据后验概率最大化的规则,有
该算法没有考虑标签之间的相关性,是一阶策略。
b)Multi-Label Decision Tree(ML-DT)
使用决策树的思想来处理多标签分类问题在数据集T中,使用第i个标签,划分值为δ,计算出如下信息增益:
![]()
![]()
递归的构建一棵决策树每次选取标签和划分值,使得上式的信息增益最大,其中熵可以按照如下方式进行计算:
其中,![]() 表示标签
表示标签![]() 在样本集T中的分数,对未知样本进行测试时,向下遍历决策树,找到叶子节点,若
在样本集T中的分数,对未知样本进行测试时,向下遍历决策树,找到叶子节点,若![]() 大于0.5,则表示含有标签
大于0.5,则表示含有标签![]() ,该算法没有考虑标签之间的相关性,是一阶策略。
,该算法没有考虑标签之间的相关性,是一阶策略。
c)CNN-RNN
参考文献:CNN-RNN: A Unified Framework for Multi-label Image Classification
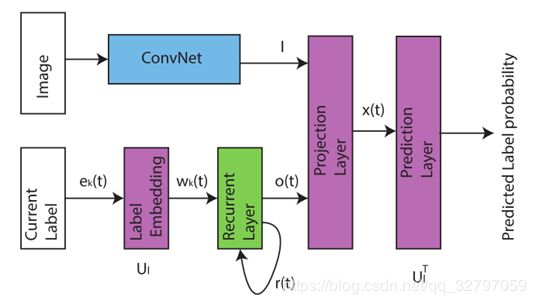
使用深度学习思想来解决多标签分类问题,如下图所示将CNN与RNN并联使用。
在该模型中,CNN部分用于提取图像的语义特征,RNN部分用于描述图像/标签关系,因为RNN可以通过中间状态保存上下文信息,作为输入影响下一时序的预测,所以在该模型中,RNN同时用于表示标签之间的依赖关系,是高阶策略。
将当前被预测标签通过独热编码进行表示,即标签k表示为![]() ,第k个位置为1,其余位置为0。标签嵌入矩阵为
,第k个位置为1,其余位置为0。标签嵌入矩阵为![]() ,嵌入矩阵的第k行为标签k的嵌入表示,获取标签k的嵌入表示:
,嵌入矩阵的第k行为标签k的嵌入表示,获取标签k的嵌入表示:
![]()
RNN部分内存有此前被预测标签的表示,结合当前输入的标签表示对标签相关性进行建模,RNN的状态更新如下,其中,![]() 为第t步时RNN的隐藏状态,
为第t步时RNN的隐藏状态,![]() 为第t步时RNN的输出。
为第t步时RNN的输出。
![]()
![]()
将RNN部分输出与CNN部分提取的图像语义特征共同映射到低维的特征嵌入空间,![]() 与
与![]() 为映射矩阵。
为映射矩阵。
![]()
通过计算![]() 与每个特征嵌入之间的距离来计算测试样本的标签得分,预测标签的概率可以使用softmax函数进行计算。
与每个特征嵌入之间的距离来计算测试样本的标签得分,预测标签的概率可以使用softmax函数进行计算。
![]()
![]()
使用交叉熵作为的模型损失函数,其中,p表示样本的真实标签分布,q表示预测标签的概率分布,交叉熵越小,两个概率分布越接近。
3、评价指标
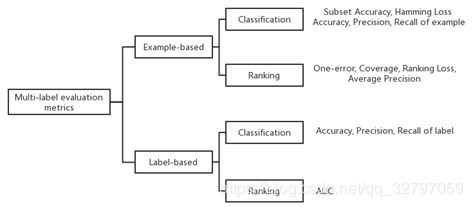
在多样本分类中,所使用的评价指标沿用了单标签分类的评价指标,对其做了部分修改以适用于多标签分类任务。如下图所示,可分为两类评价准则:基于样本的评价指标,基于标签的评价指标。
1、基于样本的评价指标
a)Subset Accuracy
该评价指标的衡量标准是被正确分类的样本所占的比例,预测的样本的标签集与真实的标签集完全一样算正确,该评价指标对于标签的准确度的要求较为严格,所以,多数的多标签分类算法在该指标下的性能较差,尤其是当标签空间较大时。
b)Hamming Loss
该评价指标的衡量标准是被错分的标签的比例,即正确标签没有被预测以及错误的标签被预测的占比,△表示两个集合之间的对称差分。
c)![]()
即单标签分类中的准确率,精确率,召回率,![]() 是精准率与召回率在平衡系数β(β>0)下的集成版本,当β=1时,
是精准率与召回率在平衡系数β(β>0)下的集成版本,当β=1时,![]() 是精准率与召回率的调和平均数。
是精准率与召回率的调和平均数。
d)Ranking Loss
该指标的评价标准是反序标签对的占比,即不相关标签比相关标签的相关性还大的情况,![]() 为标签集
为标签集![]() 的补集,
的补集,![]() 从标签集
从标签集![]() 中选取,
中选取,![]() 从标签集
从标签集![]() 中选取。值越小,分类器的表现越好。
中选取。值越小,分类器的表现越好。
2、基于标签的评价指标
a)Macro-averaging, Micro-averaging
对于多标签分类任务中的每个标签![]() ,定义表征二分类性能的四个基本量。
,定义表征二分类性能的四个基本量。
![]()
![]()
![]()
![]()
换而言之,![]() 表示标签
表示标签![]() 的真正例、假正例、真反例、假反例,且
的真正例、假正例、真反例、假反例,且![]() ,p为样本总数。Macro-averaging先对单个标签下的数量表征进行计算指标,然后再对多个标签取平均值。Micro-averaging先对多个标签的数量表征进行计算,再根据数量表征得到常规指标。
,p为样本总数。Macro-averaging先对单个标签下的数量表征进行计算指标,然后再对多个标签取平均值。Micro-averaging先对多个标签的数量表征进行计算,再根据数量表征得到常规指标。![]() 表示对四个表征进行相关运算得到常规的二分类指标。
表示对四个表征进行相关运算得到常规的二分类指标。
b)AUC
AUC所表示的是随机挑选一个正样本及一个负样本,根据当前分类器进行预测,正样本预测为正的概率值大于负样本预测为正的概率值。对于多标签分类而言,有两种计算方式。
![]()
![]()
![]()
![]()
4、存在的问题及挑战
1、分类算法的性能有待提高
现如今已有的多标签分类算法的分类性能仍有待提高,同时多标签分类的输出空间会随着样本关联到标签个数的增长呈现指数式增长,导致分类问题变得越来越复杂,导致模型的整体性能较差。近年来,部分学者将深度学习应用到了多标签分类任务中,虽然对于传统算法而言精确度有所提升,但是深度学习模型较为复杂,导致基于深度学习的多标签分类模型的分类效率较低。
2、标签之间的依赖关系难以描述
对于标签之间的依赖关系的描述有三种策略:1、一阶策略,忽略标签之间的相关性,比如把多标签分类分解为多个独立的二分类问题;2、二阶策略,只考虑标签之间的成对关联关系;3、高阶策略,考虑多个标签之间的关联关系。针对具体的应用场景,该采用哪种相关性建模策略仍然是一个未解决的问题且缺乏相应的指导依据。
3、多标签分类数据集存在类别不平衡问题
同时,多样本分类数据集中正样本/负样本数量可能远远少于负样本/正样本数量,即多标签分类中存在类的不平衡问题,该问题也是单标签分类中常见的问题,该问题会导致大多数多标签分类方法性能的下降。例如,在预测肺癌的场景中,肺癌患者在所有来诊病人中所占的比例非常低,该场景下如果直接构建模型,会导致数据集以负样本为主,有很少的正样本。由分类模型的目标是希望准确率尽可能达到最高,因此该场景问题最终会导致预测的结果全部偏向负样本,但在实际生活中,医生和病人更加关注肺癌患者的情况,对非肺癌患者的关注度并没有那么高,类不平衡问题会严重影响到分类的效果。
4、多标签分类数据集含噪声
现有的多标签分类数据集,多数是由人工进行标注的,在人工标注的过程中由于各种各样的原因如每个人对相同事务的不同理解,造成标签的错误标注或者丢失了部分标注,最终得到的数据标签是不准确的或者是带有噪声的。因此在实际应用中,有完整正确的已知标签的数据量是很有限的,但是标签错误或者丢失部分标签的数据却很多。因此,有必要对此类数据进行深入研究,充分挖掘其内在的结构并将其应用到分类模型的构造中,进而提高分类准确度。