TensorFlow入门(二):合成特征与离群值
简介
- TensorFlow入门(二):合成特征与离群值
- 1.模型目标
- 2.代码
TensorFlow入门(二):合成特征与离群值
1.模型目标
- 创建一个合成特征,即另外两个特征的比例
- 将此新特征用作线性回归模型的输入
- 通过识别和截取(移除)输入数据中的离群值来提高模型的有效性
由于本节中所用到的仍然是线性回归算法,所以大部分的代码都与上一节相同,不同的是我们需要定义一个全新的合成特征,这里选择通过房间数除以人口合成一个人均房间数特征,即如下所示:
california_housing_dataframe["rooms_per_person"] = (california_housing_dataframe["total_rooms"] / california_housing_dataframe["population"])
之后,我们通过一些方法来识别离群值,并用下面这个函数将rooms_per_person 的值截取为 5
california_housing_dataframe["rooms_per_person"]).apply(lambda x: min(x, 5))
2.代码
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import sklearn.metrics as metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
california_housing_dataframe = pd.read_csv(
"https://download.mlcc.google.cn/mledu-datasets/california_housing_train.csv", sep=",")
california_housing_dataframe = california_housing_dataframe.reindex(
np.random.permutation(california_housing_dataframe.index))
california_housing_dataframe["median_house_value"] /= 1000.0
print(california_housing_dataframe)
#-------- 定义输入函数 ----------#
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
# 这里得到的features是一个dict,具体为{'total_rooms': array([ 5039.,1840., ..., 705.])}
# 其仅有一对{key,value}值,这里的value实际上是一个array对象
features = {key: np.array(value) for key, value in dict(features).items()}
# 构造一个数据集
ds = Dataset.from_tensor_slices((features, targets))
ds = ds.batch(batch_size).repeat(num_epochs)
# 若shuffle为真,则对数据进行随机处理
if shuffle:
ds = ds.shuffle(buffer_size=10000)
# 返回下一批数据
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
#---------- 训练模型的函数,通过不同的参数调用来了解不同的效果 ------------
def train_model(learning_rate, steps, batch_size, input_feature):
"""Trains a linear regression model.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
input_feature: A `string` specifying a column from `california_housing_dataframe`
to use as input feature.
Returns:
A Pandas `DataFrame` containing targets and the corresponding predictions done
after training the model.
"""
periods = 10
steps_per_period = steps / periods
my_feature = input_feature
my_feature_data = california_housing_dataframe[[my_feature]].astype('float32')
my_label = "median_house_value"
targets = california_housing_dataframe[my_label].astype('float32')
# Create input functions.
training_input_fn = lambda: my_input_fn(my_feature_data, targets, batch_size=batch_size)
predict_training_input_fn = lambda: my_input_fn(my_feature_data, targets, num_epochs=1, shuffle=False)
# Create feature columns.
feature_columns = [tf.feature_column.numeric_column(my_feature)]
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# Set up to plot the state of our model's line each period.
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
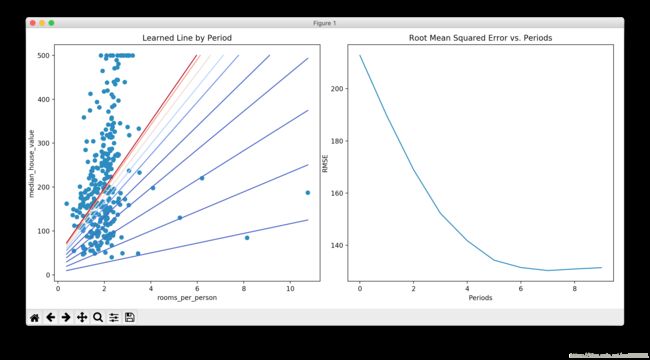
plt.title("Learned Line by Period")
plt.ylabel(my_label)
plt.xlabel(my_feature)
sample = california_housing_dataframe.sample(n=300)
plt.scatter(sample[my_feature], sample[my_label])
colors = [cm.coolwarm(x) for x in np.linspace(-1, 1, periods)]
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
root_mean_squared_errors = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period,
)
# Take a break and compute predictions.
predictions = linear_regressor.predict(input_fn=predict_training_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
# Compute loss.
root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(predictions, targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, root_mean_squared_error))
# Add the loss metrics from this period to our list.
root_mean_squared_errors.append(root_mean_squared_error)
# Finally, track the weights and biases over time.
# Apply some math to ensure that the data and line are plotted neatly.
y_extents = np.array([0, sample[my_label].max()])
weight = linear_regressor.get_variable_value('linear/linear_model/%s/weights' % input_feature)[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
x_extents = (y_extents - bias) / weight
x_extents = np.maximum(np.minimum(x_extents,
sample[my_feature].max()),
sample[my_feature].min())
y_extents = weight * x_extents + bias
plt.plot(x_extents, y_extents, color=colors[period])
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.subplot(1, 2, 2)
plt.ylabel('RMSE')
plt.xlabel('Periods')
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(root_mean_squared_errors)
plt.pause(0)
# Create a table with calibration data.
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
display.display(calibration_data.describe())
print("Final RMSE (on training data): %0.2f" % root_mean_squared_error)
return calibration_data
#---------- 函数结束 ------------
# 任务1:尝试合成特征(即total_rooms与population的比例)
california_housing_dataframe["rooms_per_person"] = (california_housing_dataframe[
"total_rooms"] / california_housing_dataframe["population"])
calibration_data = train_model(
learning_rate=0.05,
steps=500,
batch_size=5,
input_feature="rooms_per_person")
# 任务2:识别离群值
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.scatter(calibration_data["predictions"], calibration_data["targets"])
plt.subplot(1, 2, 2)
_ = california_housing_dataframe["rooms_per_person"].hist()
plt.pause(0)
# 任务3:截取离群值
california_housing_dataframe["rooms_per_person"] = (
california_housing_dataframe["rooms_per_person"]).apply(lambda x: min(x, 5))
_ = california_housing_dataframe["rooms_per_person"].hist()
plt.pause(0)
calibration_data = train_model(
learning_rate=0.05,
steps=500,
batch_size=5,
input_feature="rooms_per_person")