K近邻法(KNN)(学习笔记、C++代码实现)(未完持续更新)
K近邻法
参考:《统计学习方法-李航》
K近邻法(K-nearest neighbor,k-NN)是一种基本分类和回归方法,本文为分类方面的学习笔记。
K近邻法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别。
K值的选择、距离度量及分类决策规则是K近邻法的三个基本要素
K近邻算法
K近邻算法的基本思路:给定一个训练集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,则把输入实例分为这个类。
算法叙述
输入:训练数据集 = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } =\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} ={(x1,y1),(x2,y2),...,(xN,yN)}
其中, x i ∈ x ⊆ R n x_i \in x \subseteq R^n xi∈x⊆Rn为实例的特征向量, y i ∈ Y = { c 1 , c 2 , . . . , c k } y_i \in Y=\{ c_1,c_2,...,c_k \} yi∈Y={c1,c2,...,ck}为实例的类别,i=1,2,…,N;实例特征向量x;
输出:实例x所属的类y。
(1)根据给定的距离度量,在训练集T中找出与x最邻近的k个点,涵盖这k个点的x的领域基座 N k ( x ) N_k(x) Nk(x);
(2)在 N k ( x ) N_k(x) Nk(x)中根据分类决策规则(如多数表决)决定x的类别y:
y = a r g m a x ∑ x i ∈ N k ( x ) I ( y i = c j ) , i = 1 , 2 , . . , N ; j = 1 , 2 , . . . , K y=argmax \sum_{x_i \in N_k(x)}^{}I(y_i=c_j),i=1,2,..,N;j=1,2,...,K y=argmaxxi∈Nk(x)∑I(yi=cj),i=1,2,..,N;j=1,2,...,K
上式中,I为指示函数,即当 y i = c i y_i=c_i yi=ci时I为1,否则I为0.
K近邻模型
K近邻法使用的模型实际上对应于对特征空间的划分。模型由三个基本要素–距离度量、k值的选择和分类决策规则决定。
模型
k近邻法中,当训练集、距离度量(如欧氏距离)、k值、即分类决策规则(如多数表决)确定后,对于任何一个新的输入实力,它所属的类唯一地确定。
其中以K最近邻算法中可以清晰的看明白:
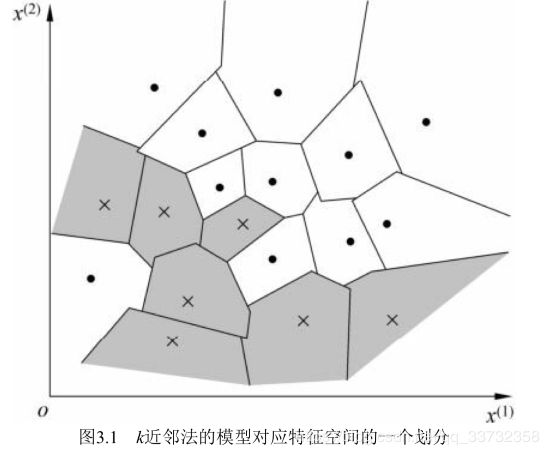
距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反应。
设特征空间x是n为实数向量空间 R n R^n Rn, x i , x j ∈ X , X i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T , X j = ( x j ( 1 ) , x j ( 2 ) , . . . , x j ( n ) ) T x_i,x_j\in X,X_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T,X_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T xi,xj∈X,Xi=(xi(1),xi(2),...,xi(n))T,Xj=(xj(1),xj(2),...,xj(n))T, x i , x j x_i,x_j xi,xj的 L p L_p Lp距离定义为
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) ( 1 / p ) L_p(x_i,x_j)=(\sum_{l=1}^{n}|x_i^{(l)}-x_j^{(l)}|^p)^{(1/p)} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)(1/p)
这里p>=1.当p=2时,称为欧氏距离;当p=1时,称为曼哈顿距离;当p=无穷大时,它是各个坐标距离的最大值。
明显的,不同的距离度量所确定的最近邻点是不同的。
k值的选择
k值的选择会对k近邻法的结果产生重大影响。
通常采用交叉验证法来选取最优的k值。
k值减小,近似误差减小,估计误差增大。模型变得复杂,易过拟合:
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大,预测结果会对近邻的实例点非常敏感。如果临近的实例点恰巧是噪声,预测就会出错。换句话说,k值的减小就意味着整体模型变得复杂,容易过拟合。
k值较大,模型变得简单,预测效果差:
如果选择较大的k值,就相当于用较大邻域中的训练实力进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这是与输入实例较远的(不相似)训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单。
注:
近似误差:
可以理解为对现有训练集的训练误差。近似误差关注训练集,如果近似误差小了会出现过拟合的现象,对现有的训练集能有很好的预测,但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。
估计误差:
可以理解为对测试集的测试误差。估计误差关注测试集,估计误差小了说明对未知数据的预测能力好。模型本身最接近最佳模型。
分类决策规则
k近邻法中的分类决策规则往往是对数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
k近邻法的实现:kd树
实现k近邻法主要考虑的问题使如何对训练数据进行快速k近邻搜索。这点在特征空间的维数大及训练数据容量大时尤其必要。
为了提高k近邻搜索的效率,使用特殊的结构存储训练数据,以减少计算距离的次数。其中以kd树方法最为广泛使用。
构造kd树
kd树的含义:
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树,表示对k维空间的一个划分。构造kd树相当于不断地用垂直与坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域。kd树的每个节点对应于一个k维超矩形区域。
构造kd树的方法:
构造根节点,使根节点对应于k维空间中包含所有实例点的超矩形区域;通过下面的递归方法,不断对k维空间进行切分,生成子节点。在超矩形区域(节点)上选择一个坐标轴和此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直与选定的坐标轴,将当前超矩形区域切分左右两个子区域(子节点);这时,实例被分到两个子区域。这个过程直道子区域没有实例时终止(终止时的结点维叶结点)。在此过程中,将实例保存在相应的结点上。
算法叙述
输入:k维空间数据集 T = { x 1 , x 2 , . . . , x N } T=\{x_1,x_2,...,x_N\} T={x1,x2,...,xN},其中 x i = ( x i 1 , x i 2 , . . . , x i k ) T , i = 1 , 1 , . . . , N x_i=(x_i^{1},x_i^{2},...,x_i^{k})^T,i=1,1,...,N xi=(xi1,xi2,...,xik)T,i=1,1,...,N;
输出:kd树。
(1)开始:构造根结点,根结点对应于包含T的k维空间的超矩形区域。选择 x ( 1 ) x^{(1)} x(1)为坐标轴,以T中所有实例的 x ( 1 ) x^{(1)} x(1)坐标的中位数为切分点,将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x ( 1 ) x^{(1)} x(1)垂直的超平面实现。
由分界点生成深度为1的左、右子结点:左子结点对应坐标 x ( 1 ) x^{(1)} x(1)小于切分点的子区域,右子结点对应于坐标 x ( 1 ) x^{(1)} x(1)大于切分点的子区域。
将落在切分超平面上的实例点保存在根结点。
(2)重复:对深度为j的结点,选择 x ( l ) x^{(l)} x(l)为切分的坐标轴,l=j(modk)+1,以该结点的区域中所有实例的 x ( l ) x^{(l)} x(l)坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域。切分右通过切分点并于坐标轴 x ( l ) x^{(l)} x(l)垂直的超平面实现。
由该结点生成深度为j+1的左、右子结点:左子结点对应坐标 x ( l ) x^{(l)} x(l)小于切分点的子区域,右子结点对应坐标 x ( l ) x^{(l)} x(l)大于切分点的子区域。
将落在切分超平面上的实例点保存在该节点。
(3)直道两个子区域没有实例存在时停止。从而形成kd树的区域划分。
例:
T = { ( 2 , 3 ) T , ( 5 , 4 ) T , ( 9 , 6 ) T , ( 4 , 7 ) T , ( 8 , 1 ) T , ( 7 , 2 ) T } T=\{(2,3)^T,(5,4)^T,(9,6)^T,(4,7)^T,(8,1)^T,(7,2)^T\} T={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}

更新标签:2019年4月6日13点17分
C++实现
Step1:选择判定维度axis_index;
Step2:根据axis_index排序输入空间;
Step3:选择中分点作为子KD树的根结点作为上层父结点的孩子(左/右)(当然总KD树的根结点不需要链接上层结点),并切分输入空间为左输入空间和右输入空间,传入Step1递归进行直到输入空间都为空。
#pragma once
#include
#include
#include
#include
using namespace std;
struct Node
{
vector *data;
int split;
Node *left;
Node *right;
Node(vector *data_) {
data = data_;
split = 0;
left = NULL;
right = NULL;
}
};
class KDTree
{
private:
Node* root;
public:
vector> data = { {1,1,1},
{1,2,1},{1,1,2},{2,1,1},
{3,1,1},{1,3,1},{1,1,3},
{4,1,1},{1,4,1},{1,1,4},
};
vector> data2 = {
{5,4},{9,6},{4,7},{8,1},{3,4},{4,5},{5,6}
};
KDTree();
~KDTree();
Node* buildTree(vector> *data,Node *T);
void choiceSplit(vector> *data, int &split, vector &splitChoice);
};
#include "pch.h"
#include "KDTree.h"
int split_index = 0;
KDTree::KDTree()
{
}
KDTree::~KDTree()
{
}
bool equal(vector item1, vector item2) {
for (int i = 0; i < item1.size(); i++) {
if (item1.at(i) != item2.at(i)) {
return false;
}
}
return true;
}
string strMulInt(string str,int num) {
/*根据权重维度判别样本的大小*/
bool splitBigger(vector item1, vector item2) {
return item1.at(split_index) < item2.at(split_index);
}
/*
构建KD树
*/
Node* KDTree::buildTree(vector>* data, Node *t)
{
if (data->size() <= 0) {
return NULL;
}else{
/// 计算权重维度和中间值
int split;
vector splitChoice;
choiceSplit(data, split, splitChoice);
/// 申明左右子样本空间
vector> *left_data = new vector>, *right_data = new vector>;
/// 根据中间值将当前样本段分割成左样本空间和右样本空间
for (vector item : *data) {
/// 相同的元素不重复存入
/// 如果在权重维度上小于中间值则放入左样本空间,否则放入右样本空间
if (!equal(item, splitChoice)&&splitBigger(item,splitChoice)) {
left_data->push_back(item);
}
else if (!equal(item, splitChoice) && !splitBigger(item, splitChoice)) {
right_data->push_back(item);
}
}
/// 初始化根,并递归左右子空间
t =new Node(NULL);
t->data = new vector;
for (double v : splitChoice) {
t->data->push_back(v);
}
t->split = split;
t->left = buildTree(left_data, t->left);
t->right = buildTree(right_data, t->right);
for (double xi : *t->data) {
cout << xi << ' ';
}
cout << endl;
return t;
}
}
/*
选择该段样本空间的判别维度
*/
void KDTree::choiceSplit(vector>* data, int & split, vector &splitChoice)
{
vector weights;
/// 遍历样本空间的每一个维度,计算各个维度的权重(方差)
for (int j = 0; j < data->at(0).size(); j++) {
double temp1=0, temp2=0;
for (int i = 0; i < data->size(); i++) {
temp1 += 1.0 / (double)data->size()*data->at(i).at(j)*data->at(i).at(j);
temp2 += 1.0 / (double)data->size()*data->at(i).at(j);
}
temp2 *= temp2;
weights.push_back(temp1 - temp2);
}
/// 取最大者的维度为该段样本空间的判别维度
split = max_element(weights.begin(), weights.end()) - weights.begin();
split_index = split;
cout << "split:" << split << endl;
sort(data->begin(), data->end(), splitBigger);
splitChoice = data->at(data->size() / 2);
return;
}