通信信号与系统分析(二)
本篇主要介绍一下离散时间信号的基本运算。包括五部分,翻转运算,尺度变换,周期延拓,循环移位,卷积。
(一)翻转运算
设有序列x(n),它的翻转序列如下:
y(n)=x(-n)
注意:在翻转过程中,序列样值向量翻转的同时,位置向量翻转并取反。
在matlab中,翻转运算用fliplr函数实现,实现语句:
y=fliplr(x);
ny=-fliplr(nx);
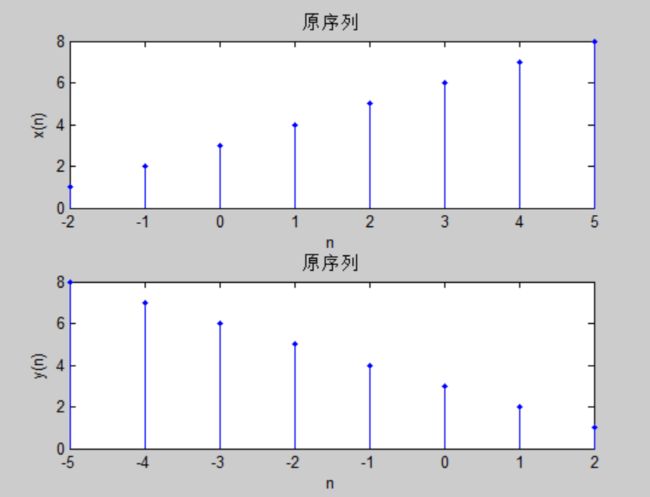
例题:用MATLAB实现序列x(n)={1,2,3,4,5,6,7,8},[-2,5]的翻转。clear all;
nx=-2:5;
x=1:8;
ny=-fliplr(nx);
y=fliplr(x);
subplot(2,1,1);
stem(nx,x,'.');
xlabel('n');ylabel('x(n)');title('原序列');
subplot(2,1,2);
stem(ny,y,'.');
xlabel('n');ylabel('y(n)');title('原序列');(二)尺度变换
序列x(n)的尺度变换序列如下:y(n)=x(mn),其中,m>1时代表序列的抽取,没隔m点取一点,0抽取,实现代码:
k=length(nx);
ny1=zeros(1,k);
y1=zeros(1,k);
for i=1:k
if(mod(nx(i),m)==0)
ny1(i)=nx(i)/m;
y1(i)=x(i);
end
end
插值实现代码:
设ny2=m*min(nx):m*max(nx),k1=length(ny2),y2=zeros(1,k1);
c=1;
for i=1:k
if(mod(ny2,m)==0)
y2(i)=x(c); 插值为0,因此判断条件改变
c=c+1;
end
end
因此我们可以编写一个函数实现抽样和插值:
function [ny1,y1,ny2,y2]=SeqCDBH(nx,x,m)
k=length(nx);
ny1=zeros(1,k);
y1=ny1;
ny2=m*min(nx):m*max(nx);
k1=length(ny2);
y2=zeros(1,k1);
for i=1:k%抽样
if(mod(nx,m)==0)
ny1=nx/m;
y1(i)=x(i);
end
end
c=1;
for i=1:k1;
if(mod(ny2,m)==0)
y2(i)=x(c);
c=c+1;
end
end
end(三)周期延拓
直接给出例子,读者慢慢领会:
function [ny,y]=SeqZQYT(nx,x,l,k)
%将序列x(n)以L为周期延拓,自x(n)的起点给出k个周期
N=length(nx);
ny=min(nx):k*l+min(nx)-1;
y=zeros(1,k*l);
for i=0:k*l-1
if L==N
y(i+1)=x(mod(i,L)+1);
end
if L>N %补零
x1=[x zeros(1,L-N)];
y(i+1)=x1(mod(i,L)+1);
end
if(LN/2)
x2=[x(1:N-L)+X(1+L:N) x(N-L+1:L)];
y(i+1)=x2(mod(i,L)+1);
end
if(L<=N/2)
if(mod(N,2)==1)
xb=[x,zeros(1,fix(N/2)-1)];
else
xb=[x,zeros(1,N/2)];
end
x3=xb(1:L);
if mod(N,L)==-1
for t=1:N/L-3
x3=x3+xb(1+t*L:(t+1)*L);
end
else
for i=1:fix(N/L)
x3=x3+xb(1+t*L:(t+1)*L);
end
end
y(i+1)=x3(mod(i,L)+1);
end
end
稍微解释一下代码:当L=N时候,将原序列左右平移即可,L>N,原序列需要补零。N/2(四)循环移位
实现过程:N点序列x(n)以N1为周期进行周期延拓,然后进行线性移位。
function [nxc,xc]=SeqCshift(nx,x,N,n0)
[nx1,x1]=SeqZQYT(nx,x,N,2);%N点序列
if n0>N
n0=mod(n0,N);
end
if n0<-N
n0=n0+N;
end
nxc=min(nx):min(nx)+N-1;
if n0>0
xc=x1(N-n0+1:2*N-n0);
else
xc=x1(abs(n0)+1:abs(n0)+N);
end