Leetcode学习之栈、队列、堆（1）

开宗明义：本系列基于小象学院林沐老师课程《面试算法 LeetCode 刷题班》，刷题小白，旨在理解和交流，重在记录，望各位大牛指点！

---

Leetcode学习之栈、队列、堆（1）

---

---

1、STL stack（栈、先进后出线性表）

堆栈是一个线性表，插入和删除只在表的一端进行。这一端称为栈顶($StackTop$)，另一端则为栈底($StackBottom$)。堆栈的元素插入称为入栈，元素的删除称为出栈。由于元素的入栈和出栈总在栈顶进行，因此，堆栈是一个后进先出(Last In First Out)表，即 $LIFO$ 表。$stack$堆栈容器的$C++$标准头文件为 $stack$ ，必须用宏语句 "#include " 包含进来，才可对 $stack$ 堆栈的程序进行编译。

测试代码：

#include 
#include 

using namespace std;
int main() {
	stack<int> s;
	if (s.empty())
		printf("s is empty\n");
	s.push(5);
	s.push(6);
	s.push(10);
	printf("s.top=%d\n", s.top());
	s.pop();
	s.pop();
	printf("s.top=%d\n", s.top());
	printf("s.size=%d\n", s.size());
	system("pause");
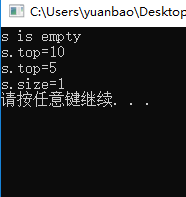
	return 0;
}

效果图：

stack用法总结：

empty() 堆栈为空则返回真
pop() 移除栈顶元素
push() 在栈顶增加元素
size() 返回栈中元素数目
top() 返回栈顶元素

---

2、STL queue（队列、先进先出线性表）

队列，先进先出的线性表。

测试代码：

#include 
#include 
using namespace std;

int main() {
	queue<int> Q;
	if (Q.empty()) {
		printf("Q is empty!\n");
	}
	Q.push(5);
	Q.push(6);
	Q.push(10);
	printf("Q.front = %d\n", Q.front());
	Q.pop();
	Q.pop();
	printf("Q.front = %d\n", Q.front());
	Q.push(1);
	printf("Q.back = %d\n", Q.back());
	printf("Q.size = %d\n", Q.size());
	system("pause");
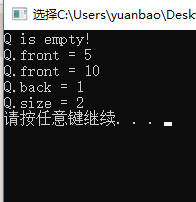
	return 0;
}

效果图：

queue用法总结：

push(x) 将x压入队列的末端
pop() 弹出队列的第一个元素(队顶元素)，注意此函数并不返回任何值
front() 返回第一个元素(队顶元素)
back() 返回最后被压入的元素(队尾元素)
empty() 当队列为空时，返回true
size() 返回队列的长度

---

3、使用队列实现栈（队列–>栈） Leetcode 225.

题目来源：$Leetcode225.ImplementStackUsingQueues$
题目描述：设计一个栈，支持如下操作 $push(x)、pop(x)、top()、empty()$，这些操作算法复杂度需是常数级，$O(1)$，需要实现的栈内部存储数据的结构为队列。
要求描述：
思路：临时队列

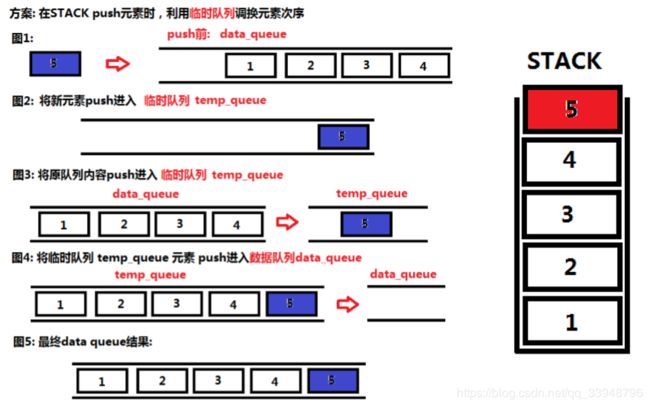
测试代码：

#include 
#include 

class Mystack {
public:
	Mystack(){}//构造函数

	void push(int x) {
		std::queue<int> temp_queue;
		temp_queue.push(x);//先将新元素push进入temp_queue
		while (!_data.empty())
		{
			temp_queue.push(_data.front());//将数据队列元素导入临时队列
			_data.pop();//消除
		}
		while (!temp_queue.empty())
		{
			_data.push(temp_queue.front());
			temp_queue.pop();
		}
	}

	int pop() {
		int x = _data.front();
		_data.pop();
		return x;
	}

	int top() {
		return _data.front();
	}

	bool empty() {
		return _data.empty();
	}

private:
	std::queue<int> _data; //数据是个队列
};

int main() {
	Mystack s;
	s.push(1);
	s.push(2);
	s.push(3);
	s.push(4);
	s.push(5);
	s.push(6);
	printf("%d\n",s.top());
	s.pop();
	printf("%d\n", s.top());
	s.pop();
	printf("%d\n", s.top());
	s.pop();
	system("pause");
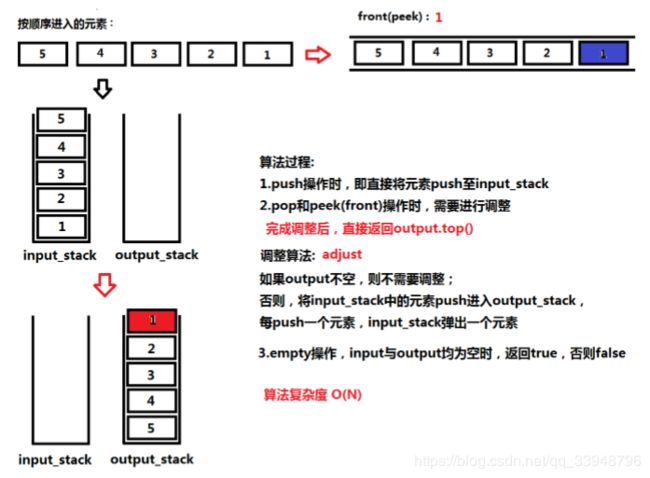
	return 0;
}

效果图：

---

4、使用栈实现队列（栈–>队列） Leetcode 232.

题目来源：$Leetcode232.ImplementQueueUsingStacks$
题目描述：设计一个队列，队列支持如下操作，这些操作的算法复杂度为常数级，$O(1)$，需要实现的队列内部存储数据的结构为栈，栈的方法只包括 $push、top、pop、size、empty$等标准的栈方法。
要求描述：

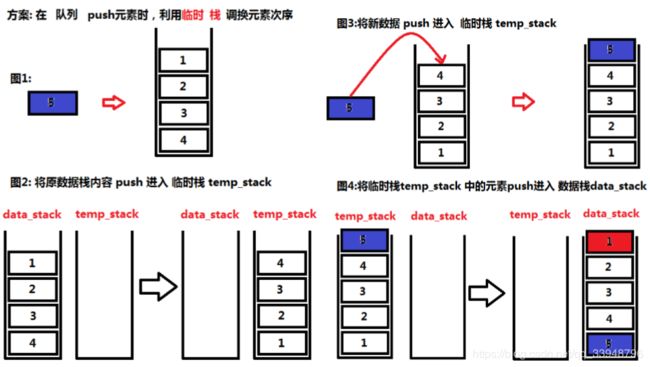
4.1 思路① 临时栈

测试代码：

#include 
#include 

using namespace std;

class MyQueue {
public:
	MyQueue(){}
	void push(int x) {
		stack<int> temp_stack;//临时栈
		while (!_data.empty())
		{
			temp_stack.push(_data.top()); //将stack的data的最后面top一下
			_data.pop();
		}
		temp_stack.push(x);//将新元素push到临时栈
		while (!temp_stack.empty())//将临时栈里面的元素push到数据栈中
		{
			_data.push(temp_stack.top());
			temp_stack.pop();
		}
	}
	int pop() {
		int x = _data.top();
		_data.pop();
		return x;
	}
	int top() {
		return _data.top();
	}
	bool empty() {
		return _data.empty();
	}

private:
	std::stack<int> _data;
};

4.2 思路② 双栈法 O(N)

测试代码：

#include 

class MyQueue {
public:
	MyQueue(){}
	void push(int x) {
		_input.push(x);//直接将 x push进入input
	}
	int pop() {
		adjust();//调整再进行pop()
		int x = _output.top();
		_output.pop();
		return x;
	}
	int peek() {
		adjust();//调整，并返回output_stack.top()
		return _output.top();
	}
	bool empty() {//当input_stak与output_stack同时为空，才返回true
		return _output.empty()&&_input.empty();
	}
private:
	void adjust() {
		if (!_output.empty()) {
			return;
		}
		while (!_input.empty()) {
			_output.push(_input.top());//将input_stack中每个元素input进去output_stack，每push一个就pop一个
			_input.pop();
		}
	}
	std::stack<int> _input;
	std::stack<int> _output;

};