基于用户预算的层次泊松矩阵分解推荐系统——论文学习第二篇
今天看了一篇论文:
Understanding users’ budgets for recommendation with hierarchical Poisson factorization
原文链接https://dl.acm.org/citation.cfm?id=3172135
但是对于很多概念都不理解,导致看得很艰难,在此对文中的一些概念进行总结,方便以后查阅。
- Gamma分布
- 泊松分布
- 平均场(mean-field)
- Kullback–Leibler divergence(相对熵,KL距离,KL散度)
- 共轭分布
- 变分推断(variational inference)
伽马(Gamma)分布
首先,Gamma function的表达式为
所以,有
而,Gamma分布即为
泊松(Poisson )分布
这篇博客讲解得很清晰易懂,泊松分布的前提是事件是独立的,且事件有固定的发生频率,如一家医院平均每小时有3个婴儿出生,而泊松分布就是预测某段时间内事件发生的概率,如接下来一小时一个婴儿也不出生的概率为
即,泊松分布的概率公式为
其中,N(t)为时间t的事件函数,n为事件发生的次数, λ λ 为泊松分布的参数,也就是事件发生的固定频率。
平均场(mean-field)
平均场是物理上的概念,这里简单用我自己的理解描述一下。平均场理论主要用于将复杂高维的问题简单化,如一个联合概率求解问题,参数之间互相影响,这样不利于概率的计算,于是将其他所有参数对某参数的影响之和反应到一个值上面,这样将联合概率分布转化为独立概率分布的乘积,在知乎上看到一个很易懂的例子,可以参考一下。
Kullback–Leibler divergence(相对熵,KL距离,KL散度)
KL距离是用来 衡量两个概率分布的差异,参考博客,衡量利用概率分布Q 拟合概率分布P 时的能量损耗,也就是说拟合以后丢失了多少的信息。
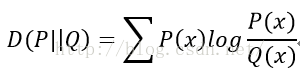
KL散度的值始终大于0,且Q和P的分布越相似则KL散度越小,并且当且仅当两分布相同时,KL散度等于0。
注意:KL散度是不对称的,即P对Q的散度与Q对P的散度不相等,且不满足三角不等式。
共轭(conjugate)分布
参考知乎的一个总结,共轭(conjugate)是贝叶斯方法中很常见的一个词,结合贝叶斯定理,我们可以将“共轭”理解为后验和先验是同一种分布。假设一组观测样本独立同分布于参数为 λ λ 的泊松分布,则伽马分布是参数 λ λ 的共轭先验(conjugate prior).即 xi∼Poisson(λ) x i ∼ Poisson ( λ ) , p(xi|λ)=e−λλxixi! p ( x i | λ ) = e − λ λ x i x i ! ,且 λ∼Gamma(α,β) λ ∼ Gamma ( α , β ) , p(λ|α,β)=βαΓ(α)e−βλλα−1 p ( λ | α , β ) = β α Γ ( α ) e − β λ λ α − 1 ,则有后验概率
变分推断(variational inference)
变分推断的目标是求出分布p,往往是后验概率P(z|x),很难求,于是改求一个分布q(z,v),用q去拟合p,当q和p非常接近时,输出q作为p的近似概率分布。在这个过程中,我们的关键点转变了,从“求分布”的推断问题,变成了“缩小距离”的优化问题。