python实现 最短路径算法
一、Floyd-Warshall算法
1.算法简介
Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。通常可以在任何图中使用,包括有向图、带负权边的图。
存储方式采用邻接矩阵
2.示例
| 0 | 1 | 2 | 6 | 3 |
| 1 | 0 | 3 | 5 | 2 |
| 2 | 3 | 0 | 8 | 5 |
| 6 | 5 | 8 | 0 | 3 |
| 3 | 2 | 5 | 3 | 0 |
3.代码实现
import math
nodes = ('A', 'B', 'C', 'D', 'E')
# dis矩阵为方阵
dis = [[0,1,2,math.inf,4],
[1,0,math.inf,8,2],
[2,math.inf,0,math.inf,6],
[math.inf,8,math.inf,0,3],
[4,2,6,3,0]]
def shortDistance(dis):
node_num = len(dis)
for i in range(node_num): # 十字交叉法的位置位置,先列后行
for j in range(node_num): # 列 表示dis[j][i]的值,即j->i
for k in range(j+1, node_num): # 行 表示dis[i][k]的值,即i->k,i只是一个桥梁而已
# 先列后行,形成一个传递关系,若比原来距离小,则更新
if dis[j][k] > dis[j][i] + dis[i][k]:
dis[j][k] = dis[j][i] + dis[i][k]
dis[k][j] = dis[j][i] + dis[i][k]二、分支界限算法
1.定义(解决单源最短路径问题)
与贪婪算法一样,这种方法也是用来为组合优化问题设计求解算法的,所不同的是它在问题的整个可能解空间搜索,所设计出来的算法虽其时间复杂度比贪婪算法高,但它的优点是与穷举法类似,都能保证求出问题的最佳解,而且这种方法不是盲目的穷举搜索,而是在搜索过程中通过限界,可以中途停止对某些不可能得到最优解的子空间进一步搜索(类似于人工智能中的剪枝),故它比穷举法效率更高。
2.优点
(1)边权可负(但是负权环路会造成死循环),而Dijkstra不行;
(2)保证最优解。
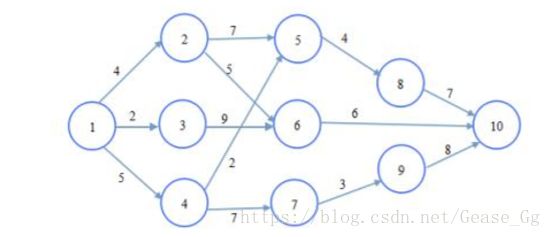
3.示例
分支界限解决策略
# 分支界限计算最短路径和最短路径长度
import math
from copy import deepcopy
# 初始化图参数 用字典初始初始化这个图
graph = {1: { 2: 4, 3: 2,4:5},
2: {5: 7, 6: 5},
3: {6: 9},
4: {5: 2, 7: 7},
5: {8: 4},
6: {10:6},
7: {9: 3},
8: {10:7},
9: {10:8},
10:{}
}
# 分支界限:计算起始节点到其他所有节点的最短距离
"""
1.将起始节点入队,并且初始化起始节点到其他所有节点距离为inf,用costs
2.检测起始节点的到子节点的距离是否变短,若是,则将其子节点入队
3.子节点全部检测完,则将起始节点出队,
4.让队列中的第一个元素作为新的起始节点,重复1,2,3,4
5.对队列为空,则退出循环
"""
# 数据结构:队列,树
def banch(graph, start):
costs = {} # 记录start到其他所有点的距离
trace = {start:[start]} # 记录start到其他所有点的路径
# 初始化costs
for key in graph.keys():
costs[key] = math.inf
costs[start] = 0
queue = [start] # 初始化queue
while len(queue) != 0:
head = queue[0] # 起始节点
for key in graph[head].keys(): # 遍历起始节点的子节点
dis = graph[head][key] + costs[head]
if costs[key] > dis:
costs[key] = dis
temp = deepcopy(trace[head]) # 深拷贝
temp.append(key)
trace[key] = temp# key节点的最优路径为起始节点最优路径+key
queue.append(key)
queue.pop(0) # 删除原来的起始节点
print(costs)
print(trace)
banch(graph, 1)