算法——最优解之动态规划

相应的练习代码：https://github.com/liuxuan320/Algorithm_Exercises

---

1. 动态规划的定义

动态规划作为一个非常优秀的算法被很多应用称为Optimal Algorithm
，也就是所谓的最优算法。它是一个总能找到最优解的算法，而它主要应用于多阶段决策的问题。但是，它也存在着一定的弊端，也就是准确度和效率不能并存，它一定能找到最优解，但是其时间复杂度通常都是幂指数，有很多应用只能在中小规模中实现，但这丝毫不影响动态规划的名声。下面我们给出动态规划的描述性语言：

无论过程的初始状态和初始决策是什么，其余的决策都必须相对于初始决策所产生的状态构成一个最有序列。

动态规划的核心主要是：状态转移。这个说法可能比较抽象，我们会在接下来的一个一个例子中，找到答案。

2. 多段图问题

1. 问题描述

多段图问题作为动态规划的入门问题，相对来讲是比较好理解的，其问题描述如下：

有一点S要到终点T，中间要经过若干段，每一段都有若各种走法，求出花费最少的路径。

这样的描述可能太过抽象，我们可以看下图

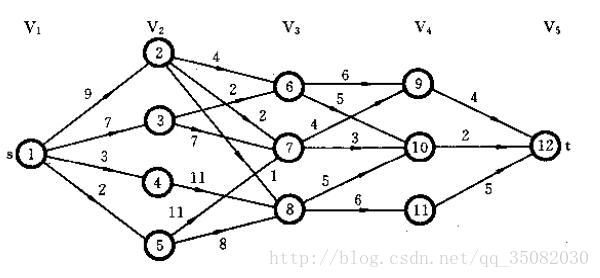
我们要从出发点1走到目标点12，中间需要走的段数有3段，分别有4个结点、3个结点、3个结点，那么我们怎么才能从这10个节点中，每个段中选择一个，最后拼出来最短路径呢？

2. 算法详解

这有点让我们想到了一个经典的问题，就是坐火车问题。我们这里使用向前处理法。也就是从12往前推，一段一段的靠到起点上。思路如下：
9，10，11这3个结点没有说的，只有一条路可以到达12，所以不用动。再往前看1段，在6,7,8这一段中，有3个结点，那么这三个结点怎么选择9,10,11节点后到达12结点最近呢，只需要通过计算后，就能知道每个结点的最短路径了，然后依次类推，直到到达出发路径。
思想就是这样，那么其核心公式就是
% COST(i,j)=minc(j,l)+COST(i+1,l) $

具体代码在Github上展示，这里我们只写出算法:

procedure FGRAPH(E,k，n,p)
//输入的按段的顺序给结点编号的，有n个结点的k段图。E是边集,c（i,j）是边<i,j>的成本。P（1：k）是最小成本路径。
    real COST(n)，integer D(n-1),P(k)，r,j,k,n
    COST(n)←0
    for j←n-1 to 1 by -1 do 
        设r 是一个这样的结点,(j,r)∈E且使c(j,r)+COST（r）取最小值
        COST（j）←c(j,r)+COST(r)
        D（j）←r
    repeat
    P(1)←1;P(k)←n
    for j←2 to k-1 do
        P(j)←D（P（j-1））
    repeat
end FGRAPH

这就是多段图的向前处理法。

3.最优二分检索

1.问题描述

我们之前讲过二分检索时，说二分检索已经是基于比较检索的时间下限了，那么最优二分检索是什么东西呢，我们之前讲二分检索时，每一个部分都是具有相同的先验概率的，但是如果我们的先验概率如果不一致时，如何进行检索呢，比如，我们常见到的猜物品价格的游戏，事实上，它的价格分布并不是均匀的，一个微波炉，显然大于1000的可能性比较小，因此正常的二分检做并不能达到最优， 这时候就需要最优二分检索树来帮忙了。
我们最优二分检索树的目标是：要使得检索的成本尽可能的小，无论查找到了还是没找到。

2. 算法详解

我们这里给出核心思想：
已知a(1:n),P(1:n),Q(0:n)
初始条件：w(i,i)=Q(i),C(i,i)=0,R(i,i)=0
公式：
C（i，j）=min{C(i,k-1)+C(k,j)}+W(i,j) (i

4. 0/1背包问题

1.问题描述

这里我们加了一个限制条件叫做0/1背包问题，和之前的背包问题不同的是，这个背包问题只能要么全部装进去，要么都不装进去，这样子，我们用之前的贪心算法并不能解决了，这时候，就要使用我们的动态规划的思想了，我们这里就介绍这个算法，它和我们前面两个问题不同，它采用的是状态转移的思想来解决。

2.算法详解

如果我们设 fj(x)是KNAP（i,j,x） 最优解的值
则 fn(m)=Max(fn−1(M),fn−1(M−Wn)+Pn)
这样，由递推关系就找到了，但是我们不用这方法，我们使用一种状态转移的方法。
由关系式可得 fi−1(M−Wi)+Pi是fi−1(X)向右平移Wi个单位向上平移Pi个单位叠加后取值较大的哪个，而那些转折点即为序偶
定义序偶为 (pi,wi),(p0,w0)=(0,0)
Si−1是fi−1的所有序偶集合，Si是fi−1(M−Wi)+Pi的所有序偶集合，把(wi,pi)加入到Si−1集合中，就得到了Si−11集合
但是这集合是有支配规则的：
1） wi≤wmax，即不能超过背包最大承重量
2） 对于wj≥wk，必须保证pj＞pk，否则要舍弃j>k
下面我们给出这个算法：
1. 首先 S0=(0,0)
2. 在 S0中每个元素都添加(p1,w1)形成s11，即(0+p1,0+w1)
3. 把S^0和S^1合并为S^1，即{(0,0),(p_1,w_1)}
4. 在S1中加入(p2,w2)形成S21，即(p2,w2),(p1+p2,w1+w2)
5. 合并S1和S21为S2，即(0,0),(p1,w1),(p2,w2),(p1+p2,w1+w2)
6. 依次加入2,3,4,5，..,n个物品直道全部添加完成。
不过要注意的是，合并时，要注意2个规则：
1. 最大W不能超过背包重量
2. 不能存在j,k使得 pj≤pk且wj>wk
以下是找到取放顺序：
1. 找到Sn中P最大且w≤wmax的，记为(ptemp,wtemp)
2. 若sn−1中不存在此(ptemp,wtemp)，则Xn置为1，(ptemp,wtemp)←(ptemp−pn,wtemp−wn),若sn−1中存在此(ptemp,wtemp),则Xn置为0
3. n←n-1,重复第二步骤，直道 X1 取完。
4. 输出X即为最终结果。

5. 可靠性设计

1.问题描述

可靠性设计的问题如下：
以串联方式联结n级设备，每级中以并联的方式连接多台设备，每台设备有不同的可靠性和成本，给定一定数量成本，求该系统的最大可靠性。

2.算法详解

同0/1背包问题一样，可靠性设计我们也使用状态转移序偶集来解决。但是与0/1背包问题不同的是：
1）每个 mi的取值不再只有0和1，而是有0，1，...,ui
2）每个结果不再是相加，而是相乘。
3）其支配规则除了原来两条外，其第二条不再是看成成本有无超过最大限制，而是看有无超过必要成本（每级一台）剩余后的成本。
我们很容易得到其递推关系：
fi(x)=maxΦi(mi)fi−1(x−cimi)
但是我们的做法是这样子的：
1. 算出到第i级最大可承受花费（约束规则1）
2. 算出每级最大可使用数(约束规则2)
3. 初始值为S^0={(1,0)}(因为相乘)
4. 计算每一级的可靠性 Pk=Pi∗(1−(1−Pj)n)，Pk是k级的可靠性，Pi是上一级的可靠性，Pj是当前级每一部件可靠性。
5. 回溯时，若Si中的解出现在si−1k中，则xi−1=k
至此，我们的可靠性设计算法就结束了，具体的代码可以到我的Github上访问。

6.流水线调度问题

1.问题描述

这个问题是一个经典问题，但是事实上，即使使用了动态规划，也没有办法解决这类问题，一般我们只能使用类似蚁群算法等一些智能算法来进行寻找最优近似解，从而不断的逼近最优解。
这里我们要讲的是一个非常简单的，只有2个流水线的的流水线调度问题。这里我们来描述这个问题：

假设在一条流水线上有n个作业，每个作业要求执行m个任务， T1i,T2i,..,Tmi，1≤i≤n，并且这个任务Tji只能在设备Pj上执行，1≤j≤m。并且对任一作业i，在任务Tj−1i没完成前，Tji不能执行，同一台设备在任何时刻不能同时处理一个以上的任务。

2. 算法详解

可以证明的是：在两台设备上处理的任务若不按作业的排列次序处理，则在调度完成时间上不比按次序处理弱。这里的证明我们不给出，其调度规则如下：
1. 把全部 ai和bi分类成非降序列
2. 按照这一分类次序考察此序列：
如果序列中下一个数是 aj 且作业j还没调度。
那么在还没使用的最左位置调度作业j
如果下个数是 bj 且作业j还没调度
那么在还没使用的最右位置调度作业j
如果已经调度了作业j，则转到下一个数。
这样就完成了流水线调度问题算法，下面我们举一个例子来说明这问题。
例：n=4,a=(3,4,8,10),b=(6,2,9,15)，求调度序列。
解：把a,b一起进行从小到大排列：
（2，3，4，6，8，9，10，15）
（ b2,a1,a2,b1,a3,b3,a4,b4 ）
最优序列为A1,A2,A3,A4，
1） b2 最小，A4=2
2） a1 最小，A1=1
3） a3 最小，A2=3
4） a4 最小，A3=4
总而言之，一句话：最小的 ai 放左边，最小的 bi 放右边。

7. 算法总结

这次我们讲解了算法中的动态规划的几个经典问题，包括两大类，一大类包括多段图和最优二分检索，另一大类包括0/1背包问题和货郎担问题的状态转移问题。动态规划这个算法十分有用，大家一定要好好体会。