NLP进阶之（一）Seq2Seq模型之Chatbot

1. 编码器—解码器（seq2seq）

NLP之前的章节中处理并分析了不定长的输入序列。但在很多应用中，输入和输出都可以是不定长序列。以机器翻译为例，输入可以是一段不定长的问题文本序列，输出可以是一段不定长的回答文本序列，例如

有 ， 现在 我 在 努力学习 英文 ， 我 想 成为 一名 翻译 。 嗯 ， 你 是 大有 前途 的 。 追逐 你 的 梦想 ， 永不 放弃 。

问题输入：“现在”、“我”、“在”、“努力学习”、“英文”、“，”、“我”、“想”、“成为”、“一名”、“翻译”、“。”

回输出：“嗯”、“，”、“你”、“是”、“大有”、“前途”、“的”、“。”、“追逐”、“你”、“的”、“梦想”、“，”、“永不”、“放弃”、“。”

解释

当输入输出都是不定长序列时，我们可以使用编码器—解码器（encoder-decoder）[1] 或者 seq2seq 模型 [2]。这两个模型本质上都用到了两个循环神经网络，分别叫做编码器和解码器。编码器用来分析输入序列，解码器用来生成输出序列。在训练数据集中，我们可以在每个句子后附上特殊符号“”（end of sequence）表示序列的终止。编码器每个时间步的输入依次为问题句子中的单词、标点和特殊符号“”。解码器在各个时间步中使用输入句子的编码信息和上个时间步的输出以及隐藏状态作为输入。
我们希望解码器在各个时间步能正确依次输出翻译后的问题单词、标点和特殊符号“”。
需要注意的是，解码器在最初时间步的输入用到了一个表示序列开始的特殊符号“”（beginning of sequence）。

接下来我们分别介绍编码器和解码器的定义。

1.1 编码器

编码器的作用是把一个不定长的输入序列变换成一个定长的背景变量 $\mathbf{c}$，并在该背景变量中编码输入序列信息。常用的编码器是循环神经网络。

让我们考虑批量大小为 1 的时序数据样本。假设输入序列是 $x_1,\dots ,x_T$，例如 $x_i$ 是输入句子中的第 $i$ 个词。在时间步 $t$，循环神经网络将输入 $x_t$ 的特征向量 ${\mathbf{x}}_t$ 和上个时间步的隐藏状态 ${\mathbf{h}}_{t-1}$ 变换为当前时间步的隐藏状态 ${\mathbf{h}}_t$。我们可以用函数 $f$ 表达循环神经网络隐藏层的变换：
$${\mathbf{h}}_t=f({\mathbf{x}}_t,{\mathbf{h}}_{t-1}).$$

接下来编码器通过自定义函数 $q$ 将各个时间步的隐藏状态变换为背景变量

$$\mathbf{c}=q({\mathbf{h}}_1,\dots ,{\mathbf{h}}_T).$$

例如，当选择 $q({\mathbf{h}}_1,\dots ,{\mathbf{h}}_T)={\mathbf{h}}_T$ 时，背景变量是输入序列最终时间步的隐藏状态 ${\mathbf{h}}_T$。以上描述的编码器是一个单向的循环神经网络，每个时间步的隐藏状态只取决于该时间步及之前的输入子序列。我们也可以使用双向循环神经网络构造编码器。这种情况下，编码器每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列（包括当前时间步的输入），并编码了整个序列的信息。

1.2 解码器

刚刚已经介绍，编码器输出的背景变量 $\mathbf{c}$ 编码了整个输入序列 $x_1,\dots ,x_T$ 的信息。给定训练样本中的输出序列 $y_1,y_2,\dots ,y_{T^{\prime }}$，对每个时间步 $t^{\prime }$（符号与输入序列或编码器的时间步 $t$ 有区别），解码器输出 $y_{t^{\prime }}$ 的条件概率将基于之前的输出序列 $y_1,\dots ,y_{t^{\prime }-1}$ 和背景变量 $\mathbf{c}$，即 $\mathbb{P}(y_{t^{\prime }}\mid y_1,\dots ,y_{t^{\prime }-1},\mathbf{c})$。

为此，我们可以使用另一个循环神经网络作为解码器。在输出序列的时间步 $t^{\prime }$，解码器将上一时间步的输出 $y_{t^{\prime }-1}$ 以及背景变量 $\mathbf{c}$ 作为输入，并将它们与上一时间步的隐藏状态 ${\mathbf{s}}_{t^{\prime }-1}$ 变换为当前时间步的隐藏状态 ${\mathbf{s}}_{t^{\prime }}$。因此，我们可以用函数 $g$ 表达解码器隐藏层的变换：

$${\mathbf{s}}_{t^{\prime }}=g(y_{t^{\prime }-1},\mathbf{c},{\mathbf{s}}_{t^{\prime }-1}).$$

有了解码器的隐藏状态后，我们可以使用自定义的输出层和softmax运算来计算 $\mathbb{P}(y_{t^{\prime }}\mid y_1,\dots ,y_{t^{\prime }-1},\mathbf{c})$，例如基于当前时间步的解码器隐藏状态 ${\mathbf{s}}_{t^{\prime }}$、上一时间步的输出 $y_{t^{\prime }-1}$ 以及背景变量 $\mathbf{c}$ 来计算当前时间步输出 $y_{t^{\prime }}$ 的概率分布。

1.3 模型训练

根据最大似然估计，我们可以最大化输出序列基于输入序列的条件概率

$$\begin{array}{rl}\mathbb{P}(y_1,\dots ,y_{T^{\prime }}\mid x_1,\dots ,x_T)& =\prod _{t^{\prime }=1}^{T^{\prime }}\mathbb{P}(y_{t^{\prime }}\mid y_1,\dots ,y_{t^{\prime }-1},x_1,\dots ,x_T)\\ & =\prod _{t^{\prime }=1}^{T^{\prime }}\mathbb{P}(y_{t^{\prime }}\mid y_1,\dots ,y_{t^{\prime }-1},\mathbf{c}),\end{array}$$
并得到该输出序列的损失

$$-\log \mathbb{P}(y_1,\dots ,y_{T^{\prime }}\mid x_1,\dots ,x_T)=-\sum _{t^{\prime }=1}^{T^{\prime }}\log \mathbb{P}(y_{t^{\prime }}\mid y_1,\dots ,y_{t^{\prime }-1},\mathbf{c}),$$

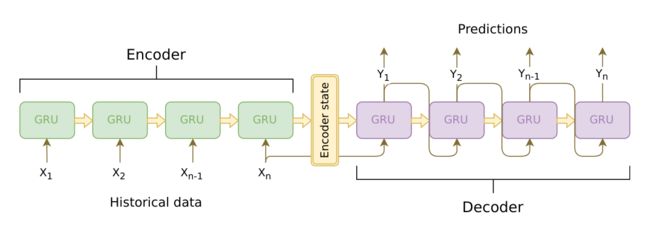
在模型训练中，所有输出序列损失的均值通常作为需要最小化的损失函数。入上图所描述的模型预测中，我们需要将解码器在上一个时间步的输出作为当前时间步的输入。与此不同，在训练中我们也可以将标签序列在上一个时间步的标签作为解码器在当前时间步的输入。这叫做强制教学（teacher forcing）。

1.4 参考文献

引用文本
[1] Cho, K., Van Merri ë nboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
[2] Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with neural networks. In Advances in neural information processing systems (pp. 3104-3112).

2. 注意力机制（Attention）

注意力机制如下图所示：

2.1 注意力机制背景

在编码器—解码器（seq2seq）的应用中，机器翻译是最广为人知的应用。解码器在各个时间步依赖相同的背景变量来获取输入序列信息。当编码器为循环神经网络时，背景变量来自它最终时间步的隐藏状态。

以机器翻译为具体例子：输入为英语序列“They”、“are”、“watching”、“.”，输出为法语序列“Ils”、“regardent”、“.”。不难想到，解码器在生成输出序列中的每一个词时可能只需利用输入序列某一部分的信息。例如，在输出序列的时间步 1，解码器可以主要依赖“They”、“are”的信息来生成“Ils”，在时间步 2 则主要使用来自“watching”的编码信息生成“regardent”，最后在时间步 3 则直接映射句号“.”。这看上去就像是在解码器的每一时间步对输入序列中不同时间步的编码信息分配不同的注意力一样。这也是注意力机制的由来 。

仍然以循环神经网络为例，注意力机制通过对编码器所有时间步的隐藏状态做加权平均来得到背景变量。解码器在每一时间步调整这些权重，即注意力权重，从而能够在不同时间步分别关注输入序列中的不同部分并编码进相应时间步的背景变量。本节我们将讨论注意力机制是怎么工作的。
在“编码器—解码器（seq2seq）”上面的说明里我们区分了输入序列或编码器的索引 $t$ 与输出序列或解码器的索引 $t^{\prime }$ 。该节中，解码器在时间步 $t^{\prime }$ 的隐藏状态 ${\mathbf{s}}_{t^{\prime }}=g({\mathbf{y}}_{t^{\prime }-1},\mathbf{c},{\mathbf{s}}_{t^{\prime }-1})$ ，其中 ${\mathbf{y}}_{t^{\prime }-1}$ 是上一时间步 $t^{\prime }-1$ 的输出 $y_{t^{\prime }-1}$ 的特征表示，且任一时间步 $t^{\prime }$ 使用相同的背景变量 $\mathbf{c}$ 。但在注意力机制中，解码器的每一时间步将使用可变的背景变量。记 ${\mathbf{c}}_{t^{\prime }}$ 是解码器在时间步 $t^{\prime }$ 的背景变量，那么解码器在该时间步的隐藏状态可以改写为

$${\mathbf{s}}_{t^{\prime }}=g({\mathbf{y}}_{t^{\prime }-1},{\mathbf{c}}_{t^{\prime }},{\mathbf{s}}_{t^{\prime }-1}).$$

这里的关键是如何计算背景变量 ${\mathbf{c}}_{t^{\prime }}$ 和如何利用它来更新隐藏状态 ${\mathbf{s}}_{t^{\prime }}$ 。以下将分别描述这两个关键点。

2.2 计算背景变量

图2描绘了注意力机制如何为解码器在时间步 2 计算背景变量。首先，函数 $a$ 根据解码器在时间步 1 的隐藏状态和编码器在各个时间步的隐藏状态计算softmax运算的输入。Softmax 运算输出概率分布并对编码器各个时间步的隐藏状态做加权平均，从而得到背景变量。

具体来说，令编码器在时间步 $t$ 的隐藏状态为 ${\mathbf{h}}_t$ ，且总时间步数为 $T$。那么解码器在时间步 $t^{\prime }$ 的背景变量为所有编码器隐藏状态的加权平均：

$${\mathbf{c}}_{t^{\prime }}=\sum _{t=1}^T{\alpha }_{t^{\prime }t}{\mathbf{h}}_t,$$

其中给定 $t^{\prime }$ 时，权重 ${\alpha }_{t^{\prime }t}$ 在 $t=1,\dots ,T$ 的值是一个概率分布。为了得到概率分布，我们可以使用softmax运算:

$${\alpha }_{t^{\prime }t}=\frac{\exp (e_{t^{\prime }t})}{{\sum }_{k=1}^T\exp (e_{t^{\prime }k})},t=1,\dots ,T.$$

现在，我们需要定义如何计算上式中softmax运算的输入 $e_{t^{\prime }t}$ 。由于 $e_{t^{\prime }t}$ 同时取决于解码器的时间步 $t^{\prime }$ 和编码器的时间步 $t$ ，我们不妨以解码器在时间步 $t^{\prime }-1$ 的隐藏状态 ${\mathbf{s}}_{t^{\prime }-1}$ 与编码器在时间步 $t$ 的隐藏状态 ${\mathbf{h}}_t$ 为输入，并通过函数 $a$ 计算 $e_{t^{\prime }t}$ ：

$$e_{t^{\prime }t}=a({\mathbf{s}}_{t^{\prime }-1},{\mathbf{h}}_t).$$

这里函数 $a$ 有多种选择，如果两个输入向量长度相同，一个简单的选择是计算它们的内积 $a(\mathbf{s},\mathbf{h})={\mathbf{s}}^{\top }\mathbf{h}$ 。而最早提出注意力机制的论文则将输入连结后通过含单隐藏层的多层感知机变换 ：

$$a(\mathbf{s},\mathbf{h})={\mathbf{v}}^{\top }\tanh ({\mathbf{W}}_s\mathbf{s}+{\mathbf{W}}_h\mathbf{h}),$$

其中 $\mathbf{v}$ 、 ${\mathbf{W}}_s$ 、 ${\mathbf{W}}_h$ 都是可以学习的模型参数。

// Attention Model
def attention_model(attention_size):
    model = nn.Sequential()
    model.add(nn.Dense(attention_size, activation='tanh', use_bias=False,
                       flatten=False),
              nn.Dense(1, use_bias=False, flatten=False))
    return model

def attention_forward(model, enc_states, dec_state):
    # 将解码器隐藏状态广播到跟编码器隐藏状态形状相同后进行连结。广播的目的是将所有的向量进行结合
    dec_states = nd.broadcast_axis(
        dec_state.expand_dims(0), axis=0, size=enc_states.shape[0])
    enc_and_dec_states = nd.concat(enc_states, dec_states, dim=2)
    e = model(enc_and_dec_states)  # 形状为（时间步数，批量大小，1）。
    alpha = nd.softmax(e, axis=0)  # 在时间步维度做 softmax 运算。
    return (alpha * enc_states).sum(axis=0)  # 返回背景变量。
    
seq_len, batch_size, num_hiddens = 10, 4, 8
model = attention_model(10)
model.initialize()
enc_states = nd.zeros((seq_len, batch_size, num_hiddens))
dec_state = nd.zeros((batch_size, num_hiddens))
attention_forward(model, enc_states, dec_state).shape

---

output:(4, 8)

2.3 矢量化计算

我们还可以对注意力机制采用更高效的矢量化计算。广义上，注意力机制模型的输入包括查询项以及一一对应的键项和值项。其中值项是需要加权平均的一组项。在加权平均中，值项的权重来自查询项以及与该值项对应的键项的计算。

在上面的例子中，查询项为解码器的隐藏状态，键项和值项均为编码器的隐藏状态。
让我们考虑一个常见的简单情形，即编码器和解码器的隐藏单元个数均为 $h$，且函数 $a(\mathbf{s},\mathbf{h})={\mathbf{s}}^{\top }\mathbf{h}$。假设我们希望根据解码器单个隐藏状态 ${\mathbf{s}}_{t^{\prime }-1}\in {\mathbb{R}}^h$ 和编码器所有隐藏状态 ${\mathbf{h}}_t\in {\mathbb{R}}^h,t=1,\dots ,T$ 计算背景向量 ${\mathbf{c}}_{t^{\prime }}\in {\mathbb{R}}^h$ 。
我们可以将查询项矩阵 $\mathbf{Q}\in {\mathbb{R}}^{1\times h}$ 设为 ${\mathbf{s}}_{t^{\prime }-1}^{\top }$ ，并令键项矩阵 $\mathbf{K}\in {\mathbb{R}}^{T\times h}$ 和值项矩阵 $\mathbf{V}\in {\mathbb{R}}^{T\times h}$ 相同且第 $t$ 行均为 ${\mathbf{h}}_t^{\top }$。此时，我们只需要通过矢量化计算

$$\text{softmax}(\mathbf{Q}{\mathbf{K}}^{\top })\mathbf{V}$$

即可算出转置后的背景向量 ${\mathbf{c}}_{t^{\prime }}^{\top }$。当查询项矩阵 $\mathbf{Q}$ 的行数为 $n$ 时，上式将得到 $n$ 行的输出矩阵。输出矩阵与查询项矩阵在相同行上一一对应。

2.4 更新隐藏状态

以门控循环单元为例，在解码器中我们可以对门控循环单元的设计稍作修改 [1]。解码器在时间步 $t^{\prime }$ 的隐藏状态为

$${\mathbf{s}}_{t^{\prime }}={\mathbf{z}}_{t^{\prime }}\odot {\mathbf{s}}_{t^{\prime }-1}+(1-{\mathbf{z}}_{t^{\prime }})\odot {\tilde{\mathbf{s}}}_{t^{\prime }},$$

其中的重置门、更新门和候选隐含状态分别为

$$\begin{array}{rl}{\mathbf{r}}_{t^{\prime }}& =\sigma ({\mathbf{W}}_{yr}{\mathbf{y}}_{t^{\prime }-1}+{\mathbf{W}}_{sr}{\mathbf{s}}_{t^{\prime }-1}+{\mathbf{W}}_{cr}{\mathbf{c}}_{t^{\prime }}+{\mathbf{b}}_r),\\ {\mathbf{z}}_{t^{\prime }}& =\sigma ({\mathbf{W}}_{yz}{\mathbf{y}}_{t^{\prime }-1}+{\mathbf{W}}_{sz}{\mathbf{s}}_{t^{\prime }-1}+{\mathbf{W}}_{cz}{\mathbf{c}}_{t^{\prime }}+{\mathbf{b}}_z),\\ {\tilde{\mathbf{s}}}_{t^{\prime }}& =\text{tanh}({\mathbf{W}}_{ys}{\mathbf{y}}_{t^{\prime }-1}+{\mathbf{W}}_{ss}({\mathbf{s}}_{t^{\prime }-1}\odot {\mathbf{r}}_{t^{\prime }})+{\mathbf{W}}_{cs}{\mathbf{c}}_{t^{\prime }}+{\mathbf{b}}_s),\end{array}$$

其中含下标的 $\mathbf{W}$ 和 $\mathbf{b}$ 分别为门控循环单元的权重参数和偏差参数。

3. 小结

• 我们可以在解码器的每个时间步使用不同的背景变量，并对输入序列中不同时间步编码的信息分配不同的注意力。
• 广义上，注意力机制模型的输入包括查询项以及一一对应的键项和值项。
• 注意力机制可以采用更为高效的矢量化计算。

3.1 参考链接

[1]: Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473.