数据结构---图的详细介绍
前言:
In order to change we must be sick and tired of being sick and tired.
Name:WIllam
Time:2017/2/25
1、名词解释:
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
图按照边的有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
图按照边或弧的多少分稀疏图和稠密图。如果图中的任意两个顶点之间都存在边叫做完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
图上的边或弧带有权则称为网。
图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复的叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称为强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称为强连通分量。
无向图中连通且n个顶点n-1条边称为生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
2、图的存储结构—-邻接矩阵
图的邻接矩阵的表示方式需要两个数组来表示图的信息,一个一维数组表示每个数据元素的信息,一个二维数组(邻接矩阵)表示图中的边或者弧的信息。
如果图有n个顶点,那么邻接矩阵就是一个n*n的方阵,方阵中每个元素的值的计算公式如下:

邻接矩阵表示图的具体示例如下图所示:
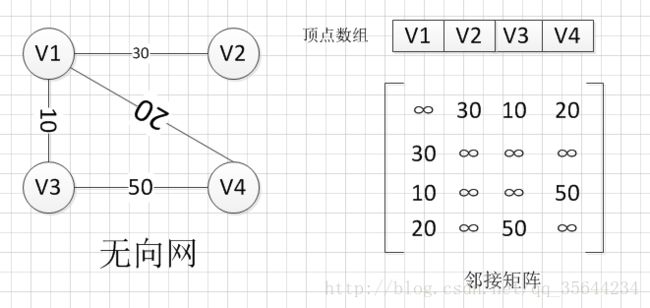
首先给个无向图的实例:
OK,到这里为止,我们给出一个无向图的邻接矩阵和一个有向图的邻接矩阵,我们可以从这两个邻接矩阵得出一些结论:
- 无向图的邻接矩阵都是沿对角线对称的
- 要知道无向图中某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
- 对于有向图,要知道某个顶点的出度,其实就是这个顶点vi在邻接矩阵中第i行的元素之和,如果要知道某个顶点的入度,那就是第i列的元素之和。
但是,如果我们需要表示的图是一个网的时候,例如假设有个图有n个顶点,同样该网的邻接矩阵也是一个n*n的方阵,只是方阵元素的值的计算方式不同,如下图所示:

这里的wij表示两个顶点vi和vj边上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值。下面是具体示例,表示的一个有向网的图和邻接矩阵:
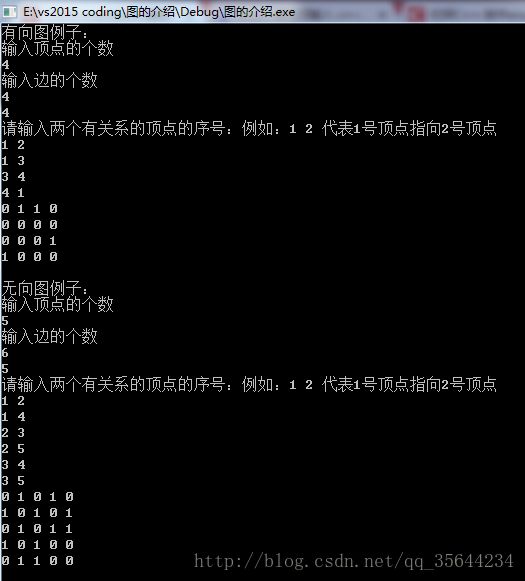
3、图的存储结构—-邻接矩阵的代码实现
#include4、图的存储结构—-邻接矩阵的优缺点
- 优点:
直观、容易理解,可以很容易的判断出任意两个顶点是否有边,最大的优点就是很容易计算出各个顶点的度。 - 缺点:
当我么表示完全图的时候,邻接矩阵是最好的表示方法,但是对于稀疏矩阵,由于它边少,但是顶点多,这样就会造成空间的浪费。
5、 图的存储结构—邻接表
邻接表是图的一种链式存储结构。主要是应对于邻接矩阵在顶点多边少的时候,浪费空间的问题。它的方法就是声明两个结构。如下图所示:
OK,我们虽然知道了邻接表是这两个结构来表示图的,那么它的怎么表示的了,不急,我们先把它转为c++代码先,然后,再给个示例,你就明白了。
typedef char Vertextype;
//表结点结构
struct ArcNode {
int adjvex; //某条边指向的那个顶点的位置(一般是数组的下标)。
ArcNode * nextarc; //指向下一个表结点
int weight; //这个只有网图才需要使用。普通的图可以直接忽略
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode * firstarc; //指向第一条依附在该顶点边的信息(表结点)
};无向图的示例:
从图中我们可以知道,顶点是通过一个头结点类型的一维数组来保存的,其中我们每个头结点的firstarc都是指向第一条依附在该顶点边的信息,表结点的adjvex表示的该边的另外一个顶点在顶点数组中的下标,weight域对于普通图是无意义的,可以忽略,nextarc指向的是下一条依附在该顶点的边的信息。
下面再给出一个有向图的例子:
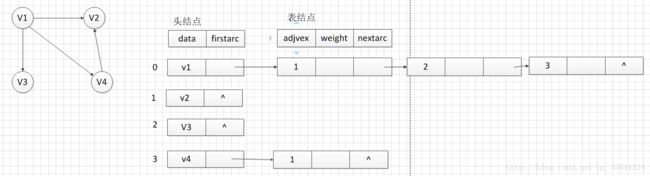
通过上述的两个例子,我们应该明白邻接表是如何进行表示图的信息的了。
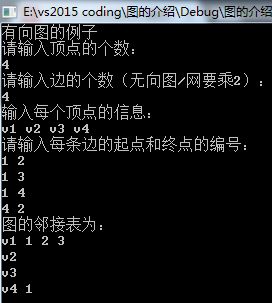
6、图的存储结构—-邻接表的代码实现
#include7、图的存储结构—-邻接表的优缺点
- 优点:
对于,稀疏图,邻接表比邻接矩阵更节约空间。 - 缺点:
不容易判断两个顶点是有关系(边),顶点的出度容易,但是求入度需要遍历整个邻接表。
8、有向图的存储结构—-十字链表
十字链表是有向图的一个专有的链表结构,我们之前也说了,邻接表对于我们计算顶点的入度是一个很麻烦的事情,而十字链表正好可以解决这个问题。十字链表和邻接表一样,他会有两个结构来表示图:其中一个结构用于保存顶点信息,另外一个结构是用于保存每条边的信息,如下图所示:

同样,我们知道头结点就是用于保存每个顶点信息的结构,其中data主要是保存顶点的信息(如顶点的名称),firstin是保存第一个入度的边的信息,firstout保存第一个出度的边的信息。其中,表结点就是记录每条边的信息,其中tailvex是记录这条边弧头的顶点的在顶点表中的下标(不是箭头那个),headvex则是记录弧尾对应的那个顶点在顶点表中的下标(箭头的那个),hlink是指向具有下一个具有相同的headvex的表结点,tlink指向具有相同的tailvex的表结点,weight是表示边的权重(网图才需要使用)。具体的代码表示如下:
typedef string Vertextype;
//表结点结构
struct ArcNode {
int tailvex; //弧尾的下标,一般都是和对应的头结点下标相同
int headvex; //弧头的下标
ArcNode * hlink; //指向下一个弧头同为headvex的表结点 ,边是箭头的那边
ArcNode * tlink; //指向下一个弧尾为tailvex的表结点,边不是箭头的那边
int weight; //只有网才会用这个变量
};
//头结点
struct Vnode
{
Vertextype data; //这个是记录每个顶点的信息(现在一般都不需要怎么使用)
ArcNode *firstin; //指向第一条(入度)在该顶点的表结点
ArcNode *firstout; //指向第一条(出度)在该顶点的表结点
};其实,这个自己也可以去尝试手画一个十字链表出来,其实都是很简单的
9、有向图的存储结构—-十字链表代码实现
#include10、无向图的存储结构—-邻接多重表
邻接多重表是无向图的另一种链式存储结构。我们之前也说了使用邻接矩阵来存储图比价浪费空间,但是如果我们使用邻接表来存储图时,对于无向图又有一些不便的地方,例如我们需要对一条已经访问过的边进行删除或者标记等操作时,我们除了需要找到表示同一条边的两个结点。这会给我们的程序执行效率大打折扣,所以这个时候,邻接多重表就派上用场啦。
首先,邻接多重表同样是对邻接表的一个改进得到来的结构,它同样需要一个头结点保存每个顶点的信息和一个表结点,保存每条边的信息,他们的结构如下:

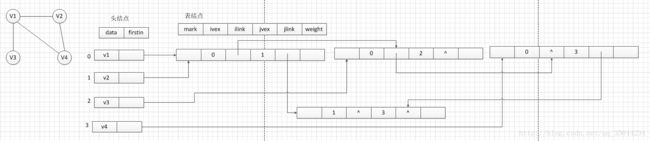
其中,头结点的结构和邻接表一样,而表结点中就改变比较大了,其中mark为标志域,例如标志是否已经访问过,ivex和jvex代表边的两个顶点在顶点表中的下标,ilink指向下一个依附在顶点ivex的边,jlink指向下一个依附在顶点jvex的边,weight在网图的时候使用,代表该边的权重。
下面是一个无向图的邻接多重表的实例(自己也可以尝试去画画,具体的原理都是很简单的):
11、无向图的存储结构—-邻接多重表代码实现
#include