pytorch学习笔记（二）

pytorch学习笔记（二）

1.前言

在之前我们已经粗略看了看autograd函数，现在我们要用到的torch.nn是基于autograd来定义和区分各种模型。

一个简单的典型神经网络训练过程通常包含以下过程：

• 定义一个有一些可学习参数的神经网络

• 循环训练数据集

• 处理网络中的输入

• 计算损失（输出与正确结果间的差别）

• 回传梯度给神经网络中的参数

• 更新网络的权重，典型的简单更新规则：
  

  weight=weight−learning.rate∗gradient w e i g h t = w e i g h t − l e a r n i n g . r a t e ∗ g r a d i e n t

2.定义一个简单的网络

先上代码

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        #1 input image channel,6 output channels,5x5 square convolution kernel
        self.conv1=nn.Conv2d(1,6,5)#生成一个1输入6输出的5x5的卷基层
        self.conv2=nn.Conv2d(6,16,5)#生成一个6输入16输出的5x5的卷基层
        #an affine operation:y=wx+b
        self.fc1=nn.Linear(16*5*5,120)#生成一个16*5*5输入120输出的线性变换层
        self.fc2=nn.Linear(120,84)#生成一个120输入84输出的线性变换层
        self.fc3=nn.Linear(84,10)#生成一个84输入10输出的线性变换层

    def forward(self,x):
        #Max pooling over a (2,2) window
        x = F.max_pool2d(F.relu(self.conv1(x)),(2,2))
        #If the sie is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)),2)
        x = x.view(-1,self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return  x

    def num_flat_features(self,x):
        size = x.size()[1:]
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

来一点点看这个代码

首先对于python类函数不太了解的建议去学习一下

super()函数是一个继承父类调用的一个函数，就是包含了父类函数的所有性质

nn.Conv2d和nn.Linear两个函数都有注释标明

下面看看forward函数里面一些东西

2.1 relu函数

relu函数是神经网络中的一种激活函数，激活函数是用来加入非线性因素的，提高神经网络对模型的表达能力，解决线性模型所不能解决的问题。

relu(x)=max(0,x) r e l u ( x ) = m a x ( 0 , x )

2.2 max_pool2d

max_pool2d是一类池化函数，池化函数的结果是使得特征减少，参数减少，但池化的目的并不仅在于此，池化目的是为了保持某种不变性（旋转、平移、伸缩等），常用的有mean-pooling，max-pooling和Stochastic-pooling三种。这里用到的就是最大池化函数，能更多地保留纹理信息。

这里用到的是一个2*2的最大池化函数，如图所示，得到的是每个池化区域的最大的值，并且池化模块扫过每个区域不会有重叠部分，这样能更好的提取整个图片的纹理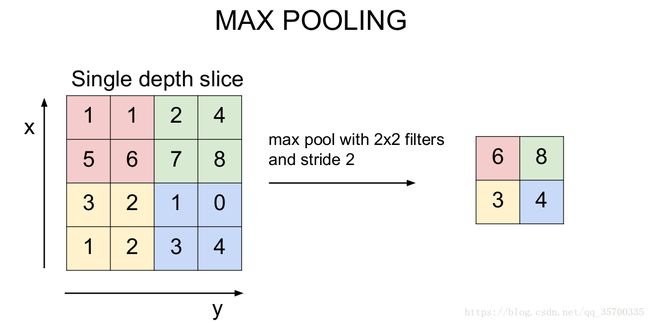

2.3 view函数

这个是把一个矩阵重新排列成不同维度但不改变元素的函数，如代码中x.view(-1,self.num_flat_features(x))，这里-1就是把后面的矩阵展成一维数组，以便后面线性变换层操作

2.4 num_flat_features

num_flat_features函数是把经过两次池化后的16x5x5的矩阵组降维成二维，便于view函数处理，而其中用乘法也是为了不丢失每一层相关的特性

后面的就比较直观了，所以这个神经网络整个的过程如下：

input−>conv2d−>relu−>maxpool2d−>conv2d−>relu−>maxpool2d−>flat−>view−>linear−>relu−>linear−>relu−>linear i n p u t − > c o n v 2 d − > r e l u − > m a x p o o l 2 d − > c o n v 2 d − > r e l u − > m a x p o o l 2 d − > f l a t − > v i e w − > l i n e a r − > r e l u − > l i n e a r − > r e l u − > l i n e a r

先看看这一层的输出：

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

即表明了每个函数的内部参数的规格

接下来试试这个网络吧，我们随机定义一个32x32的输入

input = torch.randn(1,1,32,32)#一个32x32的矩阵
out = net(input)
print(out)

输出：

tensor([[ 0.1135, -0.1450,  0.0856,  0.0570,  0.0407,  0.0201,  0.0003, -0.0370,
          0.1637, -0.0669]], grad_fn=)

这时候我们并不能看出来有这有什么意义，继续往下走

3.损失函数

损失函数就是估计我们得到的输出和目标的偏差，当然，越小越好啦，损失函数有很多，这就不一一赘述，这里我们用一个简单计算输出与目标平方均值误差nn.MSELoss

ℓ(x,y)=L={l1,…,lN}⊤,ln=(xn−yn)2, ℓ ( x , y ) = L = { l 1 , … , l N } ⊤ , l n = ( x n − y n ) 2 ,

ℓ(x,y)={mean(L),sum(L),ifsize_average=True,ifsize_average=False. ℓ ( x , y ) = { mean ⁡ ( L ) , if size_average = True , sum ⁡ ( L ) , if size_average = False .

这里我们用到的是mean(L)

output = net(input)
target = torch.randn(10)#a dummy target,for example
target = target.view(1,-1)#make it the sanme shape as output
criterion = nn.MSELoss()

loss = criterion(output,target)
print(loss)

这里的target使我们随便生成的一个数组作为示例

输出：

tensor(1.1111, grad_fn=)#随便输出就是单身的象征。。

4.Backprop

我们只需要一个loss.backward()函数就可以反向传播这个损失，但我们需要事先清除已经存在的梯度是指，不然梯度就会累加到现存的梯度上

net.zero_grad()#zeros the gradient buffers of all parameters

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

输出：

conv1.bias.grad before backward
None
conv1.bias.grad after backward
tensor([-0.0002,  0.0057,  0.0014, -0.0019,  0.0007,  0.0036])

这样我们就完成了计算loss以及把相应的参数回传

5.更新权重

实际中用的最简单的更新法则就是随机梯度下降（SGD）：

weight=weight−learning.rate∗gradient w e i g h t = w e i g h t − l e a r n i n g . r a t e ∗ g r a d i e n t

代码也比较简单：

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate )

但是我们不能总是像这样去定义权重更新规则，torch.optim里面提供了我们基本能用到的大部分的规则使用也非常简单

import torch.optim as optim
#create your optimizer
optimizer = optim.SGD(net.parameters(),lr=0.01)

#in your train loop:
optimizer.zero_grad()
output = net(input)
loss = criterion(output,target)
loss.backward()python
optimizer.step()#Does the update

6.小结

简单的完成了一个神经网络的架构，这也只是帮助理解，并不是说后面就能直接用这些解决问题了，还有很多是还没解决的，不过下次我们来试试简单训练一个分类器