卷积神经网络架构理解
神经网络基础
神经网络属于优化类的数学模型。每个神经元接收到输入后,经过一些计算操作后输出一个特定的数值。这个数值经过一个激活函数(非线性的),产生这个神经元的最后输出。有很多激活函数,且绝大数已经在Tensorflow中集成了,最流行的是 S i g m o i d Sigmoid Sigmoid函数:
y = 1 1 + e − z z = w T x + b y=\frac{1}{1+e^{-z}}\\ z=w^Tx+b y=1+e−z1z=wTx+b
z z z是线性计算结果, w w w是权重向量, x x x是输入向量, b b b是偏置项。公式中,不过是把图中的累加更改成了向量的内积形式,这在机器学习中很常见,向量化计算可以节约大量时间。
单个神经元模型:

整体全连接神经网络模型:
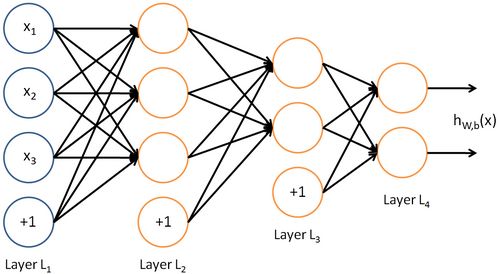
每一层添加一个偏置项。具体的数学推导,参见这篇博客
#卷积神经网络
##常用的操作与名词:
这一部分,总结了看论文或者有关博客时,遇到的专用名词:
Input/Output Volumes:
CNN把输入的图片视为矩阵,当然,这是在灰度图片的情况下的。加入我们有一张256色图片作为输入,那么图片的矩阵的每个像素点取值为[0,255]。然而,彩色的图片进行灰度处理会丢失很多信息,于是就多了一层输入。一般RGB三原色图像,可以分解成红、绿、蓝三个颜色层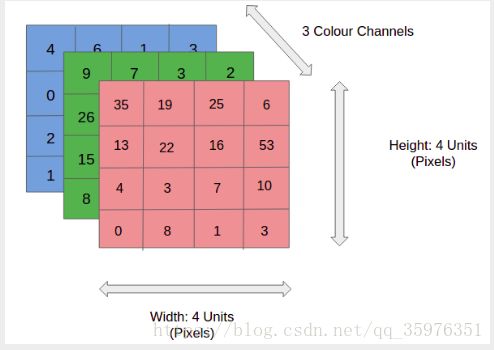
每一个颜色层相当于一个channel
###Filters:
过滤器。相当于一次信息过滤操作,也可以看成一次像素的编码操作的标准。一个过滤器的大小一般小于图片,之后对过过滤器范围内的像素进行一次内积,然后累加。比如参照Kernel Operations的图片,红色矩阵中的黑框就相当于一个过滤器。过滤器的作用可以看成一次局部感知,同时减少权重参数的数量,减少计算量,防止过拟合。
Kernel Operations:
在过滤器的基础上,控制过滤器移动的步长和范围,两者结合实现局部感知。
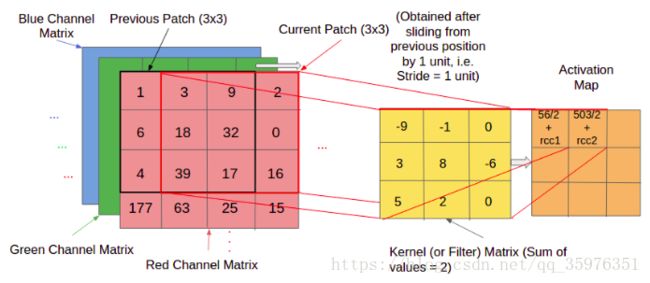
Receptive Field
感知域。由于隐藏层不是与输入层进行的全链接,因此进行了卷积操作。经过卷积后,每个神经元相当于只与前一层的部分神经元进行链接。链接的这一部分就是该神经元的感知域。左侧每个神经元的感知域是整个图片,而右侧每个神经元仅仅是感知局部。
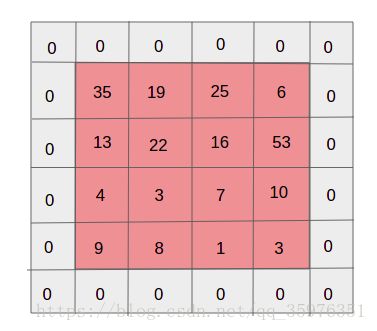
Zero-Padding
在图像的边界添加0边。最常用的情景是我们需要卷积前和卷积后的图片尺寸相同。
卷积神经网络隐藏层的种类
卷积层(Convolutional Layer):
为什么使用卷积层:
前面的描述中,我们知道CNN的一个重大的突破就是某些神经元只观测图片的局部,那么卷积就是实现这个作用。
卷积层的一般介绍:
卷积在数学上用于过滤信号,并识别信号中的模式。在卷积层中,所有的神经源使用卷积操作输入数据。对于卷积层来说,最重要的参数是过滤尺寸。假设我们有553的卷积层应用在输入尺寸为32323的尺寸的输入上,见下图。
现在让我们应用一个553的过滤器在一副图片上,并且计算卷积结果。这个卷积操作会产生一个数字作为输出,我们会在输出结果上增加一个偏置项。
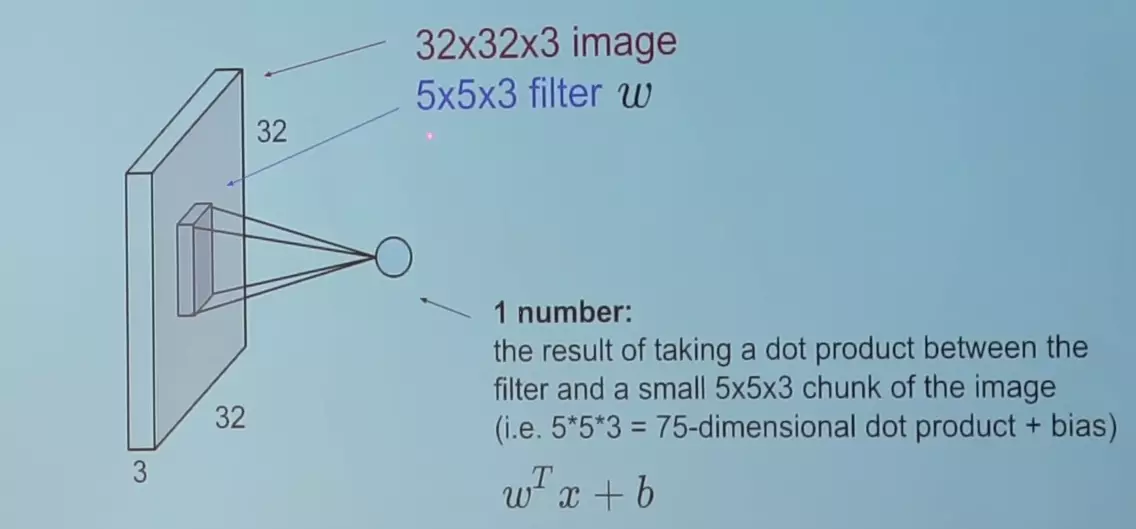
卷积的实际操作相当于一个矩阵的点积操作。同时,过滤器每次会移动一个像素的距离,有些情况下,移动的距离会多于1个像素。这个移动距离称为“stride”。
只有一个Filter的简单情况下:
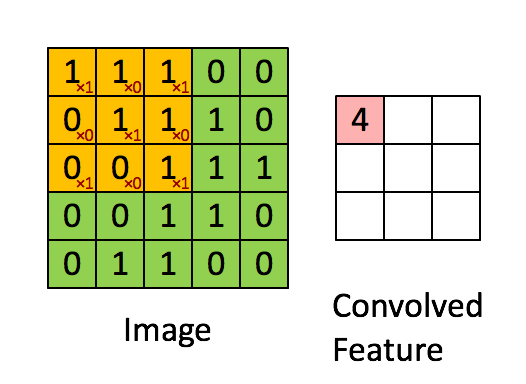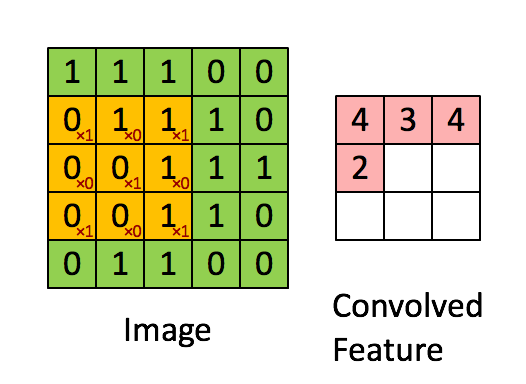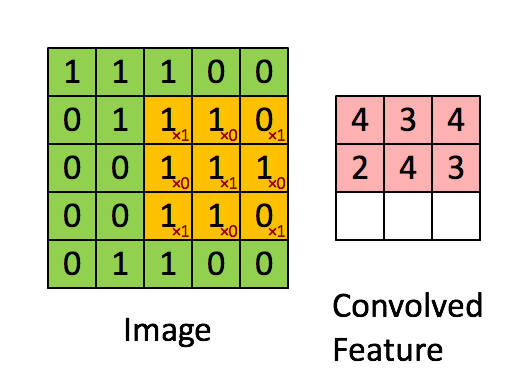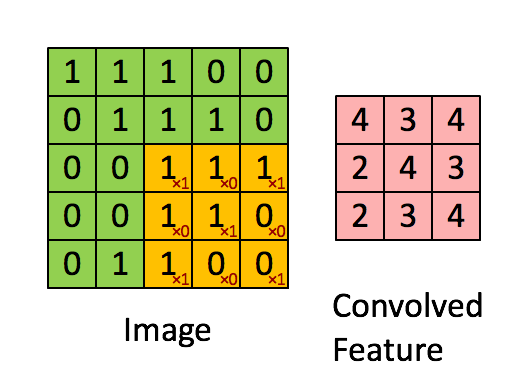
如果使用多个Filter和多个volume的话,会是这种情况,注意添加了0。
可以看到,Filter的权重是不同的,经过不同的卷积核对应的卷积后,把输入的蓝色的每一个卷积后结果再次累加,得到绿色的输出结果。
如果我们串联上述所有的输出在2D平面上,我们会得到一个2828的激活图。一般来说,我们在一个卷积层中使用不止一个过滤器。比如,如果我们使用6个过滤器,我们得到一个28286的输出。也就是说,可以添加多个过滤器,获取多个不同的卷积输出层。
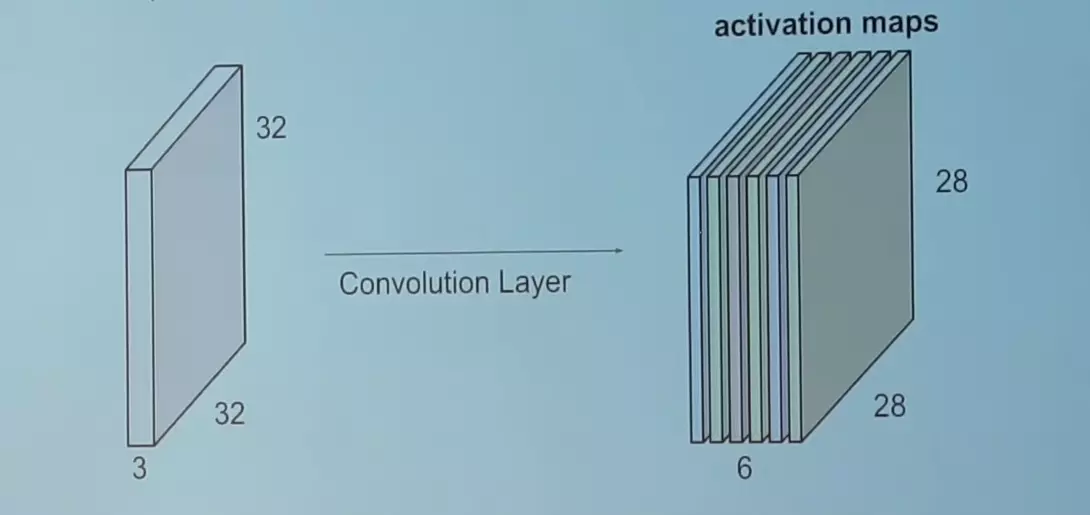
正如我们看到的,在每次卷积之后,输出的尺寸会减少。在一个有多个中间层的深神经网络中,输出会变得非常小,这可能使网络的效果不太好。因此,一个标准的操作是在输出层的边界添加0元素,这样操作后,会让输出的尺寸和输入的尺寸相等。在上面的例子中年,如果我们把32323的图片的每条边上添加2排0元素,那么或会输出32326的尺寸。假设我们的输入尺寸是 N × N N\times N N×N(仅从二维上看)的,过滤器的尺寸是 F × F F\times F F×F(仅从二维上看),使用 S S S的步长(stride),输入的层添加0边的尺寸是 P P P,那么输出尺寸是:
N − F + 2 P S + 1 \frac{N-F+2P}{S}+1 SN−F+2P+1
上述例子中:(32-5+22)/1+1=32
Tensorflow中关于卷积层的函数:
官方文档说明
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, data_format=None, name=None)
把4维的输入计算出2维的卷积。
input:格式为[batch, in_height, in_width, in_channels]。batch是一个批次训练输入的图片的个数;in_height和in_width分别是高度和宽度;in_channels是上面提到的channelfilter:滤波器,格式为:[filter_height, filter_width, in_channels, out_channels]。filter_height和filter_width分别是高度和宽度,in_channels是输入图片的channel,out_channels是自定义输出层的channel。 关于out_channels的解释,根据个人理解与这篇博客和这篇博客,可以视为输出out_channels的个数,也可以理解成前边的Filter的个数。比如下图中,Layer1中Conv到Maxpoling中,由32channel到32channel;Layer1到Layer2时,由32变成64。在这期间,相当于后面的一层与前面一层根据channel数进行一次连接操作。(下图有一个错误,全连接第一层应该是3136个神经元)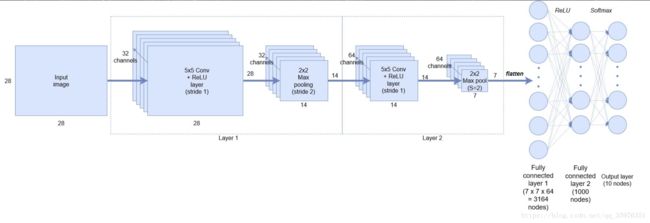
对应上面的动图,输入的channel数就是红色卷积核的行数,也是输入矩阵的个数;而输出channel个数就是红色卷积列数,也是输出矩阵的个数。strides:控制卷积操作的步长,是4维的(至于为什么4维,参照官方文档)。基本格式为:[1, stride, stride, 1],两个1不能改,stride表示移动的步长,一般是1或者2.padding: 添加0边。取值是"SAME"和"VALID"字符值,具体算法的区别参照官网use_cudnn_on_gpu:使用GPU加速,默认是True,需要安装CUDNN和 CUDAdata_format:控制数据输出格式,参照官方文档)name:可选的,表示操作名字
池化层(Pooling Layer):
为什么使用池化层:
因为一张图片,如果我们抽取出部分像素,那么一般不会影响对图片的识别。比如10001000的图片变成500500的图片,只是分辨率下降了,但是一般不影响我们对图片的观测;但是对计算机来说,却能极大减少运算量。
池化层的简介:
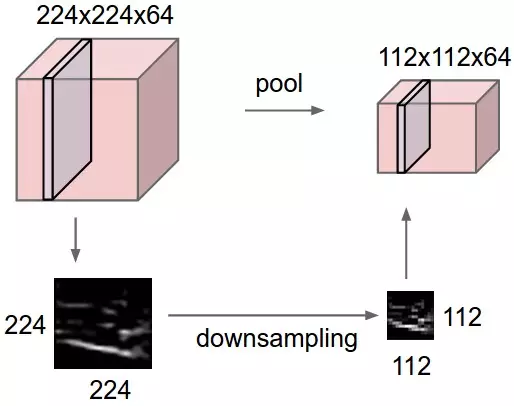
池化层的大多数情况下在卷积层后面使用,用来减少图片的空间尺寸(只是在宽和高上,不在深度上)。这减少了参数的数量,因此计算量得到了降低;同时,更少的参数会躲避“过拟合”。一般来说,最常用的是Max Pooling,即使用 F × F F\times F F×F的过滤器,并且选取过滤器内部最大的数字。如下图:

还有一种操作是Average Pooling,对过滤器内部的数字取平均值,但是这个操作不是很流行。
假设我们的输入尺寸是: w 1 × h 1 × d 1 w_1\times h_1\times d_1 w1×h1×d1,过滤器的尺寸是 f × f f\times f f×f,步长stride是 S S S,那么输出的尺寸 w 2 × h 2 × d 2 w_2\times h_2\times d_2 w2×h2×d2将会是:
w 2 = ( w 1 − f ) / S + 1 h 2 = ( h 2 − f ) / S + 1 h 2 = ( h 1 − f ) / S + 1 d 2 = d 1 w_2=(w_1-f)/S+1\\h_2=(h_2-f)/S+1\\h_2=(h_1-f)/S+1\\d_2=d_1 w2=(w1−f)/S+1h2=(h2−f)/S+1h2=(h1−f)/S+1d2=d1
最常用的池化操作是使用2*2的过滤器和步长为2的stride。正如上述公式看到的,这会使图像尺寸减少一半。比如:
Tensorflow中池化层处理函数:
tf.nn.max_pool(
value, # 输入卷积层
ksize,
strides, # 与卷积层类似
padding, # 与卷积层类似
data_format='NHWC',
name=None
)
特别说明下ksize:一般是[1,ksize,ksie,1],ksize表示池化窗口的大小,第一个1表示仅仅在每个输入上进行池化,第二个表示仅在每个输出的channel进行池化,不交叉进行。
###全连接层(Fully Connected Layer):
如果某一层的每个神经元收到了前一层的所有神经元的输入,那么这一层称为全连接层。全连接层通过矩阵乘法进行计算,计算完成后要添加偏置项。Tensorflow中没有集成全连接的函数,需要我们自己实现。
实现全连接层,需要把最后一层的多维张量进行一次flatten操作,舒展成向量的形式。Tensorflow中,借助于函数:
tf.reshape(
tensor, # 输入的张量
shape, # 输出的形状,是一个Tensor,数据类型必须是int32或者int64
name=None # 名字
)
实现。在卷积层函数说明那一节,图片上有全连接的介绍。
理解训练过程
卷积神经网络的数学模型相当于模拟一个微型的大脑,我们需要两件事情来完善这个模型:
1. 构建神经网络的架构
设计神经网络的架构是很复杂的,而且需要很高的技巧,在这方面有很多研究。这里有很多的标准架构,它们在处理一般性问题上有很好的效果,比如说:AlexNet、GoogleNet、InceptionResnet、VGG等。在初学阶段,我们只需要使用标准的网络结构即可,当我们积累了足够多的经验后,再去设计自己的结构
2. 正确处理网络权重和参数
调整最优权重一般使用梯度下降算法(Back Propagation(BP)算法和其他的一些优化方法结合),这其中涉及到梯度下降求导计算问题。对于卷积神经网络来说,这是非常复杂的,不过Tensorflow已经实现了自动化求导的过程,我们只需要调用有关的函数即可。
在训练过程中,我们需要给出梯度下降的步长(学习速率),也需要给出自己定义或者Tensorflow中集成的损失函数,算法的最终的目的是尽量减少损失函数的数值。一个最简单的损失函数是:
c o s t = 1 2 ( y a c t u a l − y p r e d i c t i o n ) T ( y a c t u a l − y p r e d i c t i o n ) cost= \frac{1}{2}(\bf{y_{actual}-y_{prediction}})^T(\bf{y_{actual}-y_{prediction}}) cost=21(yactual−yprediction)T(yactual−yprediction)
注意使用了向量化计算方式。
在训练结束后,我们需要把有关的参数存储在一个二进制文件中,该文件称为模型。我们可以使用相同架构的神经网络来加载这个模型,用于图像识别。
为了计算简单,我们不会把所有的数据一次性加载到模型中进行训练。相反的,假设我们有1600张图片,并把这1600张图片分解成每批次16或者32张,那么16或32称为batch-size; 整个训练过程需要100或者50次,每次称为一个迭代(Iteration);当所有图片都被训练过后,称为一次Epoch