深度学习回归问题--预测房价

环境使用keras为前端，TensorFlow为后端

背景：

  波士顿房价数据集统计了当时教区部分的犯罪率、房产税等共计13个指标，统计出房价，试图能找到那些指标与房价的关系。

首先加载数据集

from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) =  boston_housing.load_data()

train_data.shape
#结果为(404,13)

训练集共有404条数据，每条数据都有13个指标

准备数据

#数据标准化
#由于数据集有13个参考的维度，而这些维度的数据指标的单位是不同的，所以要把这些数据单位指标的影响去除，使数据能够在同一个量纲上进行讨论。
#而就算去除了数据单位，数据之间的关系仍在。
#这里使用的是0均值标准化，即对于输入数据的每个特征(输入数据矩阵中的列),减去特征平均值，再除以标准差，这样得到的特征平均值为0，标准差为1
#如数据为1,2,3，将1,2,3分别减去平均值得-1,0,1。-1,0,1的标准差为√2/√3,再将-1,0,1除去√2/√3,得到-√6/2,0,√6/2;-√6/2,0,√6/2的标准差
#为√((6/4 + 0 + 6/4)/3) = √1 = 1。所以经过标准化，最终得到特征平均值为0，标准差为1的标准正态分布。
mean = train_data.mean(axis=0) #axis=0表示每一列的数据
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
#用于测试数据集标准化的标准差和均值都是从训练数据上得到的，而不能使用在测试数据上计算得到的任何结果
test_data -= mean
test_data /= std
#对于train_data.mean()
#类似于
'''
import numpy as np
a = np.array([[2,3],[4,5]])
print(a)
#输出为[[2 3]
       [4 5]]
'''
'''
np.mean(a)#求所有值的均值
#输出为3.5

'''
'''
np.mean(a,axis=0)#求所有列的均值
#输出为array([3., 4.])
'''
'''
np.mean(a,axis=1)#求所有行的均值
#输出为array([2.5, 4.5])

'''

构建网络

from keras import models
from keras import layers

def build_model():
    # Because we will need to instantiate
    # the same model multiple times,
    # we use a function to construct it.
    model = models.Sequential()
    #input_shape为传入一个shape给第一层，为13行的矩阵,所以要求输入的数据为13列的矩阵
    model.add(layers.Dense(64, activation='relu',
                           input_shape=(train_data.shape[1],)))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

此网络的最后一层只有一个单元，没有激活，是线性层。所以网络可以学会预测任意范围内的值。

损失函数使用的是mse损失函数，即均方误差(MSE,mean squared error)，是预测值与目标值之差的平方。是回归问题常用的损失函数。

平均绝对误差(MAE, mean absolute error) ，是预测值与目标值之差的绝对值。若mae=0.1，则表示预测房价与实际价格平均相差100美元

K折验证

由于数据点很少，所以验证集也非常小，所以验证集的划分会产生很大的影响，难以对模型进行可靠的评估

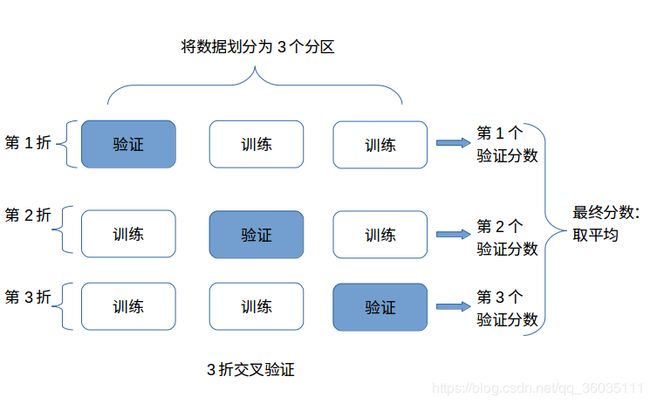
所以可以考虑使用K折交叉验证。这种方法将可用数据划分为K个分区，实例化K个相同的模型，使每个模型在K-1个分区上训练，并在剩下那个分区上进行评估。模型的验证分数等于K个验证分数的平均值，如图

K折验证code：

import numpy as np

k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []
for i in range(k):
    print('processing fold #', i)
    #准备验证数据：第k个分区的数据
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

    #准备训练数据：其他所有分区的数据
    partial_train_data = np.concatenate(
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

    # 构建已编译的模型
    model = build_model()
    #训练模型，为静默模式，即不在标准输出流输出日志信息(verbose=0),训练100轮
    model.fit(partial_train_data, partial_train_targets,
              epochs=num_epochs, batch_size=1, verbose=0)
    #在验证数据集上评估模型
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose=0)
    all_scores.append(val_mae)

最终的4次的平均值

np.mean(all_scores)
#结果为2.386301112056959

预测的价格与实际价格相差约2300美元，差距较大。

所以尝试增加训练轮次为500

num_epochs = 500
all_mae_histories = []
for i in range(k):
    print('processing fold #', i)
   
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

  
    partial_train_data = np.concatenate(
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

    model = build_model()

    history = model.fit(partial_train_data, partial_train_targets,
                        validation_data=(val_data, val_targets),
                        epochs=num_epochs, batch_size=1, verbose=0)
    mae_history = history.history['val_mean_absolute_error']
    all_mae_histories.append(mae_history)

再计算每个轮次中mae的平均值

average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

绘制验证分数

import matplotlib.pyplot as plt

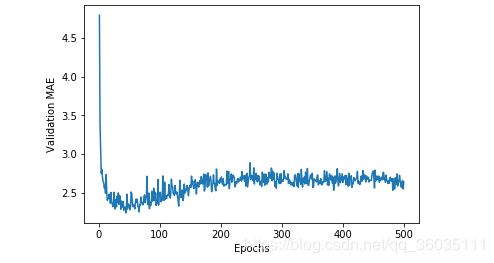
plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

def smooth_curve(points, factor=0.9):
  smoothed_points = []
  for point in points:
    if smoothed_points:
      previous = smoothed_points[-1]
      smoothed_points.append(previous * factor + point * (1 - factor))
    else:
      smoothed_points.append(point)
  return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:])

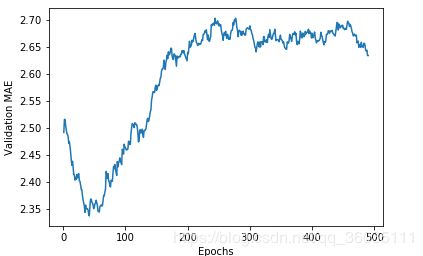
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

从图中可看出，约在70轮开始过拟合

训练最终模型

model = build_model()
model.fit(train_data, train_targets,
          epochs=70, batch_size=1, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

最终结果如下

test_mae_score
#2.3388691228978775

最终结果与实际相差2330美元左右，与之前数据相近

总结：

1.回归问题常用的损失是均方误差(mse)

2.常见的回归指标是平均绝对误差(mae)

3.如果输入数据的特征具有不同的取值范围，应该先进行预处理，对每个特征单独进行缩放

4.如果可用的数据很少，使用K折验证可以可靠地评估模型

5.如果可用的训练数据很少，最好使用隐藏层较少的小型网络，避免严重的过拟合