Tarjan算法详解

强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

Tarjan算法：求解有向图强连通分量的线性时间的算法。

Tarjan的模拟过程可参考这篇博客（写得挺详细的）

Tarjan算法是基于dfs的算法。
定义：
dfn[i] 表示 i号节点在dfs序中的位置（可以理解为dfs 第dfn[i]次到了i号点）
low[i] 表示 i号点 它能走到的dfn最小的点

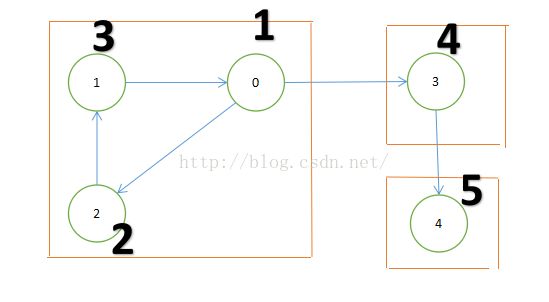
我们来模拟一个图。。

这个时候我们回头来看第二个数组要怎样操作，我们定义low【u】=min(low【u】，low【v】（即使v搜过了也要进行这步操作，但是v一定要在栈内才行）)，u代表当前节点，v代表其能到达的节点。这个数组在刚刚到达节点u的时候初始化：low【u】=dfn【u】。然后在进行下一层深搜之后回溯回来的时候，维护low【u】。如果我们发现了某个节点回溯之后的low【u】值还是==dfn【u】的值，那么这个节点无疑就是一个关键节点：从这个节点能够到达其强连通分量中的其他节点，但是没有其他属于这个强连通分量以外的点能够到达这个点，所以这个点的low【u】值维护完了之后还是和dfn【u】的值一样，口述可能理解还是相对费劲一些，我们走一遍流程图：

①首先进入0号节点，初始化其low【0】=dfn【0】=1，然后深搜到节点2，初始化其：low【2】=dfn【2】=2，然后深搜到节点1，初始化其：low【1】=dfn【1】=3；

②然后从节点1开始继续深搜，发现0号节点已经搜过了，没有继续能够搜的点了，开始回溯维护其值。low【1】=min（low【1】，low【0】）=1；low【2】=min（low【2】，low【1】）=1；low【0】=min（low【0】，low【2】）=1；

③这个时候猛然发现，low【0】==dfn【0】，这个时候不要太开心，就断定一定0号节点是一个关键点，别忘了，这个时候还有3号节点没有遍历，我们只有在其能够到达的节点全部判断完之后，才能够下结论，所以我们继续Dfs。

④继续深搜到3号节点，初始化其low【3】=dfn【3】=4，然后深搜到4号节点，初始化其：low【4】=dfn【4】=5，这个时候发现深搜到底，回溯，因为节点4没有能够到达的点，所以low【4】也就没有幸进行维护即：low【4】=dfn【4】（这个点一定是强连通分量的关键点，但是我们先忽略这个点，这个点没有代表性，一会分析关键点的问题），然后回溯到3号节点，low【3】=min（low【3】，low【4】）=4；发现low【3】==dfn【3】那么这个点也是个关键点，我们同样忽略掉。

⑤最终回溯到节点0，进行最后一次值的维护：low【0】=min（low【0】，low【3】）=0，这个时候我们猛然发现其dfn【0】==low【0】，根据刚才所述，那么这个点就是一个关键点：能够遍历其属强连通分量的点的起始点，而且没有其他点属于其他强连通分量能够有一条有向路径连到这个节点来的节点。

大家仔细理解一下这句话，因为这个点属于一个强连通分量，而且强连通分量中的任意两个节点都是互达的，也就是说强连通分量中一定存在环，这个最后能够回到0号节点的1号节点一定有机会维护low【1】，因为0号节点是先进来的，所以其low【1】的值也一定会跟着变小，然后在回溯的过程中，其属一个强连通分量的所有点都会将low【u】值维护成low【0】，所以这个0号节点就是这个关键点：能够遍历其属强连通分量的起始点而且这样的起始点一定只有一个，所以只要发现了一个这样的关键起始点，那么就一定发现了一个强连通分量。而且这个节点没有其他点属于其他强连通分量能够有一条有向路径连到这个节点来的节点：如果这样的点存在，那么这些个点应该属于同一个强连通分量。

那么综上所述，相信大家也就能够理解为什么dfn【u】==low【u】的时候，我们就可以判断我们发现了一个强连通分量了。

以上转自这里
接着看代码（他的代码有些问题，等下我会分析）

错误代码（上面那篇博客的）：

void Tarjan(int u)//此代码仅供参考  
{  
    vis[u]=1;  
    low[u]=dfn[u]=cnt++;  
    for(int i=0;i

正确的：

stack z;//这个栈很关键， 先看注释
void tarjan(int x)
{
    low[x] = dfn[x] = ++cnt;//先设初始状态
    vis[x] = 1;//x点在栈中
    z.push(x);
    for(int i = last[x]; i; i = g[i].next)
    {
        int to = g[i].to;
        if(!dfn[to])//to没有dfs过，则dfs
        {
            tarjan(to);
            low[x] = min(low[x], low[to]);
        }
        else if(vis[to]) low[x] = min(low[x], dfn[to]);
        /*如果dfs过并且to在栈中,说明to与x在同一强连通分量中。
		low[i] 表示 i号点 它能走到的dfn最小的点, 所以取min */
    }
    if(low[x] == dfn[x])
    {
        ans++;
        while(z.top()!=x)
        {
            vis[z.top()] = 0;
            z.pop();
        }
        vis[z.top()] = 0;
        z.pop();
        /*low[x] == dfn[x] 所以在x之后进入的与x构成了强联通分量
        （不懂就模拟一下）
        然后全部弹出，x也要弹出，因为点x已经dfs完了*/
    }
    return ;
}
void work()
{
    for(int i = 1; i <= n; i++)
        if(!dfn[i])
            tarjan(i);
    return ;
}

栈的操作：
不断加入点，如果当前的点够成了强连通分量， 则 栈顶到当前的点全部删掉

如果还不懂，再看一遍上面的程序，找一组小数据模拟一下。。。

为什么第一篇代码错了？

因为，那篇代码没有进栈出栈的操作，导致if(vis[v]==1)low[u]=min(low[u],low[v]) 中的if 毫无作用，但实际这个if有很大的作业（判断v与u是否在同一强连通分量中。。。）
没看懂的话，我们模拟一组数据
2 1
2 1
错误程序一开始dfs（1），dfn [1]= low[1] = 1,
然后dfs(2), low[2] = min(dfn[2], low[1]) = min(2, 1) = 1。。
就只有一个强联通分量了，但实际是两个。

接下来我们讨论一下Tarjan算法能够干一些什么：

既然我们知道，Tarjan算法相当于在一个有向图中找有向环，那么我们Tarjan算法最直接的能力就是缩点辣！缩点基于一种染色实现，我们在Dfs的过程中，尝试把属于同一个强连通分量的点都染成一个颜色，那么同一个颜色的点，就相当于一个点。比如刚才的实例图中缩点之后就可以变成这样：

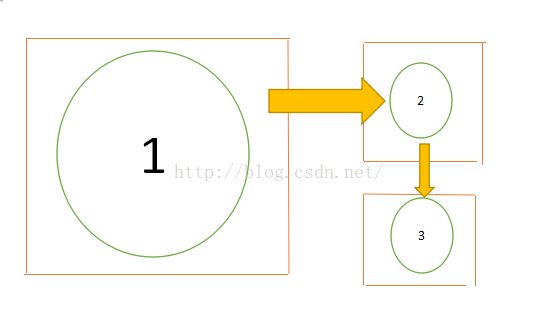
将一个有向带环图变成了一个有向无环图(DAG图)。很多算法要基于有向无环图才能进行的算法就需要使用Tarjan算法实现染色缩点，建一个DAG图然后再进行算法处理。在这种场合，Tarjan算法就有了很大的用武之地辣！

那么这个时候 ，我们再引入一个数组color【i】表示节点i的颜色，然后在Dfs过程中每一次遇到点都将点入栈，在每一次遇到关键点的时候将栈内元素弹出，一直弹到栈顶元素是关键点的时候为止，对这些弹出来的元素进行染色即可。

代码实现：

void tarjan(int x)
{
    low[x] = dfn[x] = ++cnt;
    vis[x] = 1;
    z.push(x);
    for(int i = last[x]; i; i = g[i].next)
    {
        int to = g[i].to;
        if(!dfn[to])
        {
            tarjan(to);
            low[x] = min(low[x], low[to]);
        }
        else if(vis[to]) low[x] = min(low[x], dfn[to]);
    }
    if(low[x] == dfn[x])
    {
        ans++;
        while(vis[x])
        {
            color[z.top()] = ans;
            vis[z.top()] = 0;
            z.pop();
        }
        color[z.top()] = ans;
        vis[z.top()] = 0;
        z.pop();
    }
    return ;
}
void work()
{
    for(int i = 1; i <= n; i++)
        if(!dfn[i])
            tarjan(i);
    return ;
}

例题：
洛谷 P3387 【模板】缩点
洛谷 P3388 【模板】割点（割顶）