KNN(k-nearest neighbor的缩写)最近邻算法原理详解
k-最近邻算法是基于实例的学习方法中最基本的,先介绍基于实例学习的相关概念。
基于实例的学习
- 已知一系列的训练样例,很多学习方法为目标函数建立起明确的一般化描述;但与此不同,基于实例的学习方法只是简单地把训练样例存储起来。
从这些实例中泛化的工作被推迟到必须分类新的实例时。每当学习器遇到一个新的查询实例,它分析这个新实例与以前存储的实例的关系,并据此把一个目标函数值赋给新实例。 - 基于实例的方法可以为不同的待分类查询实例建立不同的目标函数逼近。事实上,很多技术只建立目标函数的局部逼近,将其应用于与新查询实例邻近的实例,而从 不建立在整个实例空间上都表现良好的逼近。当目标函数很复杂,但它可用不太复杂的局部逼近描述时,这样做有显著的优势。
- 基于实例方法的不足
- 分类新实例的开销可能很大。这是因为几乎所有的计算都发生在分类时,而不是在第一次遇到训练样例时。所以,如何有效地索引训练样例,以减少查询时所需计算是一个重要的实践问题。
- 当从存储器中检索相似的训练样例时,它们一般考虑实例的所有属性。如果目标概念仅依赖于很多属性中的几个时,那么真正最“相似”的实例之间很可能相距甚远。
k-最近邻法
算法概述
K最近邻(K-Nearest Neighbor,KNN)算法,是著名的模式识别统计学方法,在机器学习分类算法中占有相当大的地位。它是一个理论上比较成熟的方法。既是最简单的机器学习算法之一,也是基于实例的学习方法中最基本的,又是最好的文本分类算法之一。
基本思想
如果一个实例在特征空间中的K个最相似(即特征空间中最近邻)的实例中的大多数属于某一个类别,则该实例也属于这个类别。所选择的邻居都是已经正确分类的实例。
该算法假定所有的实例对应于N维欧式空间Ân中的点。通过计算一个点与其他所有点之间的距离,取出与该点最近的K个点,然后统计这K个点里面所属分类比例最大的,则这个点属于该分类。
该算法涉及3个主要因素:实例集、距离或相似的衡量、k的大小。
一个实例的最近邻是根据标准欧氏距离定义的。更精确地讲,把任意的实例x表示为下面的特征向量:
<a1(x),a2(x),...,an(x)>
其中ar(x)表示实例x的第r个属性值。那么两个实例xi和xj间的距离定义为d(xi,xj),其中:
d(xi,xj)=∑r=1n(ar(xi)−ar(xj))2−−−−−−−−−−−−−−−−−√
有关KNN算法的几点说明:
- 在最近邻学习中,目标函数值可以为离散值也可以为实值。
- 我们先考虑学习以下形式的离散目标函数。其中V是有限集合{v1,...,vs}。下表给出了逼近离散目标函数的k-近邻算法。
- 正如下表中所指出的,这个算法的返回值f′(xq)为对f(xq)的估计,它就是距离xq最近的k个训练样例中最普遍的f值。
- 如果我们选择k=1,那么“1-近邻算法”就把f(xi)赋给(xq),其中xi是最靠近xq的训练实例。对于较大的k值,这个算法返回前k个最靠近的训练实例中最普遍的f值。
逼近离散值函数f:Ân−V的k-近邻算法
训练算法:
对于每个训练样例<x,f(x)>,把这个样例加入列表training_examples
分类算法:
给定一个要分类的查询实例xq
在training_examples中选出最靠近xq的k个实例,并用x1,....,xk表示
返回
其中如果a=b那么d(a,b)=1,否则d(a,b)=0
简单来说,KNN可以看成:有那么一堆你已经知道分类的数据,然后当一个新数据进入的时候,就开始跟训练数据里的每个点求距离,然后挑离这个训练数据最近的K个点看看这几个点属于什么类型,然后用少数服从多数的原则,给新数据归类。
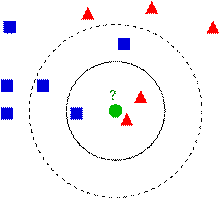
KNN算法的决策过程
下图中有两种类型的样本数据,一类是蓝色的正方形,另一类是红色的三角形,中间那个绿色的圆形是待分类数据:
如果K=3,那么离绿色点最近的有2个红色的三角形和1个蓝色的正方形,这三个点进行投票,于是绿色的待分类点就属于红色的三角形。而如果K=5,那么离绿色点最近的有2个红色的三角形和3个蓝色的正方形,这五个点进行投票,于是绿色的待分类点就属于蓝色的正方形。
下图则图解了一种简单情况下的k-最近邻算法,在这里实例是二维空间中的点,目标函数具有布尔值。正反训练样例用“+”和“-”分别表示。图中也画出了一个查询点xq。注意在这幅图中,1-近邻算法把xq分类为正例,然而5-近邻算法把xq分类为反例。
图解说明:左图画出了一系列的正反训练样例和一个要分类的查询实例xq。1-近邻算法把xq分类为正例,然而5-近邻算法把xq分类为反例。
右图是对于一个典型的训练样例集合1-近邻算法导致的决策面。围绕每个训练样例的凸多边形表示最靠近这个点的实例空间(即这个空间中的实例会被1-近邻算法赋予该训练样例所属的分类)。
对前面的k-近邻算法作简单的修改后,它就可被用于逼近连续值的目标函数。为了实现这一点,我们让算法计算k个最接近样例的平均值,而不是计算其中的最普遍的值。更精确地讲,为了逼近一个实值目标函数f:Rn⟶R,我们只要把算法中的公式替换为:
f(xq)⟵∑ki=1f(xi)k
针对传统KNN算法的改进
- 快速KNN算法。参考FKNN论述文献(实际应用中结合lucene)
- 加权欧氏距离公式。在传统的欧氏距离中,各特征的权重相同,也就是认定各个特征对于分类的贡献是相同的,显然这是不符合实际情况的。同等的权重使得特征向量之间相似度计算不够准确, 进而影响分类精度。加权欧氏距离公式,特征权重通过灵敏度方法获得(根据业务需求调整,例如关键字加权、词性加权等)
距离加权最近邻算法
对k-最近邻算法的一个显而易见的改进是对k个近邻的贡献加权,根据它们相对查询点xq的距离,将较大的权值赋给较近的近邻。
例如,在上表逼近离散目标函数的算法中,我们可以根据每个近邻与xq的距离平方的倒数加权这个近邻的“选举权”。
方法是通过用下式取代上表算法中的公式来实现:
f(xq)⟵argmaxv∈V∑i=1kwiδ(v,f(xi))
其中
wi≡1d(xq,xi)2
为了处理查询点xq恰好匹配某个训练样例xi,从而导致分母为0的情况,我们令这种情况下的f′(xq)等于f(xi)。如果有多个这样的训练样例,我们使用它们中占多数的分类。
我们也可以用类似的方式对实值目标函数进行距离加权,只要用下式替换上表的公式:
f(xq)⟵∑ki=1wif(xi)∑ki=1wi
其中wi的定义与之前公式中相同。
注意这个公式中的分母是一个常量,它将不同权值的贡献归一化(例如,它保证如果对所有的训练样例xi,f(xi)=c,那么(xq)←c)。
注意以上k-近邻算法的所有变体都只考虑k个近邻以分类查询点。如果使用按距离加权,那么允许所有的训练样例影响xq的分类事实上没有坏处,因为非常远的实例对(xq)的影响很小。考虑所有样例的惟一不足是会使分类运行得更慢。如果分类一个新的查询实例时考虑所有的训练样例,我们称此为全局(global)法。如果仅考虑最靠近的训练样例,我们称此为局部(local)法。
四、KNN的优缺点
(1)优点
①简单,易于理解,易于实现,无需参数估计,无需训练;
②精度高,对异常值不敏感(个别噪音数据对结果的影响不是很大);
③适合对稀有事件进行分类;
④特别适合于多分类问题(multi-modal,对象具有多个类别标签),KNN要比SVM表现要好.
(2)缺点
①对测试样本分类时的计算量大,空间开销大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本;
②可解释性差,无法给出决策树那样的规则;
③最大的缺点是当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进;
④消极学习方法。
五、对k-近邻算法的说明
按距离加权的k-近邻算法是一种非常有效的归纳推理方法。它对训练数据中的噪声有很好的鲁棒性,而且当给定足够大的训练集合时它也非常有效。注意通过取k个近邻的加权平均,可以消除孤立的噪声样例的影响。
问题一:近邻间的距离会被大量的不相关属性所支配。
应用k-近邻算法的一个实践问题是,实例间的距离是根据实例的所有属性(也就是包含实例的欧氏空间的所有坐标轴)计算的。这与那些只选择全部实例属性的一个子集的方法不同,例如决策树学习系统。
比如这样一个问题:每个实例由20个属性描述,但在这些属性中仅有2个与它的分类是有关。在这种情况下,这两个相关属性的值一致的实例可能在这个20维的实例空间中相距很远。结果,依赖这20个属性的相似性度量会误导k-近邻算法的分类。近邻间的距离会被大量的不相关属性所支配。这种由于存在很多不相关属性所导致的难题,有时被称为维度灾难(curse of dimensionality)。最近邻方法对这个问题特别敏感。
解决方法:当计算两个实例间的距离时对每个属性加权。
这相当于按比例缩放欧氏空间中的坐标轴,缩短对应于不太相关属性的坐标轴,拉长对应于更相关的属性的坐标轴。每个坐标轴应伸展的数量可以通过交叉验证的方法自动决定。
问题二:应用k-近邻算法的另外一个实践问题是如何建立高效的索引。因为这个算法推迟所有的处理,直到接收到一个新的查询,所以处理每个新查询可能需要大量的计算。
解决方法:目前已经开发了很多方法用来对存储的训练样例进行索引,以便在增加一定存储开销情况下更高效地确定最近邻。一种索引方法是kd-tree(Bentley 1975;Friedman et al. 1977),它把实例存储在树的叶结点内,邻近的实例存储在同一个或附近的结点内。通过测试新查询xq的选定属性,树的内部结点把查询xq排列到相关的叶结点。
Python实现KNN算法
这里实现一个手写识别算法,这里只简单识别0~9数字。
输入:每个手写数字已经事先处理成32*32的二进制文本,存储为txt文件。每个数字大约有200个样本。每个样本保持在一个txt文件中。手写体图像本身的大小是32x32的二值图,转换到txt文件保存后,内容也是32x32个数字,如下图所示。目录trainingDigits存放的是大约2000个训练数据,testDigits存放大约900个测试数据。
- 函数img2vector:用来生成将每个样本的txt文件转换为对应的一个向量
# convert image to vector
def img2vector(filename):
rows = 32
cols = 32
imgVector = zeros((1, rows * cols))
fileIn = open(filename)
for row in xrange(rows):
lineStr = fileIn.readline()
for col in xrange(cols):
imgVector[0, row * 32 + col] = int(lineStr[col])
return imgVector- 函数loadDDataSet:加载整个数据库
# load dataSet
def loadDataSet():
## step 1: Getting training set
print "---Getting training set..."
dataSetDir = './'
trainingFileList = os.listdir(dataSetDir + 'trainingDigits') # load the training set
numSamples = len(trainingFileList)
train_x = zeros((numSamples, 1024))
train_y = []
for i in xrange(numSamples):
filename = trainingFileList[i]
# get train_x
train_x[i, :] = img2vector(dataSetDir + 'trainingDigits/%s' % filename)
# get label from file name such as "1_18.txt"
label = int(filename.split('_')[0]) # return 1
train_y.append(label)
## step 2: Getting testing set
print "---Getting testing set..."
testingFileList = os.listdir(dataSetDir + 'testDigits') # load the testing set
numSamples = len(testingFileList)
test_x = zeros((numSamples, 1024))
test_y = []
for i in xrange(numSamples):
filename = testingFileList[i]
# get train_x
test_x[i, :] = img2vector(dataSetDir + 'testDigits/%s' % filename)
# get label from file name such as "1_18.txt"
label = int(filename.split('_')[0]) # return 1
test_y.append(label)
return train_x, train_y, test_x, test_y - 函数kNNClassify:实现kNN分类算法
# classify using kNN
def kNNClassify(newInput, dataSet, labels, k):
numSamples = dataSet.shape[0] # shape[0] stands for the num of row
## step 1: calculate Euclidean distance
# tile(A, reps): Construct an array by repeating A reps times
# the following copy numSamples rows for dataSet
diff = tile(newInput, (numSamples, 1)) - dataSet # Subtract element-wise
squaredDiff = diff ** 2 # squared for the subtract
squaredDist = sum(squaredDiff, axis = 1) # sum is performed by row
distance = squaredDist ** 0.5
## step 2: sort the distance
# argsort() returns the indices that would sort an array in a ascending order
sortedDistIndices = argsort(distance)
classCount = {} # define a dictionary (can be append element)
for i in xrange(k):
## step 3: choose the min k distance
voteLabel = labels[sortedDistIndices[i]]
## step 4: count the times labels occur
# when the key voteLabel is not in dictionary classCount, get()
# will return 0
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
## step 5: the max voted class will return
maxCount = 0
for key, value in classCount.items():
if value > maxCount:
maxCount = value
maxIndex = key
return maxIndex - 函数testHandWritingClass:测试函数
# test hand writing class
def testHandWritingClass():
## step 1: load data
print "step 1: load data..."
train_x, train_y, test_x, test_y = loadDataSet()
## step 2: training...
print "step 2: training..."
pass
## step 3: testing
print "step 3: testing..."
numTestSamples = test_x.shape[0]
matchCount = 0
for i in xrange(numTestSamples):
predict = kNNClassify(test_x[i], train_x, train_y, 3)
if predict == test_y[i]:
matchCount += 1
accuracy = float(matchCount) / numTestSamples
## step 4: show the result
print "step 4: show the result..."
print 'The classify accuracy is: %.2f%%' % (accuracy * 100)
相似性度量
相似性一般用空间内两个点的距离来度量。距离越大,表示两个越不相似。
作为相似性度量的距离函数一般满足下列性质:
- d(X,Y)=d(Y,X);
- d(X,Y)≦d(X,Z)+d(Z,Y);
- d(X,Y)≧0;
- d(X,Y)=0,当且仅当X=Y;
这里,X,Y和Z是对应特征空间中的三个点。
假设X,Y分别是N维特征空间中的一个点,其中X=(x1,x2,...,xn)T,Y=(y1,y2,...,yn)T,d(X,Y)表示相应的距离函数,它给出了X和Y之间的距离测度。
距离的选择有很多种,常用的距离函数如下:
1. 明考斯基(Minkowsky)距离
d(X,Y)=[∑i=1n∣xi−yi∣λ]1λ,λ一般取整数值,不同的λ取值对应于不同的距离
-
曼哈顿(Manhattan)距离
d(X,Y)=∑i=1n∣xi−yi∣,该距离是Minkowsky距离在λ=1时的一个特例
-
Cityblock距离
d(X,Y)=∑i=1nwi∣xi−yi∣,该距离是Manhattan距离的加权修正,其中wi,i=1,2,...,n是权重因子
-
欧几里德(Euclidean)距离(欧式距离)
d(X,Y)=[∑i=1n∣xi−yi∣2]12=(X−Y)(X−Y)T−−−−−−−−−−−−−−√,是Minkowsky距离在λ=2时的特例
-
Canberra距离
d(X,Y)=∑i=1nxi−yixi+yi
(6)Mahalanobis距离(马式距离)
d(X,M)=(X−M)TΣ−1(X−M)−−−−−−−−−−−−−−−−−−√
d(X,M)给出了特征空间中的点X和M之间的一种距离测度,其中M为某一个模式类别的均值向量,∑为相应模式类别的协方差矩阵。
该距离测度考虑了以M为代表的模式类别在特征空间中的总体分布,能够缓解由于属性的线性组合带来的距离失真。易见,到M的马式距离为常数的点组成特征空间中的一个超椭球面。
-
切比雪夫(Chebyshev)距离
d(X,Y)=maxi(∣xi−yi∣)
L∞=limk→∞(∑i=1k∣xi−yi∣k)1k
切比雪夫距离或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各坐标数值差的最大值。在二维空间中。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为d=max(∣x2−x1∣,∣y2−y1∣)
切比雪夫距离或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各坐标数值差的最大值。在二维空间中。以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为
d=max(|x2−x1|,|y2−y1|)
-
平均距离
daverage=[1n∑i=1n(xi−yi)2]12
消极学习与积极学习
- 积极学习(Eager Learning)
这种学习方式是指在进行某种判断(例如,确定一个点的分类或者回归中确定某个点对应的函数值)之前,先利用训练数据进行训练得到一个目标函数,待需要时就只利用训练好的函数进行决策,显然这是一种一劳永逸的方法,SVM就属于这种学习方式。 - 消极学习(Lazy Learning)
这种学习方式指不是根据样本建立一般化的目标函数并确定其参数,而是简单地把训练样本存储起来,直到需要分类新的实例时才分析其与所存储样例的关系,据此确定新实例的目标函数值。也就是说这种学习方式只有到了需要决策时才会利用已有数据进行决策,而在这之前不会经历 Eager Learning所拥有的训练过程。KNN就属于这种学习方式。 -
比较
- Eager Learning考虑到了所有训练样本,说明它是一个全局的近似,虽然它需要耗费训练时间,但它的决策时间基本为0.
- Lazy Learning在决策时虽然需要计算所有样本与查询点的距离,但是在真正做决策时却只用了局部的几个训练数据,所以它是一个局部的近似,然而虽然不需要训练,它的复杂度还是需要 O(n),n 是训练样本的个数。由于每次决策都需要与每一个训练样本求距离,这引出了Lazy Learning的缺点:(1)需要的存储空间比较大 (2)决策过程比较慢。
-
典型算法
- 积极学习方法:SVM;Find-S算法;候选消除算法;决策树;人工神经网络;贝叶斯方法;
- 消极学习方法:KNN;局部加权回归;基于案例的推理;
文献资料
[1] Trevor Hastie & Rolbert Tibshirani. Discriminant Adaptive Nearest Neighbor Classification. IEEE TRANSACTIONS ON PAITERN ANALYSIS AND MACHINE INTELLIGENCE,1996.
[2] R. Short & K. Fukanaga. A New Nearest Neighbor Distance Measure,Pro. Fifth IEEE Int’l Conf.Pattern Recognition,pp.81-86,1980.
[3] T.M Cover. Nearest Neighbor Pattern Classification,Pro. IEEE Trans,Infomation Theory,1967.
[4] C.J.Stone. Consistent Nonparametric Regression ,Ann.Stat.,vol.3,No.4,pp.595-645,1977.
[5] W Cleveland. Robust Locally-Weighted Regression and Smoothing Scatterplots,J.Am.Statistical.,vol.74,pp.829-836,1979.
[6] T.A.Brown & J.Koplowitz. The Weighted Nearest Neighbor Rule for Class Dependent Sample Sizes,IEEE Tran. Inform.Theory,vol.IT-25,pp.617-619,Sept.1979.
[7] J.P.Myles & D.J.Hand. The Multi-Class Metric Problem in Nearest Neighbor Discrimination Rules,Pattern Recognition,1990.
[8] N.S.Altman. An Introduction to Kernel and Nearest Neighbor Nonparametric Regression,1992.
[9]Min-Ling Zhang & Zhi-Hua Zhou. M1-KNN:A Lazy Learning Approach to Multi-Label Learning,2007.
[10]Peter Hall,Byeong U.Park & Richard J. Samworth. Choice of Neighbor Order In Nearest Neighbor Classification,2008.
[11] Jia Pan & Dinesh Manocha. Bi-Level Locality Sensitive Hashing for K-Nearest Neighbor Computation,2012.