NOI级别的超强数据结构——Link-cut-tree(动态树)学习小记
前言
其实LCT这种东西,我去年就接触过并且打过,只不过一直没调出来。最近优化了我那又丑又长的splay打法,并且用LCT切了道题。在此做一个小结。
简介
如果有一道题,让我们维护一棵树,支持以下操作:
1.链上求和;
2.链上求最值;
3.链上修改;
4.子树修改;
5.子树求和;
这道题用树链剖分就可以切掉了。
但如果这题是让我们支持以下操作:
1.链上求和;
2.链上求最值;
3.链上修改;
4.子树修改;
5.子树求和;
6.换根;
7.断开树上一条边;
8.连接两个点,保证连接后仍然是一棵树。
多了这三个操作的话,树链剖分就捉襟见肘了。因为我们知道,树链剖分是通过线段树维护链信息的,而线段树是静态的,不能加/减边。
这时,LCT应运而生。
LCT,也就是link cut tree的缩写。它是最常见的一种解决动态树问题的工具。顾名思义,动态树就是会动的树,也即会加/减边的树。不过说它是树也不准确,因为它可以是一片森林。
思想
树链剖分有重链和轻边。我们的LCT也一样,分实(重)边和虚(轻)边。我们知道,一个节点最多连出一条向儿子的实边,因此实边会聚集成链。根据树链剖分的思想,我们需要用一种数据结构来维护实边组成的链。树链剖分使用了线段树来维护,但线段树显然很静态。
我们思考可以使用能动态的平衡树——splay!
至于为什么不用treap,据说是因为LCT的时间复杂度需要势能分析。(我不会告诉你们我不会treap)
概念
Preferred Child:偏爱儿子,偏爱儿子与父亲节点同在一棵Splay中,一个节点最多只能有一个偏爱儿子(注意,LCT的偏爱儿子与树链剖分的重儿子迥乎不同,后者是点数最大的儿子,而前者则是随便的);
Preferred Edge:实边,连接父亲节点和偏爱儿子的边;
Preferred Path:偏爱路径,由实边及实边连接的节点构成的链;
Auxiliary Tree:辅助树,由一条偏爱路径上的所有节点所构成的Splay称作这条链的辅助树。每个点的键值为这个点的深度,即这棵Splay的中序遍历是这条链从链顶到链底的所有节点构成的序列。辅助树的根节点的父亲指向链顶的父亲节点,然而链顶的父亲节点的儿子并不指向辅助树的根节点。
注意:实边连起来会组成偏爱路径,偏爱路径之间没有公共点。
树链剖分的重链是固定的,但是lct的偏爱路径是可以改变(动态)的。
若一个不在偏爱路径上的点也视为一条没有实边的偏爱路径,那么偏爱路径之间是用虚边连接的。
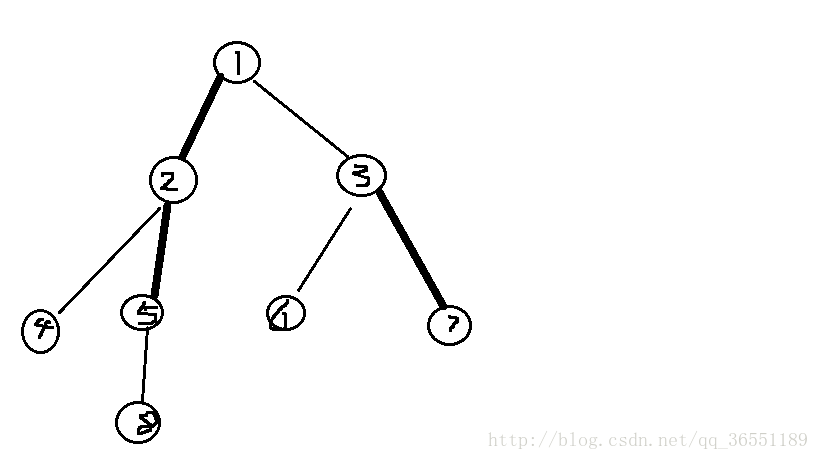
如图,加粗的是重边,1->5是一条重链,3->7是一条重链。
基础操作:so、link、if_root
so(x)是查询x为其父亲节点的左儿子还是右儿子;link(y,x,d)表示从y向x连一条实边,其中x会变为y的d儿子(注意,此处的link并不是简介中的操作8,纯粹只是连实边);if_root(x)是判断x是否为其splay上的根。
bool so(int x)
{
return son[fat[x]][1]==x;
}
void link(int f,int x,bool d)
{
son[fat[x]=f][d]=x;
}
bool if_root(int x)
{
return !fat[x]||son[fat[x]][so(x)]!=x;
}核心操作:access
什么是access?英文好一点可以读懂是“访问”。
access(x)其实就是访问某个节点,似乎没有太特殊的意义。
至于这个操作为什么要命名为access,我也不知道。
access(x)的真正含义:让x节点不含偏爱儿子,同时x到根节点所有边均为实边。
算法的流程如下:
因为x节点不能含偏爱儿子,先将x旋至其所在splay的根,然后断开右子树(变为虚边)。
接着我们顺着偏爱路径往上爬,每遇到一条虚边,我们同样把虚边连向的节点y旋至y所在splay的根然后断开y的右子树(使y不含有偏爱儿子),并把x所在splay接在y的右子树(把虚边改为实边)。
这就完成了access。
void access(int y)
{
int x=0;
while(y)//y不为整棵LCT的根
{
splay(y);//将y旋至其所在splay的根
link(y,x,1);//把x所在splay接在y的右子树,这样同时也会冲掉y原来的右子树
x=y;
y=fat[y];
}
}重要操作:makeroot
makeroot(x)即为将x变为整棵LCT的根。
算法流程如下:对x进行access,然后观察,我们发现虚边子树会随着依附子树一起选择;而x到根的路径则会在同一棵splay里,且x是深度最大的点。
而换根之后改变了什么?x到目前根节点路径上这条偏爱路径被反了过来!
那我们只需要打一个翻转标记即可。
来自某Chair大佬的友情提醒:“注意打标记在点x时,x的左右儿子已经交换了,不然在一些极复杂的题可能会GG。”
容易看出,makeroot操作的复杂度与access一致。
void makeroot(int x)
{
access(x);
splay(x);
fan(x);
}操作7和操作8:link和cut
有了access和makeroot,link(两棵树接在一起)和cut(断开树上一条边)变得很容易操作。
link:先将x变为根,然后直接连轻边上去
cut:假如要断开x和x父亲y间的边,则对y进行access,然后切开x到y的轻边
容易看出,这两个操作复杂度与access复杂度一致。
链信息维护
灵活掌握access,就能进行很好的链信息维护。
树上的任意一条路径,在以某个节点为根后都将变成一条树链。
我们用splay维护重链信息,然后进行链信息查询时,例如查询u到v,我们可以让u作为根,然后access节点v,于是u到v的路径此时变成了一条重链,那么也就是所有点在一颗splay里,然后这条路径不就任你摆布了?
我们发现,access是一个基础,所有LCT的操作复杂度基本都与access复杂度一致!
所以,access复杂度是多少呢?
access复杂度
我们知道,splay的每次操作,均摊时间复杂度是 O(log2n) O ( l o g 2 n ) (虽然我还不会势能分析),那么access估计比splay慢。但是你可以从一些大佬写的国家队论文得出每次access的均摊时间复杂度和splay一致。至于证明,有待理解。
对于边权
我们知道,绝大多数树上乱搞的题都是带权的。但是splay不能维护边权——splay中的边会随旋转变换。那么,这里有一个很好的思路:将边看作一个点,将其连向其两端的点,然后将边权记录在表示边的点那里。这样我们就能藐视那些带权的树上乱搞的题了。
正确性
学到这里,我们知道,LCT的形态并非一成不变的。它甚至还会随时将某些虚边变为实边,将某些实边变为虚边,将其中某棵splay整个翻转从而改变许多点的键值。那么它为什么能保持求得的答案正确呢?
我的理解是:你无论如何虚实变换、翻转splay,所有点的相对键值是一成不变的,于是如果原本x到y的路径中没有点z,操作完以后x到y的路径中也不可能出现点z。
例题
1.【ZJOI2008】树的统计
Problem
一棵树上有n个节点,编号分别为1到n,每个节点都有一个权值w。
我们将以下面的形式来要求你对这棵树完成一些操作:
I. CHANGE u t : 把结点u的权值改为t
II. QMAX u v: 询问从点u到点v的路径上的节点的最大权值
III. QSUM u v: 询问从点u到点v的路径上的节点的权值和
注意:从点u到点v的路径上的节点包括u和v本身
Hint
对于100%的数据,保证1<=n<=30000,0<=q<=200000;中途操作中保证每个节点的权值w在-30000到30000之间。
Solution
这题本来是树链剖分的模板题,我们把它加进例题里面,用LCT切掉它。
由于实在水满而溢,所以直接上代码:
Code
#include 2.【JZOJ3754】【NOI2014】魔法森林
Problem
给出一个n(≤50000)个节点m(≤100000)条边的无向图,每条边有两个权值ai,bi(1≤ai,bi≤50000)。求一条从点1到点n的路径,使得经过的边的maxai+maxbi最小。输出这个最小值。
Solution
LCT维护最小生成树。
鉴于有两个权值的限制,我们就考虑消除掉ai带来的影响。
按ai为关键字,将所有边从小到大排序。我们每次枚举一个maxai,将所有可行但却未尝插入过的边插进LCT里。由于我们现在已消除了ai的限制,我们只需用LCT维护bi即可。
当然,我们知道这么插可能会插出一个环,那就不属于LCT可维护的范围。
那么,每次我们要插一条从x到y的边时,我们就先把x变为根,access一下y,然后如果它们原本就是相连的,此刻它们就会在同一棵splay里面,我们想怎么搞就怎么搞;反之,则不在同一棵splay里面。若它们原本不相连,我们直接连边即可;否则,我们须查询一下x到y的maxbi,与此边的bi比较一下:若后者更小,我们就删掉那一条最大的边,连上后者。
对于答案的更新,我们同上一段的方法判断1到n是否相连,若相连则查询1到n的maxbi,加上当前枚举的maxai与答案取min即可。
Code
#include void push(int x)
{
if(!f[x].tag)return;
if(A)f[A].tag=!f[A].tag,swap(son[A][0],son[A][1]);
if(B)f[B].tag=!f[B].tag,swap(son[B][0],son[B][1]);
f[x].tag=0;
}
void up(int x)
{
f[x].max=f[x].w;
f[x].mi=x;
if(A&&f[A].max>f[x].max)f[x].max=f[A].max,f[x].mi=f[A].mi;
if(B&&f[B].max>f[x].max)f[x].max=f[B].max,f[x].mi=f[B].mi;
}
bool so(int x)
{
return son[fat[x]][1]==x;
}
void link(int f,int x,bool d)
{
if(x)
son[fat[x]=f][d]=x;
else son[f][d]=0;
}
bool if_root(int x)
{
return !fat[x]||son[fat[x]][so(x)]!=x;
}
void rotate(int x)
{
if(!x)return;
int y=fat[x],z=fat[y],k=so(x),b=son[x][!k];
link(y,b,k);
if(!if_root(y))
link(z,x,so(y));
else fat[x]=z;
link(x,y,!k);
up(y);
up(x);
}
void clear(int x)
{
d[++d[0]]=x;
while(!if_root(x))d[++d[0]]=x=fat[x];
while(d[0])push(d[d[0]--]);
}
void splay(int x)
{
clear(x);
for(int f=fat[x];!if_root(x);rotate(x),f=fat[x])
rotate(!if_root(f)?so(x)==so(f)?f:x:0);
}
void splay(int x,int y)
{
clear(x);
for(int f=fat[x];f!=y;rotate(x),f=fat[x])
rotate(fat[f]!=y?so(x)==so(f)?f:x:0);
}
void access(int y)
{
int x=0;
while(y)
{
splay(y);
link(y,x,1);
x=y;
y=fat[y];
}
}
void fan(int x)
{
f[x].tag=!f[x].tag;
swap(A,B);
}
void makeroot(int x)
{
access(x);
splay(x);
fan(x);
}
void splay1(int x)
{
clear(x);
for(int f=fat[x];!if_root(f);rotate(x),f=fat[x])
rotate(!if_root(fat[f])?so(x)==so(f)?f:x:0);
}
void cut(int x,int y)
{
makeroot(x);
access(y);
splay(x);
splay(y,x);
son[x][so(y)]=fat[y]=0;
}
void Link(int x,int y)
{
makeroot(x);
fat[x]=y;
}
int main()
{
scanf("%d%d",&n,&m);
fo(i,1,m)
{
scanf("%d%d%d%d",&a[i].x,&a[i].y,&a[i].a,&a[i].b);
if(a[i].x==a[i].y)i--,m--;
}
sort(a+1,a+m+1);
ans=1<<30;
i=0;
fo(maxai,a[1].a,a[m].a)
{
while(i1].a==maxai)
{
i++;
x=a[i].x;
y=a[i].y;
b=a[i].b;
makeroot(x);
access(y);
splay(x);
splay1(y);
if(fat[y]==x)
{
ys=son[y][!so(y)];
ma=f[ys].max;
mi=f[ys].mi;
if(ma<=b)continue;
cut(a[mi-n].x,mi);
cut(mi,a[mi-n].y);
}
f[n+i].w=b;
up(n+i);
Link(x,n+i);
Link(n+i,y);
}
makeroot(1);
access(n);
splay(1);
splay1(n);
if(fat[n]==1)ans=min(ans,f[son[n][!so(n)]].max+maxai);
}
if(ans==1<<30)ans=-1;
printf("%d",ans);
} 3.【JZOJ3766】【BJOI2014】大融合
Problem
给出N(≤100000)个点和Q(≤100000)个操作,操作有两种:
A x y 表示在x和y之间连一条边。保证之前x和y是不联通的。
Q x y 表示询问经过(x,y)这条边的简单路径数。保证x和y之间有一条边。
Solution
LCT维护子树大小。
显然在一棵树中,经过(x,y)的简单路径数等于x那边的子树大小*y那边的子树大小。
对于插入(x,y)这条边,我们makeroot(x和y),然后从x向y连一条虚边。makeroot(x)是为了让x不再有父亲节点,好连;makeroot(y)是为了我们直接将size[y]+=size[x],方便更新,而不必一直往y的祖先走更新。
对于询问答案,我们用之前的方法将x搞到LCT的根节点,将y旋至x的下方,那么y那边的子树大小即为size[y],x那边的子树大小即为size[x]-size[y]。
而通过这题我们也可见一斑,在用LCT维护子树信息时,必须要连从虚边连出去的准子节点一同记录上。
Code
#include