模型评估与选择(中篇)-ROC曲线与AUC曲线
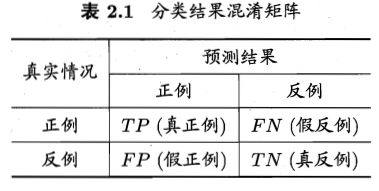
以二分类问题为例进行说明。分类结果的混淆矩阵如下图所示。
假设,现在我们用某一算法h对样本进行二分类(划分为正例、反例)。由于算法可能与理想方法存在误差,因此在划分结果中,划分为正例的那部分样本中,可能存在正例,也可能存在反例。同理,在划分为反例的那部分样本中,也可能存在这样的误差。因此,我们需要定义一些指标来衡量我们的算法的好坏程度。下面是两个是目前常用的指标——查准率、查全率。
查准率P定义为:
查全率R定义为:
P-R曲线,即基于这两个指标对算法进行直观衡量。
下面根据我的理解,谈一下P-R曲线是如何做出来的。
假设,我们的数据集包含n个样本 x1,x2,…,xn ,那么经过算法 h 处理,得到一组数值 h(x1),h(x2),…,h(xn) 。我们将这组值从高到低进行排列,假设排列的顺序就是 h(x1),h(x2),…,h(xn) ,其中 h(xn) 是算法认为最有可能为正例的样本,排在后面的 h(x1) ,是算法认为最不可能为正例的样本。有了排序结果,我们还要定义一个阈值 p0 。在二分类中,高于阈值 p0 被我们认为是正例,低于阈值 p0 的,认为是反例。
假设,我们将阈值设得很高,开始时,只认为 xn 是正例(此时只有 h(xn)>p0 ),其他结果都是反例。那么我们可以计算出一组P、R数值。之后,通过不断降低阈值 p0 的设定,使得被算法判定为正例的样本,从只有 {xn} ,到 {xn,xn−1} , {xn,xn−1,xn−2} ,直至包含所有样本 {xn,xn−1,…,x1} 。此时可以得到n组不同的P、R值。将查准率P作为横轴,查全率R作为纵轴,在坐标轴上绘制出这些P-R数组,再连成曲线,即可得到相应的P-R曲线图。

从图上所示,不同的算法,对应着不同的P-R曲线。如图所示,我们有A,B,C三条曲线。通常,我们认为如果一条曲线甲,能够被另一条曲线乙包住,则认为乙的性能优于甲。因为如果我们的算法h是最接近真实算法的条件下,在不断调整阈值 p0 过程中,在某一个 p∗0 之前,所有判定为正例的样本的实际标签也是正例(每个样本有两个标签,一个是真实的,一个是算法判定的),因此查准率P应该保持在100%,也就是1.0的位置,这种算法下的 h ,必然能够包括住其他所有曲线。在 p∗0 之后,也可以看出,理想曲线必然包含其他算法 hi 的P-R曲线。
在图2.3上,就是曲线B的性能要高于曲线C。但是A和B发生了交叉,所以不能判断出A、B之间哪个算法更优。
比较两个分类器好坏时,显然是查得又准又全的比较好,也就是的PR曲线越往坐标(1,1)的位置靠近越好。因此,在图上标记了“平衡点(Break-Even Point,简称 BEP )”。它是“查准率=查全率”时的取值,同时也是我们衡量算法优劣的一个参考。
ROC曲线
roc曲线:受试者操作特征(Receiver Operating Characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。
对于0,1两类分类问题,一些分类器得到的结果往往不是0,1这样的标签,如神经网络,得到诸如0.5,0,8这样的分类结果。这时,我们人为取一个阈值,比如0.4,那么小于0.4的为0类,大于等于0.4的为1类,可以得到一个分类结果。同样,这个阈值我们可以取0.1,0.2等等。取不同的阈值,得到的最后的分类情况也就不同。
如下面这幅图:
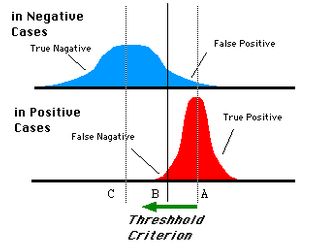
蓝色表示原始为负类分类得到的统计图,红色为正类得到的统计图。那么我们取一条直线,直线左边分为负类,右边分为正,这条直线也就是我们所取的阈值。
阈值不同,可以得到不同的结果,但是由分类器决定的统计图始终是不变的。这时候就需要一个独立于阈值,只与分类器有关的评价指标,来衡量特定分类器的好坏。
还有在类不平衡的情况下,如正样本90个,负样本10个,直接把所有样本分类为正样本,得到识别率为90%。但这显然是没有意义的。
如上就是ROC曲线的动机。
关于两类分类问题,分类混淆矩阵如下:

于是我们得到四个指标,分别为真正例,假正例;假反例,真反例。
ROC空间将假正例率(False Positive Rate, 简称FPR)定义为 X轴,真正例率(True Positive Rate, 简称TPR)定义为 Y 轴。这两个值由上面四个值计算得到,公式如下:
TPR:在所有实际为正例的样本中,被正确地判断为正例之比率。
FPR:在所有实际为反例的样本中,被错误地判断为正例之比率。
放在具体领域来理解上述两个指标。
如在医学诊断中,判断有病的样本。
那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。
而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。
不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
我们以FPR为横轴,TPR为纵轴,得到如下ROC空间。
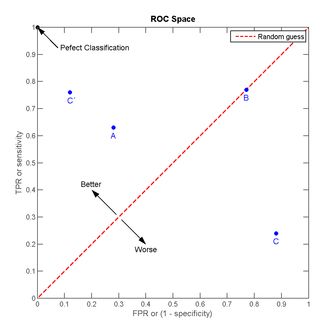
我们可以看出,左上角的点 (TPR=1,FPR=0) ,为完美分类,也就是这个医生医术高明,诊断全对。点 A(TPR>FPR) ,医生A的判断大体是正确的。中线上的点 B(TPR=FPR) ,也就是医生B全都是蒙的,蒙对一半,蒙错一半;下半平面的点 C(TPR<FPR) ,这个医生说你有病,那么你很可能没有病,医生C的话我们要反着听,为真庸医。
上图中一个阈值,得到一个点。现在我们需要一个独立于阈值的评价指标来衡量这个医生的医术如何,也就是遍历所有的阈值,得到ROC曲线。
还是一开始的那幅图,假设如下就是某个医生的诊断统计图,直线代表阈值。我们遍历所有的阈值,能够在ROC平面上得到如下的ROC曲线。
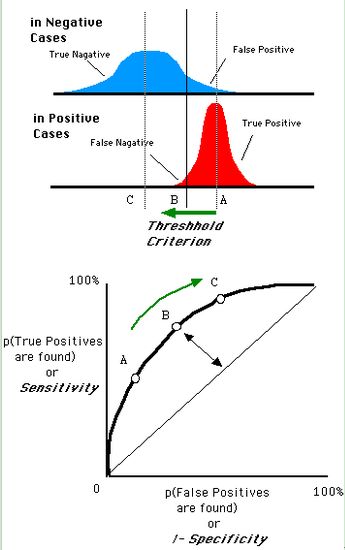
曲线距离左上角越近,证明分类器效果越好。
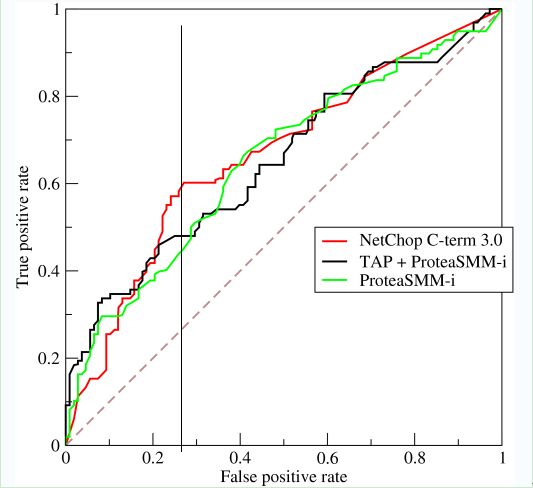
如上,是三条ROC曲线,在0.23处取一条直线。那么,在同样的低FPR=0.23的情况下,红色分类器得到更高的PTR。也就表明,ROC越往上,分类器效果越好。我们用一个标量值AUC来量化他。
附加说明:
从表2.1可以看到,真正例率和假正例率的分母,就是真实的正例个数,和反例个数。对一组数据 D 来说,假设其中有 m+ 个正例, m− 个反例,那么ROC图上,真正例率轴上的单位刻度应该是 1m+ ,假正例率轴上的单位刻度是 1m− 。(这里对应的是离散的情况,也就是图2.4 b锯齿状图的情况)
在某一算法 h 作用下,假设当前阈值 p0 下的TPR,FPR数值对在图上坐标是 (x,y) ,改变阈值后,后面一个样本被判为正例(参考ROC曲线图做法),当这个是真正例时,TP=TP+1,但是分母没有变(因为分母是真实的正例数目,真正例增加一个,必然意味着假反例减少一个),所以
绘制出如图2.4(b)所示的近似ROC曲线,绘图的过程十分简单:
给定 m+ 个正例和 m− 个反例,根据学习其预测结果对样例进行排序,然后把分类阈值设为最大,即把所有的样例均预测为反例,此时真正例率和假正例率都为0,在坐标 (0,0) 出标记一个点。然后将分类阈值依次设为每个样例的预测值,即依次将每个样例划分为正例。设前有一个标记点坐标为 (x,y) ,当前若为真正例,则对应标记点的坐标为 (x,y+1m+) ;当前若为假正例,则对应标记点的坐标为 (x+1m−,y) ,然后用线段链接相邻点即得。
也就是书上说的,此时的数值对为 (x,y+1m+)。 同理可以得到新增的预测正例是假正例的情况。
因此,ROC曲线是一个单调曲线。

从图上可以看出来,有限样本下ROC曲线从左往右,每次新增的数据点只有两种情况,或者向右一格,或者向上一格。
多个实例概率/得分相同
还需要考虑特殊情况:如果一个分类器打分结果中,有多个实例得分是一样的情况下, ROC 曲线要怎么画?比如现在有10个实例得分相同,其中6个是正例,4个是反例。
对这10个实例采用不同的具体排序方式,ROC路线是不一样的(红色点代表排在这10个实例之前的那个实例):

上图中对应两种排序方式:把所有正例排在前面;把所有反例排在前面。对于其他混合排序的情况,其路线都落在这个矩形内部。ROC曲线应该表示分类器的期望性能,也就是对角线。
AUC(Area Under ROC Curve)
在两个分类器的ROC曲线交叉的情况下,无法判断哪个分类器性能更好,这时可以计算曲线下面积AUC,作为性能度量。
现在得到分类器的ROC曲线了,怎么计算AUC呢?
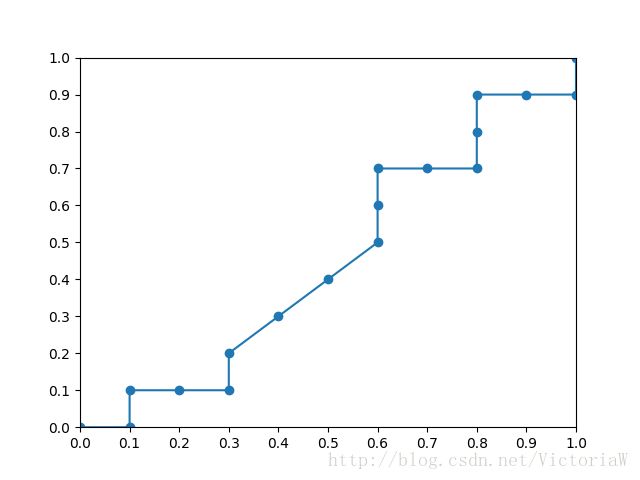
ROC曲线下方由矩形和梯形组成。因此,AUC的面积可以这样算:
AUC值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
AUC的物理意义
假设分类器的输出是样本属于正类的socre(置信度),则AUC的物理意义为,任取一对(正、负)样本,正样本的score大于负样本的score的概率。
关于损失公式的理解
在ROC图上,关于损失的定义是书中的公式2.21:

排序损失的计算公式(2.21)计算的是:对所有正例,得分比其高的反例数之和,并用 m+ m− 进行归一化。
对于得分和该正例相同的反例,数量需要除以2。
ROC曲线中,每遇到一个正例向上走一步,每遇到一个反例向右走一步。对于所有的正例,其横坐标所代表的步数就是得分比其高的反例数。我们修改ROC空间的坐标,对横坐标乘以 m− ,对纵坐标乘以 m+ ,在这个空间中每一步的刻度为1。
比如,上图中蓝色的线表示ROC曲线。根据这个曲线,我们可以知道正反例顺序:(反,正,[正,正,反],反,正,…)。其中,[]括起来的实例分数相同。对第一个正例,对应的区域1,区域1的面积表示排在其前面的反例数。
第二个正例和第三个正例是特殊情况,它们和一个反例得分是相同的。我们把这种情况一般化,假设有p个正例和q个反例的得分相同,那么有斜线对应的三角形的面积为 q2∗p ,这和公式(2.21)中的相应的情况吻合。
所以有
,左右两边同时除以 m+m− ,得到公式(2.22)。
为什么使用Roc和Auc评价分类器
既然已经这么多标准,为什么还要使用ROC和AUC呢?因为ROC曲线有个很好的特性:当测试集中的正负样本的分布变换的时候,ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡,即正负样本比例差距较大,而且测试数据中的正负样本也可能随着时间变化。下图是ROC曲线和Presision-Recall曲线的对比:
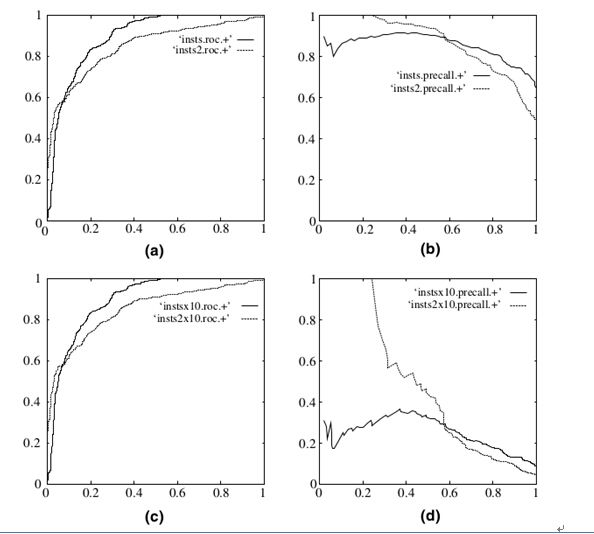
在上图中,(a)和(c)为Roc曲线,(b)和(d)为Precision-Recall曲线。
(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果,(c)(d)是将测试集中负样本的数量增加到原来的10倍后,分类器的结果,可以明显的看出,ROC曲线基本保持原貌,而Precision-Recall曲线变化较大。
iso-performance直线
ROC曲线的一个优点就是,它和测试样本的类别分布于与误分类代价无关,即无论测试样本的正反例比例如何变化、无论误分类代价如何变化,分类器的ROC曲线都是不变的。一个指定的(类别分布,误分类代价)称为一个operating condition。
假设现在指定测试样本中正例所占比例为 p(+) ,反例所占比例为 p(−) ,有 p(−)=1−p(+) 。另外,误分类代价 C(+|−) 和 C(−|+) ,分别表示实际为反例但预测成正例的代价和实际为正例但预测成反例的代价。这样得到一个operating condition,根据这个operating condition我们可以通过以下公式计算出一个值:
以 S 为斜率,在ROC空间上通过平移可以得到很多条直线,称为iso-performance直线。每条直线上的所有点对应的分类器有相同的期望代价;并且越靠近左上角的iso-performance直线,对应的分类器性能越好。
主要参考博客:
周志华《机器学习》笔记:2、模型评估与选择
wiki:ROC曲线
【西瓜书】周志华《机器学习》学习笔记与习题探讨(二)②
分类器性能指标之ROC曲线、AUC值
ROC曲线与AUC
- 西瓜书《机器学习》阅读笔记3——Chapter2_ROC曲线
- 西瓜书《机器学习》课后答案——Chapter2
排序不分先后,都是大神。