sklearn机器学习：PCA在人脸识别，降噪，手写数字案例中的使用

使用sklearn进行PCA降维之前还是需要知道PCA与SVD的知识的，移步主成分分析与奇异值分解。接下来称为一个调包侠加调参侠，对于原理基本不会说什么。依次学习以下内容。

1. PCA中的重要参数与使用PCA进行降维
2. PCA中的SVD以及一些接口的使用
3. 人脸识别案例
4. 降噪案例
5. PCA对手写数据集的降维

一、PCA中的重要参数与使用PCA进行降维

在数据预处理与特征工程部分，提到过一种重要的特征选择方法：方差过滤。如果一个特征的方差很小，则意味着这个特征上很可能有大量取值都相同（比如90%都是1，只有10%是0，甚至100%是1），那这一个特征的取值对样本而言就没有区分度，这种特征就不带有有效信息。从方差的这种应用就可以推断出，如果一个特征的方差很大，则说明这个特征上带有大量的信息。因此，在降维中，PCA使用的信息量衡量指标，就是样本方差，又称可解释性方差，方差越大，特征所带的信息量越多的表现可能会因此受影响。

下面使用鸢(yuan 第一声)尾花数据集来使用sklearn中的PCA

#高维数据的可视化
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import pandas as pd

iris = load_iris()
#iris.data.shape
x = iris.data   #(150,4)   特征矩阵
y = iris.target   #标签，3种鸢尾花类别
pca = PCA(n_components=2) #保留两个特征
x_dec = pca.fit_transform(x) #拟合并导出新的特征矩阵
x_dec.shape   #输出(150, 2)

实例化对象那步pca = PCA(n_compinents=2) 其中参数是指定降到多少维，这里是二维，鸢尾花数据集是4维的，继续上面的，降到2维那么就可以进行可视化了

plt.scatter(x_dec[y==0,0],x_dec[y==0,1],label=iris.target_names[0])
plt.scatter(x_dec[y==1,0],x_dec[y==1,1],label=iris.target_names[1])
plt.scatter(x_dec[y==2,0],x_dec[y==2,1],label=iris.target_names[2])
plt.title("PAC OF IRIS")
plt.legend()
plt.show()

可视化的样子如下

显然，簇的分布是很明显的，这时候不管是使用KNN或者随机森林等都不容易分错，准确率基本都能达到95%以上，所以说即使降到2维了也不会影响模型效果。

来看一下PCA的属性.explained_variance_，.explained_variance_ratio_

对于参数n_components有多种类型取值，可以是整数，表示降维后特征的数量；可以是[0,1]的小数，表示希望保留的信息量百分比；可以是字符类型"mle"，此时会自选时候的整数值；可以直接使用PCA(k)的形式也行；甚至可以不填，不填的话默认是min(x.shape)，由于一般是特征数量小于样本数量，所以结果通常是特征数量。

#n_components不填的话默认是min(x.shape)，由于一般是特征数量小于样本数量，所以结果通常是特征数量
pca = PCA()
x_def = pca.fit_transform(x)
pca.explained_variance_ratio_

输出：array([0.92461872, 0.05306648, 0.01710261, 0.00521218])
补充：容易看出来第一个特征（特征向量）几乎包含了所有的原始信息，如果维度巨多比如成百上千，也可以发现是前几个特征几乎包含了所有的元素信息，所以通常取前K个特征就行。我觉得自己表达的不清楚，具体的，PCA推导中最后得到的对角化的矩阵对角线元素均为各个特征值，特征值从上到下是递减排列的，而且降的特别快，如果觉得稀里糊涂，一定要看主成分分析与奇异值分解

#极大似然估计自选超参数   选择的新特征数量是3 
pca = PCA(n_components="mle")
x_mle = pca.fit_transform(x)
x_mle.shape,pca.explained_variance_ratio_

输出：((150, 3), array([0.92461872, 0.05306648, 0.01710261]))

#按照信息量占比选择超参数
pca = PCA(n_components=0.95)
x_ratio = pca.fit_transform(x)
x_ratio.shape,pca.explained_variance_ratio_

输出：((150, 2), array([0.92461872, 0.05306648]))

二、PCA中的SVD

使用PCA进行降维的时候是需要计算协方差矩阵$X{X}^T$的，其中$X=(x_{ij}{)}_{m\times n}$表示特征矩阵，这个矩阵的计算量是非常大的，sklearn中会使用SVD了来帮助计算，在主成分分析与奇异值分解中说过了其实可以根据PCA的中的一些计算得到SVD中的三个矩阵的。这里就不继续说了，实际上sklearn中是使用了算法得到了$k\times n$维度的矩阵$V_{k\times n}$的，然后$X\ast V^T$得到$m\times k$的新特征矩阵，特征数即$k$。关于这个$V$是可以直接通过属性获得的,大致流程如下。

#PCA中的SVD在transform过程之后，fit中奇异值分解
#的结果除了V(k,n)以外，就会被舍弃，而V(k,n)会被保存在属性components_ 当中，可以调用查看。
pca = PCA(2).fit(x)
pca.components_ ,pca.components_.shape #k×n ->  2×4  x*V^T -> 4×2  2表示新特征数量

输出

(array([[ 0.36138659, -0.08452251,  0.85667061,  0.3582892 ],
    [ 0.65658877,  0.73016143, -0.17337266, -0.07548102]]), (2, 4))

三、案例：人脸识别来看降维后的V的信息保存

#人脸识别案例
from sklearn.datasets import fetch_lfw_people
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt

faces = fetch_lfw_people()
faces.data.shape,faces.images.shape  #62*47=2924，像素 前者是2维数组后者是3维数组

输出：((13233, 2914), (13233, 62, 47))

figs,objs = plt.subplots(3,5
                        ,figsize=(8,5)
                        ,subplot_kw={"xticks":[],"yticks":[]} #不显示坐标轴
                       )
for i,obj in enumerate(objs.flat):#或者直接使用faces.images[i]
    obj.imshow(faces.data[i].reshape(62,47),cmap="gray")

来看原始数据的输出

现在我们进行降维，使用fit后得到的矩阵$V$来画图

#提取新特征空间   降维
x = faces.data
pca = PCA(200).fit(x)
V = pca.components_
#V.shape   #输出(200, 2914)  k=200,n=2914
figs,objs = plt.subplots(2,5,figsize=(8,5),subplot_kw={"xticks":[],"yticks":[]})
for i,obj in enumerate(objs.flat):
    obj.imshow(V[i,:].reshape(62,47),cmap="gray")

再来看画出的图像

比起降维前的数据，新特征空间可视化后的人脸非常模糊，这是因为原始数据还没有被映射到特征空间中。但是可以看出，整体比较亮的图片，获取的信息较多，整体比较暗的图片，却只能看见黑漆漆的一块。在比较亮的图片中，眼睛，鼻子，嘴巴，都相对清晰，脸的轮廓，头发之类的比较模糊。

这说明，新特征空间里的特征向量们，大部分是"五官"和"亮度"相关的向量，所以新特征向量上的信息肯定大部分是由原数据中和"五官"和"亮度"相关的特征中提取出来的。到这里，我们通过可视化新特征空间V，解释了一部分降维后的特征：虽然显示出来的数字看着不知所云，但画出来的图表示，这些特征是和”五官“以及”亮度“有关的。这也再次证明了，PCA能够将原始数据集中重要的数据进行聚集

我们学到了神奇的接口inverse_transform，可以将我们归一化，标准化，甚至做过哑变量的特征矩阵还原回原始数据中的特征矩阵，这几乎在向我们暗示，任何有inverse_transform这个接口的过程都是可逆的。PCA应该也是如此。在sklearn中，我们通过让原特征矩阵X右乘新特征空间矩阵V(k,n)来生成新特征矩阵X_dr，那理论上来说，让新特征矩阵X_dr右乘V(k,n)的逆矩阵 ，就可以将新特征矩阵X_dr还原为X。那sklearn是否这样做了呢？下面通过人脸识别来看看

#人脸识别案例
from sklearn.decomposition import PCA
from sklearn.datasets import fetch_lfw_people
import numpy as np
import matplotlib.pyplot as plt

faces = fetch_lfw_people()
x = faces.data
pca = PCA(200)
x_face = pca.fit_transform(x)
print(x_face.shape)
x_inverse = pca.inverse_transform(x_face)
print(x_inverse.shape)

输出

(13233, 200)
(13233, 2914)

从输出来看，确实是还原成了2914维，那么就画出来看

figs, objs = plt.subplots(2,10,figsize=(10,2.5),subplot_kw={"xticks":[],"yticks":[]})
for i in range(10):
    objs[0,i].imshow(x[i].reshape(62,47),cmap="gray")
    objs[1,i].imshow(x_inverse[i].reshape(62,47),cmap="gray")

对比一下，一个是原始数据得到的人脸，一个是降维后使用接口inverse_transform还原回去的数据，得到的人脸是非常相似的，虽然后者有点模糊。

这说明，inverse_transform并没有实现数据的完全逆转。这是因为，在降维的时候，部分信息已经被舍弃了，X_face中往往不会包含原数据100%的信息，所以在逆转的时候，即便维度升高，原数据中已经被舍弃的信息也不可能再回来了。所以，降维不是完全可逆的。但是同时也说明了，使用200维度，的确保留了原数据的大部分信息，所以图像看起来，才会和原数据高度相似，只是稍稍模糊罢了。

四、使用PCA进行降噪

降维的目的之一就是希望抛弃掉对模型带来负面影响的特征，而我们相信，带有效信息的特征的方差应该是远大于噪音的，所以相比噪音，有效的特征所带的信息应该不会在PCA过程中被大量抛弃。inverse_transform能够在不恢复原始数据的情况下，将降维后的数据返回到原本的高维空间，即是说能够实现”保证维度，但去掉方差很小特征所带的信息“。利用inverse_transform的这个性质，我们能够实现噪音过滤。

#案例  用PCA做噪音过滤
from sklearn.datasets import load_digits
dig = load_digits()
dig.data.shape,dig.images.shape

输出 ： ((1797, 64), (1797, 8, 8))

#定义画图方法
def draw_img(data):
    figs, objs = plt.subplots(2,10,figsize=(10,2.5),subplot_kw={"xticks":[],"yticks":[]})
    for i,obj in enumerate(objs.flat):
        obj.imshow(data[i].reshape(8,8),cmap="binary")

查看一下

现在来为数据加上噪音

#为数据加上噪音  在指定的数据集中，随机抽取服从正态分布的数据 两个参数，分别是指定的数据集，
#和抽取出来的正太分布的方差
noisy = np.random.normal(dig.data,2)
draw_img(noisy)

明显的能看到打了严重的码，背景尤其黑

现在来对具有噪音的数据进行降维，然后还原。

#降维 之后还原   清楚
pca = PCA(0.8)
x_dr = pca.fit_transform(noisy)
x_inverse = pca.inverse_transform(x_dr)
draw_img(x_inverse)

相比上一个图，是不是要清晰一点了呢。

五、PCA对手写数据集的降维

#PCA对手写数字数据集的降维 
import pandas as pd
data = pd.read_csv("D:/digit recognizor.csv")
data.shape

输出：(42000, 785)

x = data.iloc[:,1:]
y = data.iloc[:,0]
pca = PCA().fit(x)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel("dimention")
plt.ylabel("explained variance ratio")
plt.show()

从图中可以发现，当维度在100的时候可解释方差贡献率就很大了，那么我们从1-100中选一个最合适的。使用学习曲线来求超参数k，还是先确定大致范围最后再确定具体指

# 确定大致范围
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier as RFC
x = data.iloc[:,1:]
y = data.iloc[:,0]
scores = []
for i in range(1,101,10):
    x_tr = PCA(i).fit_transform(x)
    score = cross_val_score(RFC(n_estimators=10,random_state=20),x_tr,y,cv=5).mean()
    scores.append(score)
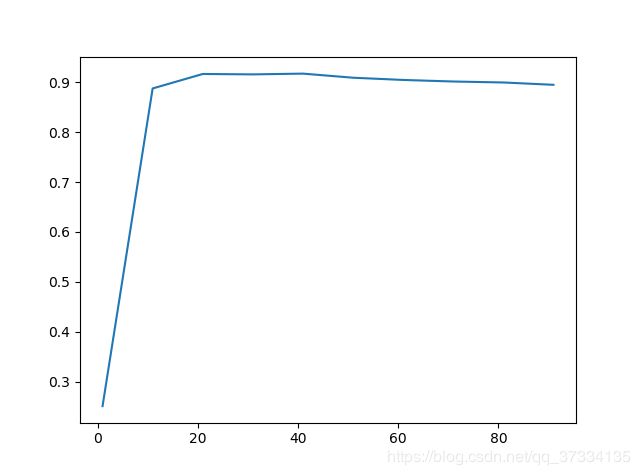
plt.plot(range(1,101,10),scores)
plt.show()  

发现k=20左右模型的效果最好，那么进一步确定具体的值

#确定范围

from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv("D:/digit recognizor.csv")
x = data.iloc[:,1:]
y = data.iloc[:,0]
scores = []
for i in range(15,30):
    x_tr = PCA(i).fit_transform(x)
    score = cross_val_score(RFC(n_estimators=10,random_state=20),x_tr,y,cv=5).mean()
    scores.append(score)
plt.plot(range(15,30),scores)
plt.show()

从图中可以看到k=25的时候，模型效果最好

x_tr = PCA(25).fit_transform(x)
cross_val_score(RFC(n_estimators=10,random_state=20),x_tr,y,cv=5).mean()

输出：0.9195949043467323
跟之前使用的特征工程的时候的效果0.96xxx相比，效果不是很好，调下参数n_estimators

x_tr = PCA(25).fit_transform(x)
cross_val_score(RFC(n_estimators=100,random_state=20),x_tr,y,cv=5).mean()

输出：0.9460957505533008

效果变好了，但是还是比0.96差不少，也许调参能使得模型效果上去，但是考虑到这里特征只有25个，那么使用KNN就不会那么慢了，使用换个KNN的模型来跑

from sklearn.neighbors import KNeighborsClassifier as KNN
x_tr = PCA(25).fit_transform(x)
cross_val_score(KNN(),x_tr,y,cv=5).mean()

输出：0.9703568517177686

精确度一下就上去了，那么就使用KNN而不使用随机森林了。