【常见笔试面试算法题12】动态规划算法案例分析
学习交流加
- 个人qq:
1126137994- 个人微信:
liu1126137994- 学习交流资源分享qq群:
962535112
文章目录
- 1、暴力搜索方法
- 2、记忆搜索方法
- 3、动态规划方法
- 4、各种动态规划方法案例总结:
给定数组arr,arr中所有数都为正数,且不重复,每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个正整数aim代表要找的钱数,求换钱有多少种方法?
这道题可以用暴力搜索,记忆搜索,动态规划,状态继续化简后的动态规划方法等四种方法!
在面试中出现类似的题目,优化轨迹高度类似!
1、暴力搜索方法
下面先看这道题的暴力搜索方法的过程:

我们认为使用0张5元,让剩下的货币值arr[10,25,1],去组成剩下的钱的过程是一个递归的过程。
同理使用1张5元。2张5元…都会有一个递归的过程!
定义一个递归数组:int p1(arr,index,aim),它的意思是如果用arr[index…N-1]这些面值的钱组成aim,返回总的方法数!!!
public int coins1(int[] arr,int aim)
{
if(arr==null||arr.length==0||aim<0)
return 0;
return process1(arr,0,aim);
}
public int process1(int[] arr,int index,int aim)
{
int res =0;
if(index==arr.length)
res = aim==0?1:0;
else
{
for(int i=0;arr[index]*i<=aim;i++) //类似于0张5元到200张5元循环组成aim
res += process1(arr,index+1,aim-arr[index]*i);
}
return res;
}
如果已经使用0张5元和1张10元的情况下,后续还需要求p1(arr,2,990)
2:表示剩下钱为arr[2,3]即为arr{25,1}
990:表示要找的剩余的钱数
当使用2张5元和0张10元的情况下,后续还是要求p1(arr,2,990)
这样的重复计算,在暴力搜索中,是非常多的,这会导致暴力搜索的时间复杂度非常高!!!
2、记忆搜索方法
暴力搜索之所以效率低,是因为每次计算后都没有把计算所得结果保存起来,下次递归后还是要重新计算。
而且我们发现在暴力搜索方法中有以下现象:
arr使用不便,index和aim始终在变化。可以让p(index,aim)来代替递归过程

还需要新加一个二维数组用于保存每一次递归的结果!

代码如下:
public int coins2(int[] arr,int aim)
{
if(arr==null||arr.length==0||aim<0)
return 0;
int[][] map = new int[arr.length][aim+1];
return process2(arr,0,aim,map);
}
public int process2(int[] arr,int index,int aim,int[][] map)
{
int res =0;
if(index==arr.length)
res = aim==0?1:0;
else
{
int mapValue = 0;
for(int i=0;arr[index]*i<=aim;i++) //类似于0张5元到200张5元循环组成aim
{
mapValue = map[index+1][aim-arr[index]*i];
if(mapValue!=0)
res += mapValue==-1?0:mapValue;
else
res += process2(arr,index+1,aim-arr[index]*i,map);
}
}
map[index][aim]=res==0?-1:res;
return res;
}
3、动态规划方法
如上图所示,dp[i][j] 表示使用arr[0…i] 货币的情况下,组成钱数j有多少种方法。上图第一列为1代表钱数为0,每一种货币都可以组成0(0乘以任意面值的货币)。
需要一行一行的计算,从上到下,从左到右,从子问题,到整个问题,最终最右下角的值,也就是dp[N-1][aim]就是我们要求的值:
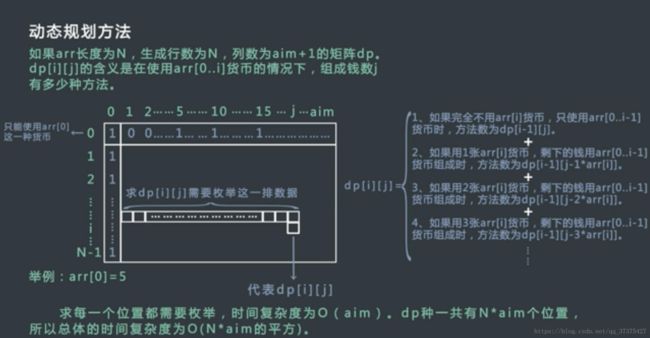
要求dp[i][j],需要枚举它上一行左边的所有值(dp[i-1][1~j])
面试题:
有数组penny,penny中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim(小于等于1000)代表要找的钱数,求换钱有多少种方法。
给定数组penny及它的大小(小于等于50),同时给定一个整数aim,请返回有多少种方法可以凑成aim。
测试样例:
[1,2,4],3,3
返回:2
class Exchange {
public:
int countWays(vector<int> penny, int n, int aim) {
// write code here
int dp[n][aim+1];
//矩阵初始化
for(int i=0;i<n;i++)
{
for(int j=0;j<aim+1;j++)
{
dp[i][j]=0;
}
}
//初始化第一行数值
for(int j=0;j<aim+1;j++)
{
if(j%penny[0]==0)
dp[0][j]=1;
}
//初始化第一列数值
for(int i=0;i<n;i++)
{
dp[i][0]=1;
}
//求其他行数值
for(int i=1;i<n;i++)
{
for(int j=1;j<aim+1;j++)
{
for(int k=0;(j-k*penny[i])>=0;k++)
{
//根据上面分析的公式
dp[i][j] += dp[i-1][j-k*penny[i]];
}
}
}
return dp[n-1][aim];
}
};
4、各种动态规划方法案例总结:
我们上述所讲的动态规划方法其实是还可以经过优化的!!!
下面先来卡一个例子:
案例1
给定一个矩阵m,从左上角开始,每次只能向右或者向下走,最后到达右下角的位置,路径上所有的数字累加起来就是路径和,返回所有的路径中,最小的路径和,如果给定的路径如下图,则最小的路径和应该为1,3,1,0,6,1,0这条路径,返回最小值为:12

假设矩阵m的大小为M*N,行数为M,列数为N,生成大小和m一样的矩阵dp,行数为M,列数为N,dp[i][j]的值等于从左上角,也就是(0,0)
走到(i,j)位置的最小路径和。
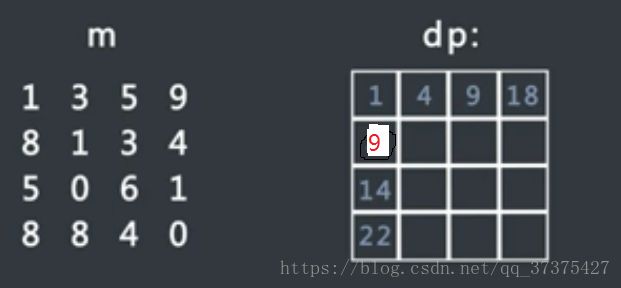
那么除了第一行和第一列的值,其他部分的值为(只能是从上面过来,或者从左边过来):
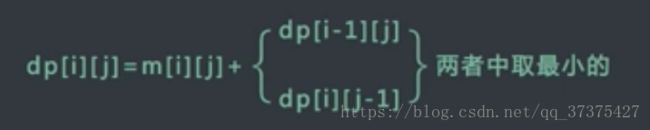
那么我们就可以先从左到右先计算每一行的值,然后从上到下计算每一列的值,最后最右下角的值,就是我们要返回的值了:
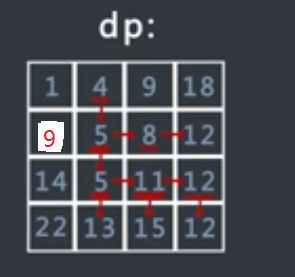
那么矩阵最右下角的值就是我们需要返回的值!!!
下一篇文章,将针对上述几个案例的具体算法题,进行编程验证!!!